Ax=0的系数矩阵A的行向量和解向量的关系
对于齐次线性方程组
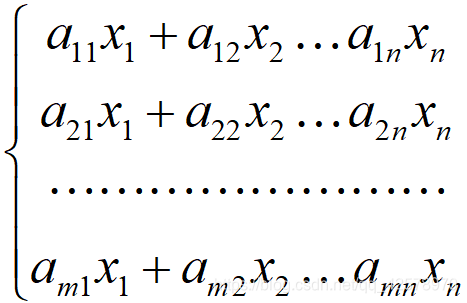
有解β=[b1,b2...bn]
记行向量αi=[ai1,ai2...ain]
则有
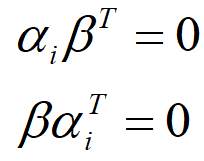
可见,以解向量作为行向量得到的新的方程组,解向量为A的行向量
例:
已知两个方程四个未知量的齐次线性方程组的通解为x=k1[1,0,2,3]T+k2[0,1,-1,1],求原齐次线性方程组
记x=k1+k2
,则有A[
,
]=0。两边同时求转置得
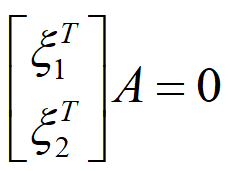
即以原方程组得基础解析作为新的方程组的系数矩阵的行向量,求解新的方程组,因此得到

求得新方程组解为k1[-2,1,1,0]T+k2[-3,-1,=,1]T
所以原方程为
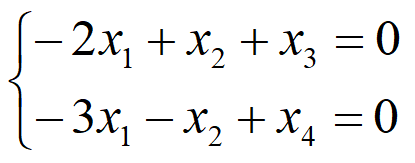
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!