[论文阅读]Color2Gray :Salience-Preserving Color Removal
《计算机图形与图像处理》课程阅读论文——Color2Gray :Salience-Preserving Color Removal
Amy A. Gooch, Sven C. Olsen, Jack Tumblin, and Bruce Gooch. 2005. Color2Gray: salience-preserving color removal. In ACM SIGGRAPH 2005 Papers (SIGGRAPH ’05). Association for Computing Machinery, New York, NY, USA, 634–639.
Abstract
当彩色图像转换成灰度图像时,在视觉上会丢失重要的图片特征。论文提出了通过尝试保留彩色图像中重要的特征来减少其丢失的算法:Color2Gray。
算法的基本思想:
在色度平面(chrominance plane)进行有符号的色度距离计算,将原始图像(source image)的色度和亮度变化映射到灰度图像中以创建保留彩色图像显著特征的目
标图像。
算法主要包括三个步骤:
1.将输入的RGB图像转换到感知均匀(perceptually uniform)的;
- L表示图形的亮度,范围从0到100,0表示黑色,100表示白色。L的值越大亮度越高。
- a表示从绿色到红色的分量,数值从负到正对应颜色从绿到红,例如-128……+127
- b表示从蓝色到红色的分量,数组从负到正对应颜色从蓝到黄,例如-128……+127
- 感知均匀:当Lab数值的变化幅度一样,给人带来视觉上的变化幅度相差不大
2.使用相邻像素色度差异(chrominance differences)和亮度差异(luminance differences)创建目标灰度图像差异(grayscale target differences);
3.将其转化为优化问题:根据原图像的色度变化有选择地调节灰度表示。
Introduction
1.若数字图像仅被看做是光学记录,那么灰度图像仅需要使用平坦光谱相应(flat spectral response)记录其光强度。但是我们希望数字图像能保留一些有意义的视觉体验,即使是在灰度图像上。
2.仅通过近似光谱均匀性构建彩色图像的灰度映射是严重不足的,因为仅有色度差异的单色视觉线索会丢失。

3.视觉科学家认为,人类视觉系统并不能感知绝对的值,相反,色度和亮度感知是基于相对评估的,在某种程度上是由于早期视觉处理阶段的细胞中心-周围组织( center-surround organization)。
Related Work
1.传统的将RGB图像转换成灰度图像的方法:点乘、加权和-->将三维颜色空间映射到一维空间。

2.彩色图像到灰度图像的转换是一个维度降低问题(dimensionality reduction problem)。
- PCA(principal component analysis)
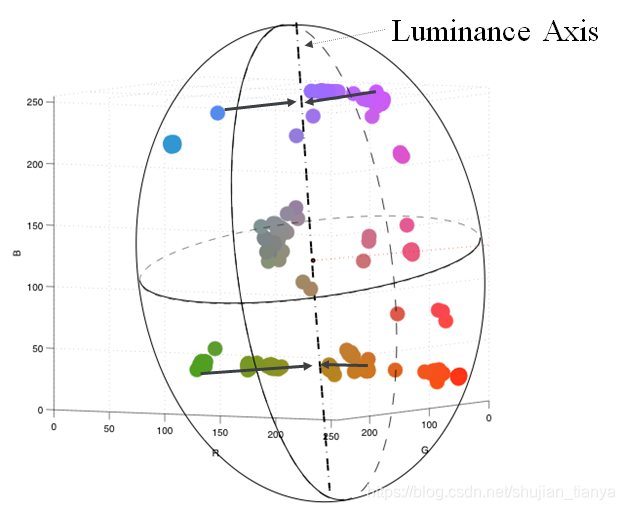
- 计算颜色空间的椭球体-->是适合所有图像颜色值组成的点的最小二乘解法。
- 可以将图像中的颜色值投影到由椭球体主轴定义的亮度轴(luminance axis)上。
- PCA的有效性取决于颜色空间(color space)。
- 主轴和副轴的比例越大,就越有可能为不同的颜色创建不同的灰度值。
- Space-filling curves
- 在颜色空间中创建簇,并且使用空间填充曲线(space-filling curves)3维颜色空间的1维参数。
Algorithm-->Color2Gray
1.基本思路
(1)将输入的RGB图像转换到感知均匀(perceptually uniform)的颜色空间-->,因为其欧氏距离与感知差异性密切相关;
(2)结合颜色差异(color differences),即亮度和色度差异计算目标差异(target differences);
对于像素i和周围(neighbor)像素j:
使用有符号距离标量δ-->亮度和色度差异
灰度图像j-->表征灰度值差异(grayscale difference),即目标差异(target differences)
目的:找到最优的g使得接近δ
(3)使用最小二乘法(a least squares optimization)有选择性地调整原图像的亮度差异以影响原图像的色度差异。
2.计算目标差异(target differences)
- 在
空间:
- Luminance difference:
- the
channel difference:
- the
channel difference:
- chrommatic difference vector:
- Luminance difference:
- 引入参数θ:
- 划分
的色度平面(chrominance plane),并且决定色度的差异是否会使得原图像亮度差异加深或减轻。
定义为θ相对于
的轴的归一化向量
- 划分


- 引入参数α:
控制应用于原图像亮度值的色度变化量
下图中参数α取值分别为5,10,25

- 引入参数μ:控制像素的相邻像素尺寸(neighborhood size)
- 目标差异(tatgrt differences)
3.解决优化问题
使用共轭梯度法(conjugate gradient iterations)最小化目标函数f(g):
移动像素:
由于f(g)是凸函数,存在多个全局最小解
Conclusion
1.算法的性能
- 解决优化问题的代价与邻域K成正比:对于S*S的图像,若邻域为整张图像,时间复杂度为
;若邻域为μ*μ,时间复杂度为
- 当邻域为整张图片时,算法处理时间
100*100:12.7s
150*150:65.6s
200*200:204.0s
2.局限性
-
在将具有大范围色度梯度进行映射到可区分的灰度图像时表现不佳

- 对于高动态场景,特别是自然场景,算法不能提供大的提升
3.结果展示

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!