matlab starcat_非刚性三维形状匹配中基于谱分析的形状描述符综述
非刚性三维形状匹配是图形学中的重要问题, 是形状识别[、形状检索[、形状配准[、形状分割[等工作的研究基础.同时, 非刚性形状匹配也为三维可视化[、生物计算[、人脸识别[、医学图像处理[等应用领域提供了坚实的理论依据.在上述研究中, 非刚性三维形状检索与非刚性三维形状匹配是两个非常相似却不相同的研究问题.非刚性三维形状检索的主要思想是:首先, 将非刚性三维形状库中的所有形状映射到特征空间中, 计算所有形状的特征值并添加索引; 其次, 根据用户的需求设置检索阈值, 并选择合适的相似度计算方法; 最后, 提取出满足阈值的形状, 并按照相似度降序输出形状[.而非刚性三维形状匹配研究的是形状相似性问题:同样将待匹配的形状映射到特征空间中, 选择形状的局部特征、全局特征或者两者的结合代替待匹配的形状; 然后选择某种代价函数或者距离函数度量特征, 并将特征之间的度量值作为非刚性三维形状匹配度.可将其概括为两个关键步骤:(1)提取形状上有效的形状描述符; (2)选择合适的相似度度量.
本文综述了非刚性三维形状匹配中基于谱分析的形状描述符.对于刚性三维形状匹配, 目前已有大量的研究成果[是最常用的三维形状匹配算法.ICP将形状上采样点的空间位置作为形状描述符, 通过多次迭代最小化源形状和目标形状采样点之间的空间距离, 实现刚性三维形状匹配.然而, ICP采用人为设置的迭代次数作为迭代终止条件, 导致算法容易陷入局部最优.此外, 对于有拓扑噪声的形状, 仅用空间位置作为形状描述符, 无法实现非刚性三维形状的高精度匹配.因此, 研究者需提取更加有效的形状描述符用于三维形状匹配.形状描述符是一种描述形状语义信息和几何信息的方法, 有时候也被称为某种算子, 研究者通过选择合适的形状描述符, 可以实现非刚性三维形状的高效匹配.常用的形状描述符一般包括4类:基于形状表面特征的描述符、基于形状统计特征的描述符、基于形状拓扑的描述符以及基于谱分析的形状描述符, 本文重点综述了基于谱分析的形状描述符.
第1类形状描述符致力于描述形状表面的特征及其在全局欧氏变换下的不变性.尺度不变特征变换(scale invariant feature transform, 简称SIFT)描述符[是其中应用最广的描述符, SIFT于1999年由Lowe等人提出, 被用于检测和描述图像中的局部特征, 并在2005年由Mikolajczy等人证明其具有很强的鲁棒性[.之后, 许多研究者也在此研究的基础上引入隐马尔可夫模型、核判别分析及测地线圆环等方法对其进行不断改进, 提高了SIFT的实时性及鲁棒性[描述了形状表面上图像中的线条, 同时存储每个点相对其他点位置的分布, 并给出形状上点的局部上下文信息, 在一定的图像区域内将点云分布转化为二维自旋图, 执行三维形状的表面匹配.为了分析有特殊铰链和关节的三维分子形状, Feng等人提出了一种基于节点感知的三维形状描述符[, 该描述符由形状边界上任意点的局部形状半径变化的信息编码定义, 用于描述有关节的三维形状.积分不变量(integral invariant)[由离散网格上顶点的几何特征定义, 例如曲率、测地线积分等, 该描述符描述了形状上的纹理特征而非几何特征.与此类似的还有Tombari等人提出的一种局部描述符——CSHOT描述符[, 该描述符通过匹配形状的特征点获得点对点的对应, 主要用于三维形状表面匹配、目标识别等.
第2类形状描述符基于对形状统计特征的描述, 主要描述形状的全局属性.Osada等人[在2002年提出了形状分布(shape distribution, 简称SD)描述符, 其算法步骤为:(1)在形状上选择合适的欧式度量函数, 如D1距离(测量形状上某个中心点到其他任意点的距离)、D2距离(测量形状上任意两点间的距离)以及D3距离(测量形状上任意3点组成区域面积的平方根)等, [使用基于D1距离改进的测地距离分布直方图作为新的形状描述符.测地距离是欧式空间中的直线段在黎曼流形上的推广, 具有等距不变性, 测地距离定义了曲面上两点间的最短距离[.测地距离不仅具有局部最短性, 还含有其他丰富的几何信息, 但当两点间的曲面部分发生缺失或者有缝隙时, 测地距离会因为联通路径不能通过而发生改变, 对拓扑变化鲁棒性不足.此后, 其他的工作也对此进行了改进, 但始终无法克服测地距离对拓扑变化的敏感性[.基于形状统计特征的形状描述符继承了统计学中统计量的稳定性, 在描述性状特征时鲁棒性较高, 很适用于分子形状比较(molecular shape comparison, 简称MSC)或者三维关节变形形状.Liu等人使用内部距离形状签名(inner distance shape signature, 简称IDSS)描述了三维分子形状, 并计算了IDSS直方图之间的度量作为三维分子形状间的相似度[.在此基础上, Liu等人基于可见性图提出一种新的内积距离计算方法, 计算了有关节的三维体模型的内部距离, 其对关节变形形状发生拓扑变化鲁棒, 能够很好地描述三维关节变形形状[.
图 1
Fig. 1
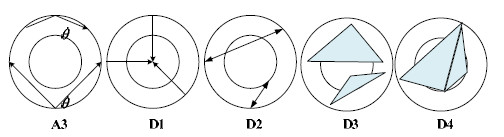
Fig. 1 Five distances defined in shape distribution
图 1 形状分布中定义的5种距离
第3类描述符基于对形状拓扑结构的特征提取, 该类描述符将三维形状匹配问题转换成其拓扑结构匹配问题, 应用两个形状拓扑结构的匹配结果作为形状的匹配结果.三维形状的拓扑结构精确地描述了形状的全局和局部几何形态特征, 并且保留了形状的层次结构.具有代表性的两类描述符分别是基于Reeb图理论的描述符和基于形状的骨架线理论的描述符,
图 2
Fig. 2
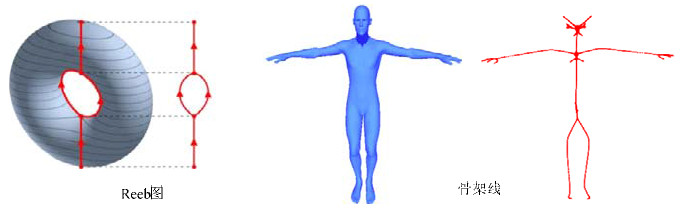
Fig. 2 Diagram of Reeb graph and skeleton with different shapes
图 2 不同形状Reeb图与骨架线图示
Reeb在1946年基于形状的拓扑结构提出了Reeb图的概念, 其具体步骤为:首先, 在三维形状的顶点上定义连续光滑函数f:M→R; 其次, 根据形状的顶点坐标计算顶点处的函数值, 并将顶点进行分类; 最后, 根据顶点分类结果将形状M映射为Reeb图R, 函数值相同且位于同一连通区域的顶点在Reeb图中映射为一个节点.Reeb图能够很好地刻画形状的拓扑结构, 且能起到降维的作用.定义合适的函数f是Reeb图算法的关键, 常用的函数f有高度函数和Morse函数.Shinagawa等人[采用高度函数、权重函数和形状上孔的数量等先验知识自动地生成三维形状的Reeb图.Hilaga等人[通过测地距离、测地线定义了Morse函数, 并基于此提出了多分辨率Reeb算法(MRG), Bespalov等人[在此研究上改进了MRG算法, 并用于CAD模型匹配.Biaso等人[基于Morse函数, 提出了扩展Reeb图算法(extend reeb graph, 简称ERG), 该算法刻画了形状上临界点之间的拓扑关系, 但该算法对形状发生拓扑变化时鲁棒性较差.Tierny J等人[基于特征点的思想构造Reeb图, 其通过特征提取算法提取形状的特征点, 并通过图构造方法生成Reeb图, 并应用Reeb图进行部分形状检索.骨架线, 也被称为三维形状的中轴, 是刻画三维形状拓扑结构的另一个重要方法, 不但能用线段很好地描述模型的结构信息, 而且能高效地保存形状, 提高形状空间存储率和形状检索率.Sundar等人[使用拓扑细化算法提取了形状的骨架线.Cao等人[提出了一种基于拉普拉斯压缩的骨架线提取算法, 该算法可快速提取点云模型的骨架线.Sfikas等人[基于形状的拓扑信息和共形几何特征, 提出了一种非刚性三维形状检索方法, 该算法具有稳健又高效的检索精度和计算速度.
以上3类形状描述符大多应用于描述刚性形状, 对于形状发生等距、拓扑等非刚性变化不鲁棒, 因此不适用于非刚性三维形状匹配.近年来, 应用基于谱分析的形状描述符进行非刚性三维形状匹配成为了一个新的研究热点, 部分研究工作[.谱分析源于形状的内蕴属性, 该方法提供了一种自然的方式进行非刚性三维形状匹配.
谱分析包括谱形状描述符及诱导出的谱距离, 常用的谱形状描述符包括形状DNA(shapeDNA)[、全局点签名(global point signature, 简称GPS)[、热核签名(heat kernel signature, 简称HKS)[、双调合签名(biharmonic signature, 简称BS)[、波动核签名(wave kernel signature, 简称WKS)[等.在一个形状表面上, 由谱形状描述符诱导出的谱距离[是一种较好的度量结构, 具有等距不变性以及对拓扑变化的鲁棒性.常用的谱距离包括交换时间距离(commute-time distance, 简称CD)[、热扩散距离(heat diffusion distance, 简称HDD)[、双调和距离(biharmonic distance, 简称BD)[及波核距离(wave kernel distance, 简称WKD)[.使用谱形状描述符进行三维非刚性形状匹配时, 需要选择数量一致的采样点, 为了避免非刚性形状匹配时采样点的选择问题, 基于SD方法, Bronstein等人提出使用谱距离分布函数作为一种新的形状描述符[.因此, 基于现有研究方法, 本文对基于谱分析的谱形状描述符和谱距离分布函数用于三维非刚性形状匹配进行了详细的研究.
本文第1节给出基于谱分析的三维非刚性形状匹配的一般框架、LB算子的详细介绍及离散化计算.第2节首先详细介绍了几种谱形状描述符:shapeDNA, GPS, HKS, BS, WKS, 给出了谱形状描述符的推导过程及其在离散网格上的计算方法; 其次, 总结与分析了这几种形状描述符在非刚性三维形状匹配中的表现和特性.第3节给出谱距离的定义和形式化表达, 同时给出不同谱距离在三角网格上的离散计算方法以及谱距离分布函数的计算方式.第4节是实验验证部分, 实验中使用不同谱形状描述符和谱距离分布函数进行非刚性三维形状匹配, 观察不同谱形状描述符参数变化对匹配效果的影响, 同时验证了第2节提出的预测的有效性, 并做出合理分析.
现有的形状描述符研究工作
表 1(Table 1)
Table 1 Several studies about summary and analysis of spectral analysis
表 1 谱分析的主要文章综述与分析
年份
第一作者
期刊/会议
题目
简介
2011
Bronstein MM
IEEE Trans. on Pattern Analysis & Machine Intelligence
Shape recognition with spectral distances[
介绍了应用谱距离分布进行非刚性形状识别的方法, 实验比较了HDD以及CD距离分布用于形状识别的性能
2011
Bronstein AM
Computer Science
Spectral descriptors for deformable shapes[
对比了HKS和WKS用于三维形状检索的性能, 并优化了HKS和WKS的参数, 在SREC’10上验证了其参数的优越性
2013
Cao W G
Computer Aided Drafting, Design and Manufacturing
Spectral distance distributions for non-rigid objects[
介绍了应用CD、HDD、BD三种谱形状描述符用于三维非刚性形状分类的方法, 并进行实验比较
2013
R Litman
IEEE Trans. on Pattern Analysis & Machine Intelligence
Learning spectral descriptors for deformable shape correspondence[
基于HKS和WKS构造了一种基于学习的谱形状描述符, 用于形状对应
2014
Patané G.
Pattern Recognition Letters
Laplacian spectral distances and kernels on 3D shapes ☆[
给出谱形状描述符和谱距离形式化表示以及离散化计算方法
2014
Li, Chunyuan,
Multimedia Systems
Spatially aggregating spectral descriptors for non-rigid 3D shape retrieval: A comparative survey[
应用HKS, SIHKS, HMS和WKS进行非刚性三维模型检索
2016
Biasotti S
Computer Graphics Forum
Recent trends, applications, and perspectives in 3D shape similarity assessment[
详细介绍了HKS、SIHKS用于三维形状相似度计算的过程
2016
Patané G.
Computer Graphics Forum
Accurate and Efficient Computation of Laplacian Spectral Distances and Kernels[
详细介绍了的计算过程和性能分析, 分析了谱形状描述符和谱距离的理论意义
2017
Patané G.
ACM SIGGRAPH
An introduction to laplacian spectral distances and kernels: Theory, computation, and applications[
详细介绍了谱形状描述符和谱距离的理论基础、计算过程和应用场景, 从鲁棒性、逼近精度和计算成本等方面讨论了国内外关于谱分析的研究工作
2018
李海生
软件学报
非刚性三维模型检索特征提取技术研究[
对于非刚性三维模型检索特征提取技术进行了详细的研究, 其在广泛调研大量文献和最新成果的基础上对shapeDNA, GPS, HKS, WKS用于三维非刚性形状检索进行了介绍
Table 1 Several studies about summary and analysis of spectral analysis
表 1 谱分析的主要文章综述与分析
(1) 提供应用基于谱分析的形状描述符进行三维非刚性形状匹配的框架, 并给出该方法的原理分析和数值计算;
(2) 系统地对比不同形状描述符的数学定义及算法特性; 从计算精度、鲁棒性、时间复杂度等多方面比较其各自优缺点; 并且在非刚性三维形状标准库中进行了两类描述符的实验比较;
(3) 给出不同谱形状描述符和谱距离分布函数的最优使用场景, 讨论了谱分析应用于非刚性三维形状匹配中存在的问题以及未来的发展趋势, 对谱分析进行推广, 为研究者选择基于谱分析的形状描述符提供参考.
1 基于谱分析的非刚性三维形状匹配框架
本文首先对基于谱分析的非刚性三维形状匹配的框架进行介绍.在数学中, 谱分析是一个广义的方法, 它将一个矩阵的特征向量和特征值理论扩展到一个含有更广泛运算符结构的谱空间中.在形状匹配中, 谱分析是指将形状上的LB算子离散化表示为LB矩阵, 对LB矩阵进行谱分解得到LB算子的特征向量和特征值.利用LB算子的特征值和特征向量, 可以定义出不同的谱形状描述符及其诱导出的不同的谱距离.通过计算一对形状上的谱形状描述符离散值或谱距离分布函数值, 研究者可以对比一对形状的局部或整体对应关系, 得到一对形状的非刚性匹配结果.本节首先给出非刚性匹配谱分析的一般框架, 其次给出LB算子的定义及离散化计算及谱分解形式.
1.1 非刚性匹配谱分析框架
LB算子的特征值与特征向量常常被用来描述模型的形状特性.利用谱形状描述符和谱距离可以很好地进行非刚性形状匹配, 本文给出基于谱分析的非刚性三维形状匹配的一般框架如
图 3
Fig. 3
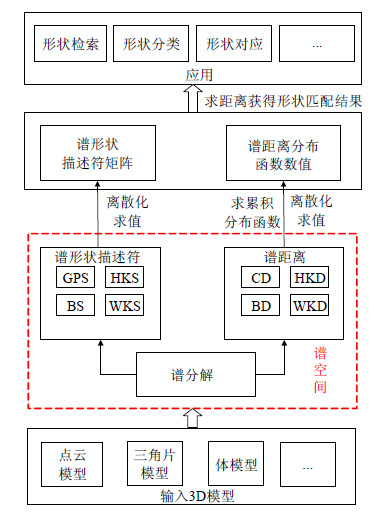
Fig. 3 Non-rigid shape matching framework using spectral analysis
图 3 非刚性形状匹配谱分析框架
● 第1步:输入一对3D非刚性形状(点云模型、三角片模型等).
● 第2步:计算形状上每个采样点的LB算子值, 并将其进行谱分解, 由LB算子特征值和特征向量定义不同的形状描述符, 谱形状描述符可以诱导出谱距离.
● 第3步:对谱形状描述符和谱距离分布函数进行离散化求值, 得到谱形状描述符矩阵和谱距离分布函数矩阵.
● 第4步:应用方差或其他度量方法计算一对形状间谱形状描述符或谱距离分布函数数值, 并选择合适的度量函数进行形状匹配, 形状匹配结果可以应用于形状检索、形状分类、形状对应等.
整个匹配过程中, 形状描述符的选择是重要步骤, 通过选择合适的形状描述符, 研究者就可找到一对形状间的局部或整体匹配关系.
1.2 拉普拉斯-贝尔塔拉米算子
作为谱分析中的重要算子, 拉普拉斯-贝尔塔拉米算子是Laplace算子黎曼流形上的推广.Laplace算子是欧氏空间中作用于光滑函数f的二阶微分算子, 描述为f的梯度的散度[.任意二阶可微函数的Laplace算子定义为
$\Delta f = \nabla \cdot \nabla f = {\nabla ^2}f = \frac{{{\partial ^2}f}}{{\partial {x^2}}} + \frac{{{\partial ^2}f}}{{\partial {y^2}}} + \frac{{{\partial ^2}f}}{{\partial {z^2}}}$
(1)
根据黎曼流形梯度和散度的定义, 若g为流形上的度量张量, G为矩阵{gij}的行列式, 则函数f的LB算子在局部坐标系中定义为[
$\Delta f = \nabla \cdot \nabla f = \frac{1}{{\sqrt G }}\sum\limits_{i,j = 1}^n {{g^{ij}}} \frac{\partial }{{\partial {x^i}}}\left( {\sqrt G {g^{ij}}\frac{{\partial f}}{{\partial {x^j}}}} \right)$
(2)
在非刚性三维形状匹配中, 研究者需要计算离散网格上每个顶点的LB算子值.网格上某顶点vi周围三角形面片示意图如
图 4
Fig. 4
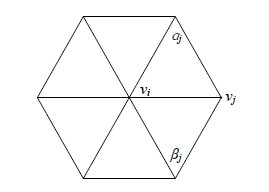
Fig. 4 Diagram of a vertex vi on a triangular mesh
图 4 网格上某顶点vi的三角面片图示
在离散数学中, 有限维离散LB算子通常称为离散LB矩阵, 是对连续LB算子的一种逼近.在顶点数为n的三角网格上定义函数f, 则该函数在网格顶点vi处的离散LB算子可以定义为[
$LB(f({v_i})) = \sum\limits_{j = 1}^n {{\omega _{ij}}(f({v_i}) - f({v_j}))} $
(3)
等式(3)中, 当计算点vi的LB算子时, 考虑网格中的所有顶点.对于网格上某顶点vi, 若仅对其周围三角形面片能量求和, 然后计算其偏导数并合并同类项, 得到该点对应离散LB算子的值:
$LB(f({v_i})) = \frac{\partial }{{\partial f({v_i})}}\sum\limits_{{v_j} \in Neigh({v_i})} {{E_D}({f_{jth{\rm{ - }}tri}})} = \frac{1}{2}\sum\limits_{vj \in Neigh({v_i})} {(\cot {\alpha _j} + \cot {\beta _j})} \cdot |f({v_i}) - f({v_j})|$
(4)
其中, αj和βj分别表示连接vi和vj的边eij两侧的对角, Neigh(vi)表示与顶点vi相邻的顶点的集合.在完备有界的紧致流形上定义的LB算子, 具有对称性和非负性.若将LB算子进行谱分解(或称特征分解)为特征值和特征向量的矩阵乘积形式, 可得到流形上的LB谱, 即LB算子的特征值和特征向量表达式:
$
{\mathit{Δ}_M}{\varphi _i} = {\lambda _i}{\varphi _i}
$
(5)
λ0≥λ1≥…≥λn是LB算子的非负特征值序列, λi是第i个特征值, φi是第i个特征值对应的特征向量.如果在封闭区域使用Neumann边界条件[, 第1个特征值为0, 一般将最小的非零特征值定义为λ1.由于LB算子是半正定算子, 所以λn≥0.LB算子可以解析地计算一些形状几何量(例如矩形、圆柱、圆盘或球面等).如果一些形状, 例如动物、植物等, 变换其形体姿态, 例如在其关节处只有轻微的拉伸, 这种情况被称为近似等距变化, LB算子同样对近似等距变化鲁棒.
2 谱形状描述符
由LB算子的特征值和特征向量以定义不同的谱形状描述符, 例如上文提到的shapeDNA, GPS, HKS, BS和WKS, 本节对几种谱形状描述符的详细定义以及离散计算方法进行介绍.
2.1 ShapeDNA
ShapeDNA是Reuter等人在2005年通过提取黎曼流形表面的LB算子的特征值序列进行非刚性形状检索, 它的主要优点是易于表示形状, 计算简单M上某点x的shapeDNAx可被计算为
$
ShapeDN{A_x}\left( {M,g} \right) = \{ {\lambda _0} \le {\lambda _1} \le {\lambda _2} \le \ldots \le {\lambda _n}\} \in {R_n} \ge 0
$
(6)
g是被定义在形状M上的度量, n为特征值序列的编号, shapeDNA为非负值.ShapeDNA很好地描述了形状的内蕴属性, 不依赖形状的参数化表示.形状上, 所有采样点的shapeDNA组成了shapeDNA矩阵, 确定n的取值后, 可以唯一确定该形状的shapeDNA矩阵, 但相似形状的shapeDNA矩阵非常近似, 因此, 其对于相似形状的区分度较差.
2.2 全局点签名算子
由于同类相似形状的shapeDNA值很近似, 为了提高shapeDNA对同类形状的区分度, Rustamov等人在其基础上定义了一种新的谱形状描述符——全局点签名.如果将形状内在的对称性转化为特征空间, 将非刚性形状的特征空间映射到一个无限维空间——全局点嵌入域(global point signature embedding dominant), 那么在该无限维空间中, 可以定义M上的每点x的GPS(x)可定义为
$GPS(x) = \left( {\frac{{{\varphi _1}(x)}}{{\sqrt {{\lambda _1}} }},\frac{{{\varphi _2}(x)}}{{\sqrt {{\lambda _2}} }},...,\frac{{{\varphi _n}(x)}}{{\sqrt {{\lambda _n}} }}} \right)$
(7)
和shapeDNAx一样, GPS(x)描述形状的全局特征.形状上每个点的GPS(x)都表示一个向量, 一个形状上所有采样点的GPSM表示为一个m×n的矩阵, 其中, m为形状上采样点的数量, n为LB算子特征值数量, 如等式(8)所示.
$GP{S_M} = \left[ {\begin{array}{*{20}{c}}
{\frac{{{\varphi _1}(1)}}{{\sqrt {{\lambda _1}} }},\frac{{{\varphi _2}(1)}}{{\sqrt {{\lambda _2}} }},...,\frac{{{\varphi _n}(1)}}{{\sqrt {{\lambda _n}} }}} \\
{\frac{{{\varphi _1}(2)}}{{\sqrt {{\lambda _1}} }},\frac{{{\varphi _2}(2)}}{{\sqrt {{\lambda _2}} }},...,\frac{{{\varphi _n}(2)}}{{\sqrt {{\lambda _n}} }}} \\
{...} \\
{\frac{{{\varphi _1}(m)}}{{\sqrt {{\lambda _1}} }},\frac{{{\varphi _2}(m)}}{{\sqrt {{\lambda _2}} }},...,\frac{{{\varphi _n}(m)}}{{\sqrt {{\lambda _n}} }}}
\end{array}} \right]$
(8)
由上述定义可知, 一个形状的GPS矩阵维数很高.研究者需要根据应用选择合适的特征值数量n, 以避免较高的计算量.
2.3 热核签名算子
根据热扩散理论, 假定在形状上每点有初始热源μ0(x), 并随时间t在形状M表面上进行热量扩散.在一定时刻, 形状表面上达到热平衡状态.在这个过程中, 定义热核ht(x, y)为t时刻从x点到y点转移所需的热量, 表示热量从一个点传递到另一个点的可能性.等式(9)为形状上的热扩散偏微分方程, 描述了形状表面上温度随时间变化状态.
$\left\{ {\begin{array}{*{20}{l}}
{\left( {\Delta - \frac{\partial }{{\partial t}}} \right)\mu (x,t) = 0} \\
{\mu (x,0) = {\mu _0}(x)}
\end{array}} \right.$
(9)
其中, μ(x, t)是形状M上时间t对应的热量分布函数, Δ是LB算子.该方程的解为
$\mu (x,t) = \int {{h_t}(x,y){\mu _0}(y){\rm{d}}y} $
(10)
同样, 对热核进行谱分解:
${h_t}(x,y) = \sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}{\varphi _i}(x){\varphi _i}(y)} $
(11)
热核能完全表征一个形状表面的几何信息, 如果将热核限制在时间域内, 可得到一个简洁的形状描述符——热核签名:
${h_t}(x,x) = \sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}{\varphi _i}{{(x)}^2}} $
(12)
HKS具有多尺度特性, 能通过调节时间t改变其描述的是形状的局部特征或者全局特征.形状M在不同时间尺度下HKS值分布可表示为
$HK{S_M} = \left[ {\begin{array}{*{20}{c}}
{\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}{t_0}}}{\varphi _i}{{(1)}^2}} ,\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}{t_1}}}{\varphi _i}{{(1)}^2}} ,...,\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}{\varphi _i}{{(1)}^2}} } \\
{\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}{t_0}}}{\varphi _i}{{(2)}^2}} ,\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}{t_1}}}{\varphi _i}{{(2)}^2}} ,...,\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}{\varphi _i}{{(2)}^2}} } \\
{...} \\
{\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}{t_1}}}{\varphi _i}{{(m)}^2}} ,\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}{t_2}}}{\varphi _i}{{(m)}^2}} ,...,\sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t}}{\varphi _i}{{(m)}^2}} }
\end{array}} \right]$
(13)
其中, 每一列代表形状在不同时间t下的HKS值分布.t时刻下, 3个形状的热核签名示意图.可以从图中看出, 当t很小时, 热核签名描述了形状的局部特征[.
图 5
Fig. 5

Fig. 5 Diagram of heat kernel function for a small fixed t on the hand, Homer, and trim-star
图 5 较小t值下手掌、人偶及五角星的热核签名图示
基于HKS, Bronstein等人对HKS进行改进, 提出了具有比例不变性热核签名(scale-invariant heat kernel signature, 简称SIHKS)[.该描述符采用对数采样以及傅里叶变换, 消除了一对形状缩放前后的缩放倍数, 在原有的HKS上增加了缩放比例不变的特性.其具体过程如下.
● 首先, 设缩放系数为β, 对于形状M, 其发生缩放后的形状为M'=βM.参照HKS定义, 缩放后的特征值和特征向量满足λ'=β2λ, φ'=βφ, 则缩放后, 形状M'上某点x处HKS(x)的谱分解形式可写为
${h'_t}(x,x) = \sum\limits_{i = 0}^\infty {{{\rm{e}}^{ - {\lambda _i}t{\beta ^2}}}{\varphi _i}{{(x)}^2}{\beta ^2}} $
(14)
● 其次, 在比例变换下, ${h'_t}(x,x) = {\beta ^2}{h_t}(x,x)$, 对时域上的热核函数进行对数采样, 设时间t=ατ, 得到新的函数方程为hτ(x, x)=h(x, ατ).此时, 比例缩放变换导致的β2的影响转化为时间平移${h'_\tau } = {\beta ^2}{h_{\tau + s}}$, 其中,
$
s = \alpha {\rm{lo}}{{\rm{g}}_\alpha }\beta ;
$
● 最后, 对h取对数, 消除β2的影响:${\dot h_\tau } = {\dot h_{\tau + s}}$, 则${\dot h_\tau } = \log {h_{\tau + 1}} - \log {h_\tau }$.接着对${\dot h_\tau }$进行傅里叶变换, 使时域的平移变换转移到复数域:
$
H'(\omega ) = H'(\omega ){e^2}^{{\rm{ \mathsf{ π} }}\omega s}
$
(15)
对等式(15)两边取傅里叶模后得到等式(16):
$
\left| {H'(\omega )} \right| = \left| {H\left( \omega \right)} \right|
$
(16)
文献[
图 6
Fig. 6

Fig. 6 Scale-invariant heat kernel signature for the initial and scaled shape
图 6 原始形状和缩放变化后形状的缩放不变热核签名图示
2.4 双调和算子
为了同时兼顾形状的局部特性和全局特性, 在HKS和GPS的基础上, 将LB算子的特征值和特征向量进行另一种组合, 在形状M上的某点x定义另一种谱形状描述符, 即双调和签名:
$BS(x) = \left( {\frac{{{\varphi _1}(x)}}{{{\lambda _1}}},\frac{{{\varphi _2}(x)}}{{{\lambda _2}}},...,\frac{{{\varphi _n}(x)}}{{{\lambda _n}}}} \right)$
(17)
与GPS类似, 形状上的每个点的BS(x)都表示一个n维向量.一个形状的BSM表示为一个m×n的矩阵, 其中, m为形状上点的数量, n为LB算子谱分解数量.
$B{S_M} = \left[ {\begin{array}{*{20}{c}}
{\frac{{{\varphi _1}(1)}}{{{\lambda _1}}},\frac{{{\varphi _2}(1)}}{{{\lambda _2}}},...,\frac{{{\varphi _n}(1)}}{{{\lambda _n}}}} \\
{\frac{{{\varphi _1}(2)}}{{{\lambda _1}}},\frac{{{\varphi _2}(2)}}{{{\lambda _2}}},...,\frac{{{\varphi _n}(2)}}{{{\lambda _n}}}} \\
{...} \\
{\frac{{{\varphi _1}(m)}}{{{\lambda _1}}},\frac{{{\varphi _2}(m)}}{{{\lambda _2}}},...,\frac{{{\varphi _n}(m)}}{{{\lambda _n}}}}
\end{array}} \right]$
(18)
BS通过正则化拉普拉斯算子的特征值, 很好地平衡了形状的局部特征和全局特征.BS算子来源于双调和微分方程, 该算子在形式上与GPS非常相像, 但是性能却有很大提升, 分母由LB算子的特征值的平方根变为LB算子的特征值, 大大加快了描述符的归一化.与GPS一样, 当我们选用BS表示形状时, 需要根据应用场景选择合适的谱分解数量n, 以避免较高的计算量.
2.5 波核签名
对于形状上的每个点, 通过测量不同能量级的量子粒子的平均概率分布, 文献[
$\left\{ {\begin{array}{*{20}{l}}
{\frac{{\partial \phi }}{{\partial t}}(x,t) = i\Delta \phi (x,t)} \\
{\phi (x,0) = {\phi _0}x}
\end{array}} \right.$
(19)
波函数的形式表达类似于热核函数, 但意义却截然不同:热核函数表示是热量耗散, 波动函数表示了能量的振荡.其中, x是形状上任意一点, Δ是LB算子, i是虚数, LB算子和i的乘积确保能量经过不同频率振荡后不会衰减.通过及谱分解理论可得, 波函数ϕ(x, t)的谱分解形式为
$\phi (x,t) = \sum\limits_{k = 0}^\infty {{f_k}(t){\varphi _k}(x)} $
(20)
其中, fk(t)为t时刻粒子的第k个频率, φk(x)为第k个频率对应的特征向量, 可计算如下:
${f_k}(t) = \int\limits_X {{{\bar \phi }_{k(x)}}\phi (x,t)dx} $
(21)
当t=0时, 表示期望值为E, 频率λk的概率分布.Laplace谱没有重复值, 结合公式(20)及公式(21)可得:
$\phi (x,t) = \sum\limits_{k = 0}^\infty {{f_k}(0){{\rm{e}}^{i{\lambda _k}t}}{\varphi _k}(x)} $
(22)
|ϕ(x, t)|2为点x处粒子的概率分布.由于时间参数t对概率分布没有直接影响, 若只考虑能量参数, 将WKS算子定义为点x处能量为E的一个粒子可被测量到平均概率:
$WKS(E,x) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_0^T {|\phi (x,t){|^2}} $
(23)
由于${{\rm{e}}^{ - i{E_k}t}}$与L2范数正交, 若将能量概率分布代替频率概率分布——fk(0)=fE(λk), 则联合公式(22)、公式(23), WKS可写为
$WKS(E,x) = \sum\limits_{k = 0}^\infty {|{f_E}({\lambda _k}){|^2}|{\varphi _k}(x){|^2}} $
(24)
由上述可知, WKS采用带通滤波器, 因此可以很好地分离形状, 如
图 7
Fig. 7
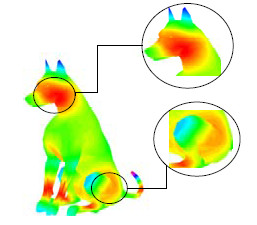
Fig. 7 Wave kernel signature on a dog
图 7 狗的波动核签名图示
公式(24)中, WKS的表达式具有一般性, 可以通过选择不同能量概率分布函数fE(λk)得到不同的WKS.选择对数正态分布函数作为能量概率分布函数, 则WKS可写为
$\left\{ {\begin{array}{*{20}{l}}
{WKS(x,{e_N}) = {C_e}\sum\limits_k {\varphi _k^2(x){{\rm{e}}^{\frac{{ - {{({e_N} - \log {\lambda _k})}^2}}}{{2{\sigma ^2}}}}}} } \\
{{C_e} = {{\left( {\sum\limits_k {{{\rm{e}}^{\frac{{ - {{({e_N} - \log {\lambda _k})}^2}}}{{2{\sigma ^2}}}}}} } \right)}^{ - 1}}}
\end{array}} \right.$
(25)
eN为能量规模参数, eN=log(E), λk为LB算子第k个特征向量, σ为正态分布的方差, Ce为正则化WKS函数.在实验中, 本文采用与文献[
$WK{S_M} = \left[ {\begin{array}{*{20}{c}}
{WK{S_1}({e_1}),WK{S_1}({e_2}),...,WK{S_1}({e_N})} \\
{WK{S_2}({e_1}),WK{S_2}({e_2}),...,WK{S_2}({e_N})} \\
{...} \\
{WK{S_m}({e_1}),WK{S_m}({e_2}),...,WK{S_m}({e_N})}
\end{array}} \right]$
(26)
其中, WKSM(eN)形状第m个顶点在能量规模为N下的WKS值, 每列代表不同能量规模下形状M每点的WKS值.当我们选用WKS表示形状时, 需要根据应用选择合适的能量规模eN, 以突出WKS的优势.
2.6 谱形状描述符比较
在谱形状描述符中, shapeDNA的研究时间最早, 因此整体性性能相对较差, 但其为之后谱形状描述符的发展奠定了基础.每点的shapeDNA由LB算子的前n个特征值确定, 忽略了LB算子的特征向量的作用, shapeDNA最大的优点是易于理解, 计算简单.但对局部特征的描述能力较弱, 不适合相似形状的快速区分.
GPS由LB算子的前n个特征向量比上特征值得到.从定义上看, GPS更加注重低频相关的信息, 但对于形状发生非刚性形变(变化较小)时, 形状上一点的GPS值也会完全改变, 增加额外的算法复杂度, 性能并不好.总体来说, GPS能够很好地反映形状上所有采样点的上下文信息, 但对局部特征的描述能力较弱, 适合非刚性形状的粗糙匹配, 不适用于局部匹配.
HKS定义了点x处的局部和全局属性.由于形状上的热扩散本质近似布朗运动, 因此有较强的鲁棒性以弱化局部噪声的影响.作为低通滤波器的集合, HKS主要由低频传输, 能够很好地描述形状的局部几何信息.当时间t比较短时, 形状上每个点的HKS值与该点的高斯曲率直接相关, 具有很强的信息存储性.但HKS过于强调低频信息, 会过滤掉一些高频率信息, 损害精确定位特征的能力.因此相比较其他3种算子, HKS表征形状时不能很好地分离不同频率区域.此外, 由于HKS对时间参数敏感, 所以在某个时刻下, 不能同时表征形状的局部属性和全局属性.SIHKS拥有HKS所有的优点, 还具有缩放不变性, 但是其理解相对较难且计算复杂.
BS平衡了大尺度距离(反映全局特性)和小尺度距离(反映局部特性), 具有多尺度特性.它不依赖于时间参数, 克服了HKS依赖时间参数重的缺点, 同时克服了GPS没有多尺度特性的缺点.然而, 由于BS具有调和性质, 单独表征形状的局部及全局属性性能较差.
WKS同样对时间参数自由, 其最大优点是采用带通滤波器能清楚地分离形状上的不同频率集合, 且允许访问高频率信息, 从而增加算子的精确匹配能力.此外, WKS通过选择不同的能量规模而具有多尺度特性, 若选择能量级别较高的量子粒子, 波长越短, 其分布越靠近形状上的点, 此时反映形状的局部特性; 反之, 能量级别较低的量子粒子反映形状的全局特性.所以在匹配时, 研究者应该根据应用场景选择一个合适的能量规模.
几种谱形状描述符在不同变换下鲁棒性等级见
表 2(Table 2)

Table 2 Robustness levels of several spectral shape descriptors under different transformations
表 2 几种谱形状描述符在不同变换下鲁棒性等级
名称
局部/全局性质
等距变化
缩放不变
下采样
加入洞
噪声
拓扑
ShapeDNA
全局
优
差
优
良
优
优
GPS
全局
优
差
优
优
优
优
HKS
局部/全局
优
差
优
优
优良
优
SIHKS
局部/全局
优
优
优
优
优良
优
BS
局部 & 全局
优
差
优良
优良
优
优良
WKS
局部/全局
优
差
优
优
优良
优
Table 2 Robustness levels of several spectral shape descriptors under different transformations
表 2 几种谱形状描述符在不同变换下鲁棒性等级
3 谱距离分布函数
谱距离(shape spectral distance distribution)源于谱分析, 谱距离由形状表面上定义的谱形状描述符诱导得到, 包括热扩散距离、交换时间距离、双调和距离等.若在形状M上定义度量空间, 则由谱形状描述符诱导出的谱距离可定义为[
${d^2}(x,y) = \sum\limits_{i = 0}^N {{\phi ^2}({\lambda _i})|\phi (x) - \phi (y){|^2}} $
(27)
其中, ϕ(λi)为不同谱形状描述符使用的滤波器.在三角面片上, 谱距离的离散化形式为[
${d^2}(p,q) = \sum\limits_{i = 0}^N {{\phi ^2}({\lambda _i})|{v_{{p_i}}} - {v_{{q_i}}}{|^2}} ,N \to \infty $
(28)
其中, p, q为三角面片上的顶点, ${v_{{p_i}}},{v_{{q_i}}}$分别代表顶点p和q上LB算子第i个特征向量.前文中提到的另一类基于谱分析的形状描述符就是谱距离分布函数, 基于SD方法的研究, Brostein等人通过统计形状上任意两点间的谱距离, 构造了谱距离分布函数最为一种新的形状描述符.假定形状M上任意两点的谱距离为d(x, y), 若δ是距离阈值, μ是定义在M中的范数矩阵, χ是指示函数, 则谱距离频率直方图可以计算为
${p_M}(n\delta ) = \int {{\chi _{(n - 1)\delta < d(x,y) \leqslant n\delta }}{\rm{d}}\mu (x){\rm{d}}\mu (y)} $
(29)
在概率论与统计学中, 概率密度函数(probability density function, 简称PDF)是一个实值随机变量, 用于描述多随机变量的分布, 再由公式(29)可得谱距离分布函数可计算为
${f_M}(n\delta ) = \frac{{\rm{d}}}{{{\rm{d}}\delta }}\int\limits_0^n {{p_M}(n\delta ){\rm{d}}\delta } $
(30)
谱距离分布函数作为一种线性形状描述符, 继承了谱距离的特征, 具有以下特点.
(1) 采样不变性:对于形状M, 如果对M的三角网格模型的顶点进行采样, 包括上采样和下采样, 则采样前后的形状的谱距离分布函数保持不变.
(2) 等距不变性:由于LB算子是形状的内蕴算子, 所以等距形状中任意两点的谱距离具有等距不变形.因此, 等距形变前后, 形状的谱距离分布函数理论上保持不变.但是在下文中, 我们给出了不同谱距离的谱分解计算形式, 在实际应用中, 一般取前100个特征值和特征向量.因此在实际的实验中, 等距形状的谱距离分布函数与原始形状的谱距离分布函数值相似.
(3) 拓扑鲁棒性:相对测地距离分布, 谱距离分布对拓扑变化的敏感性较低, 谱距离分布函数具有较强的拓扑鲁棒性.
(4) 无需预处理:相对于谱形状描述符, 应用谱距离分布进行三维非刚性形状匹配时, 不需要寻找数量相同的采样点, 也不需要配准采样点.
下文就详细对这4种谱距离进行介绍.
3.1 交换时间距离
根据第2.3节, 在GPS域中的内积可定义交换时间距离:
$
G\left( {x,y} \right) = GPS\left( x \right) \cdot GPS\left( y \right)
$
(31)
G(x, y)是两个无限维向量的内积, 交换时间距离可写为
$d_c^2(x,y) = \int\limits_{t = 0}^\infty {{G^2}(x,y){\rm{d}}t} $
(32)
交换时间距离反映了连接一对点之间随机游走的平均时间.通过谱分解, 交换时间距离可以表达为
$d_c^2(x,y) = \sum\limits_{i = 1}^{N \to \infty } {\frac{{{{(\varphi (x) - \varphi (y))}^2}}}{{{\lambda _i}}}} $
(33)
其离散化形式为
$d_c^2(p,q) = \sum\limits_{i = 1}^{N \to \infty } {\frac{{{{({v_{{p_i}}} - {v_{{q_i}}})}^2}}}{{{\lambda _i}}}} $
(34)
热扩散距离和交换时间距离的关系为
$\int_{{\kern 1pt} 0}^{{\kern 1pt} + \infty } {{d_h}(x,y){\rm{d}}t} = {d_c}(x,y)$
(35)
热扩散距离反映了形状表面上两个点在时间t内的路径连通性, 而交换时间距离是一对点之间在平均时间t内随机游走的扩散长度之和.
3.2 热扩散距离
热扩散距离由扩散核导出, 并应用于降维和数据参数化等问题.扩散距离描述了形状M上点x与点y之间在时刻t时的连通率.将形状M上的随机运动看作是布朗运动, 在这种情况下, 扩散距离是对形状M上时间t时两点间的布朗运动的平均, 更直观上的理解为两个热核之间的信息交互.所以形状上的两点x和y之间的扩散距离可以由下面的等式定义
$d_h^2(x,y) = \int_{{\kern 1pt} s} {{{({h_t}(x,z) - {h_t}(y,z))}^2}{\rm{d}}{\mu _z}} $
(36)
根据热核的谱分解形式以及热扩散理论, 热扩散距离(也称热核距离)表示为
$d_h^2(x,y) = \sum\limits_{i = 1}^{N \to \infty } {{e^{ - 2t{\lambda _i}}}{{({\varphi _i}(x) - {\varphi _i}(y))}^2}} $
(37)
为了不失一般性, 特征值从1开始, 离散化形式为
$d_d^2(p,q) = \sum\limits_{i = 1}^{N \to \infty } {{e^{ - 2t{\lambda _i}}}{{({v_{{p_i}}} - {v_{{q_i}}})}^2}} $
(38)
热扩散距离反映了扩散时间t内两点间的热流连通性.由于该距离是定义在形状表面的距离, 所以是一个内蕴距离, 当扩散时间t的取值很小时, 此时热量扩散范围较小, 该距离只能描述形状的局部特性; 当t的取值较大时, 该距离可以描述形状的全局属性, 最后热量扩散直至达到热平衡状态.但t取值并不是越大越好, 合适的t取值[为1/λj, λj为第LB算子的第1个非零特征值.
3.3 双调和距离
类似GPS映射, 双调和映射定义了一个无限维的双调和空间.
双调和域中的内积可定义双调和距离[:
$
B\left( {x,y} \right) = BS\left( x \right) \cdot BS\left( y \right)
$
(39)
B(x, y)是两个无限维向量的内积, 双调和距离可表示为
$d_b^2(x,y) = \int\limits_{t = 0}^\infty {{B^2}(x,y){\rm{d}}t} $
(40)
通过谱分解, 双调和距离可写为
$d_b^2(x,y) = \sum\limits_{i = 1}^{N \to \infty } {\frac{{{{(\varphi (x) - \varphi (y))}^2}}}{{\lambda _i^2}}} $
(41)
离散形式可写为
$d_b^2(p,q) = \sum\limits_{i = 1}^{N \to \infty } {\frac{{{{({v_{{p_i}}} - {v_{{q_i}}})}^2}}}{{\lambda _i^2}}} $
(42)
3.4 波核距离
文献[2范式定义波核距离, 类似于热核距离, 波核距离的谱分解形式为
$d_w^2(x,y) = {C_e}\sum\limits_{i = 1}^{N \to \infty } {{{\rm{e}}^{^{\frac{{ - {{(e - \log {\lambda _i})}^2}}}{{2{\sigma ^2}}}}}}{{(\varphi (y) - \varphi (x))}^2}} $
(43)
离散化形式为
$d_w^2(p,q) = {C_e}\sum\limits_{i = 1}^{N \to \infty } {{{\rm{e}}^{\frac{{ - {{(e - \log {\lambda _i})}^2}}}{{2{\sigma ^2}}}}}{{({v_{{p_i}}} - {v_{{q_i}}})}^2}} $
(44)
4 实验与分析
为了对几种谱形状描述符和谱距离分布函数进行对比, 本文在64位32G内存, win10系统的Matlab2015上进行了实验上进行了实验(注:由于shapeDNA最早被研究, 性能较差, 因此在本文不加入比较).评估这种方法所使用的是TOSCA 2010(tools for surface comparison and analysis)数据集(高分辨率, http://tosca.cs.technion.ac.il/data/toscahires-mat.zip)[、SHREC 2011数据集(鲁棒性, http://tosca.cs.technion.ac.il/book/shrec_robustness2010.html)[和SHREC 2015数据集(标准型, http://www.cs.cf.ac.uk/shaperetrieval/shrec15/SHREC15.zip). TOSCA 2010数据集为非刚性形变的形状匹配提供了大量高清三维形状,
图 8
Fig. 8

Fig. 8 Part of the shapes of TOSCA 2010 database
图 8 TOSCA 2010数据库中的部分形状
图 9
Fig. 9
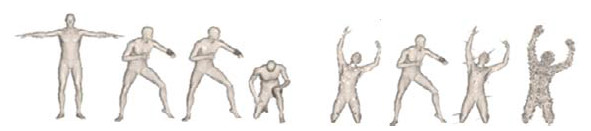
Fig. 9 Part of the shapes of SHREC 2011 database
图 9 SHREC 2011数据库中的部分形状
SHREC 2015数据库由SHREC 2011[和SHREC 2014[中的部分形状组合而成, 包含10类形状, 每类形状包含了基础形状的等距变化、近似等距变化、拓扑变化及加洞等非刚性变化, 共计100个形状, 为非刚性三维形状检索提供标准形式,
图 10
Fig. 10

Fig. 10 Part of the shapes of SHREC 2015 database
图 10 SHREC 2015数据库中的部分形状
4.1 谱形状描述符参数比较
HKS具有多尺度特性, 由时间参数t决定该点描述的是形状的的局部或全局属性.t=0.5时, 此时热量刚开始扩散, 只能描述行david足部的局部几何信息, 此时, HKS值与足部的高斯曲率值直接相关; 当t=1时, 热量扩散到形状的大部分区域; 当t=3.0时, 热量扩散到形状整个表面, 此时, HKS描述形状的全局几何信息.
图 11
Fig. 11
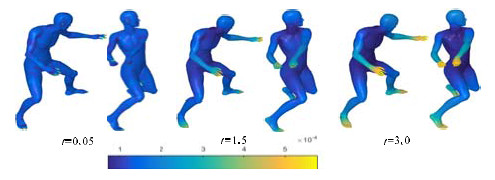
Fig. 11 Non-rigid shape matching using heat kernel signature under different time t (shape: david 1 & david 10)
图 11 在不同时间t下应用热核签名进行一组非刚性形状匹配(shape: david 1 & david 10)
WKS对时间参数自由, e100作为合适的能量规模.
图 12
Fig. 12
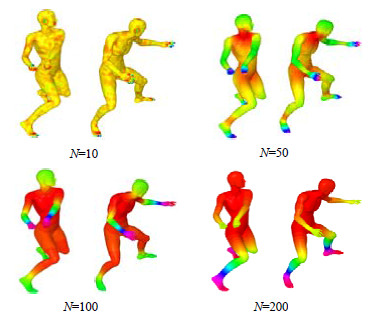
Fig. 12 Non-rigid shape matching using wave kernel signature under different energy scale eN(shape: david 1 & david 10)
图 12 在不同能量级(eN)下应用波动核签名进行一组非刚性形状对应(shape: david 1 & david 10)
图 13
Fig. 13

Fig. 13 Compared with GPS, HKS, BS, WKS robustness in isometric, sampling, cave, noise and topological changes (t=3.0, λNum=100, e100)
图 13 对比GPS、HKS、BS、WKS在等距、采样、加洞、噪声及拓扑变化下鲁棒性(t=3.0, λNum=100, e100)
4.2 谱形状描述符用于三维非刚性形状匹配比较
从
图 14
Fig. 14
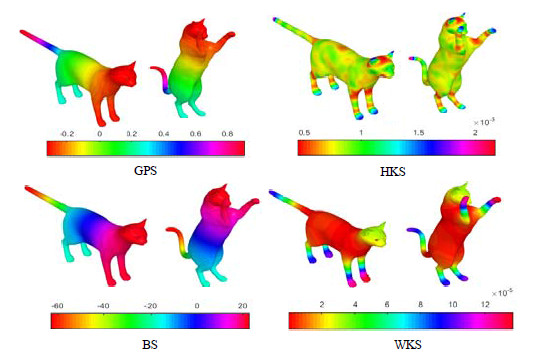
Fig. 14 Non-rigid shape matching using GPS, HKS, BS, WKS (shape: cat 0 & cat 1, t=3.0, λNum=100, e100)
图 14 应用GPS、HKS、BS、WKS进行非刚性形状匹配(shape: cat 0 & cat 1, t=3.0, λNum=100, e100)
而当时间参数足够大时, HKS能表征cat 0与cat 1的局部几何信息和全局几何信息, 但由于HKS使用的都是一些低通滤波器, 形状的高频率信息被抑制, 不能精确地表示形状, 相比GPS, HKS能分清cat的腿部和身体, 但没有办法区分猫的前足和后足; BS表现最佳, cat 1相对cat 0尾巴发生较大扭曲, 此时, cat 0和cat 1为近似等距变化, BS能够明确地描述尾部的近似等距变化且匹配度高; 同时, WKS在猫的尾部匹配度同样较高, 且相比HKS, WKS使用带通滤波器, 减少低频的影响, 在图中能够清楚地分离出形状的频带区域, 具有优越的特征定位, 且能区分猫的四足, 适合高精度的匹配, 但算法时间复杂度较高.
通过10次实验求取平均值, 几个形状描述符耗费时间如O(n), n为三维形状上采样点的个数.由于GPS和BS都是高维向量, 因此其耗费时间要多于HKS; 同时, WKS采用带通滤波器分离形状上的不同频率集合, 对于形状的细节刻画较多, 因此时间耗费相对最高.为了比较应用不同谱形状描述符进行非刚性三维形状匹配的匹配度, 实验中, 我们计算一对形状上采样点的谱形状描述符的相关系数R=corr2(A, B)作为三维非刚性形状匹配的匹配度(即一对形状的相似度), 结果如
表 3(Table 3)

Table 3 Time-consuming of non-rigid shape matching using spectral shape descriptors
表 3 应用谱形状描述符进行非刚性形状匹配所耗费时间
时间(s)
形状名称(m:文件大小)
Centuar (m=1722k)
Cat (m=3094k)
Vitoria (m=5106k)
GPS
36.687
65.933
101.482
121.088
HKS
28.201
48.841
83.918
106.241
BS
36.665
64.636
101.269
120.789
WKS
48.893
79.364
123.798
145.116
Table 3 Time-consuming of non-rigid shape matching using spectral shape descriptors
表 3 应用谱形状描述符进行非刚性形状匹配所耗费时间
表 4(Table 4)

Table 4 Non-rigid shape matching using spectral shape descriptors
表 4 应用谱形状描述符进行非刚性形状匹配
Corr2
形状名称(m:文件大小)
Centuar (m=1722k)
Cat (m=3094k)
Vitoria (m=5106k)
David (m=5888k)
GPS
0.863 0
0.864 1
0.861 1
0.855 6
HKS
0.877 0
0.869 1
0.857 4
0.852 4
BS
0.907 5
0.907 8
0.907 9
0.901 5
WKS
0.931 4
0.919 1
0.917 4
0.915 3
Table 4 Non-rigid shape matching using spectral shape descriptors
表 4 应用谱形状描述符进行非刚性形状匹配
4.3 谱距离分布用于三维非刚性形状匹配比较
有效的谱距离分布函数可以区分不同类别的形状, 且对于形状发生非刚性变化, 谱距离概率分布趋势差别较小, 故可以通过匹配形状的谱距离分布, 进行三维非刚性形状匹配[.
图 15
Fig. 15
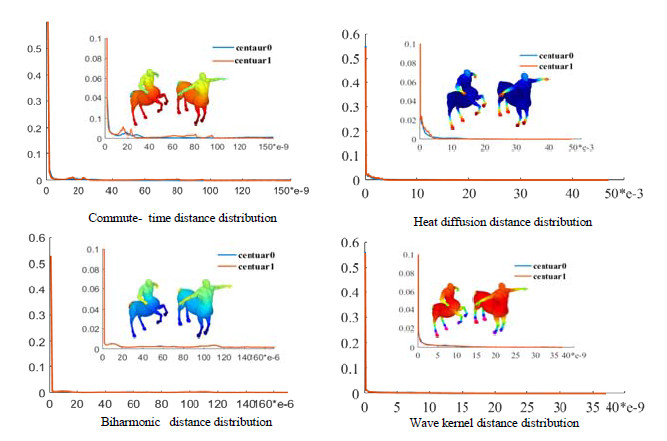
Fig. 15 Distribution function of four spectral distances for non-rigid shapes using matching (shape: centaur 0 & centua 1)
图 15 4种谱距离分布函数进行非刚性形状匹配(shape: centaur 0 & centua 1)
通过10次实验求取平均值, 几个谱距离分布函数的耗费时间见O(n2), n为三维形状上采样点的个数.为了比较非刚性形状应用不同谱形状分布函数进行匹配的匹配度, 实验中, 为了直接得到一对形状的匹配度, 我们同样计算一对形状的谱形状距离分布函数的相关系数作为三维非刚性形状匹配的匹配度(即一对形状的相似度), 结果见
表 5(Table 5)

Table 5 Time-consuming of non-rigid shape matching using thedistribution function of four spectral distances
表 5 应用4种谱距离分布函数进行非刚性形状匹配所耗费时间
时间(s)
形状名称(m:文件大小)
Centuar (m=1722k)
Cat (m=3094k)
Vitoria (m=5106k)
David (m=5888k)
CDD
836.523
3 365.75
4 719.546
5 136.651
HDD
805.749
3 013.22
4 786.671
5 106.334
BD
836.451
3 464.73
4 701.269
5 120.755
WKD
868.342
3 521.323
4 723.656
5 135.446
Table 5 Time-consuming of non-rigid shape matching using thedistribution function of four spectral distances
表 5 应用4种谱距离分布函数进行非刚性形状匹配所耗费时间
表 6(Table 6)

Table 6 Non-rigid shape matching using the distribution function of four spectral distances
表 6 应用4种谱距离分布函数进行非刚性形状匹配
Corr2
形状名称(m:文件大小)
Centuar (m=1722k)
Cat (m=3094k)
Vitoria (m=5106k)
David (m=5888k)
CDD
0.986 3
0.987 6
0.989 5
0.982 4
HDD
0.992 8
0.993 9
0.994 1
0.995 2
BD
0.995 6
0.995 8
0.995 9
0.997 1
WKD
0.997 4
0.997 1
0.997 9
0.998 5
Table 6 Non-rigid shape matching using the distribution function of four spectral distances
表 6 应用4种谱距离分布函数进行非刚性形状匹配
结合
图 16
Fig. 16
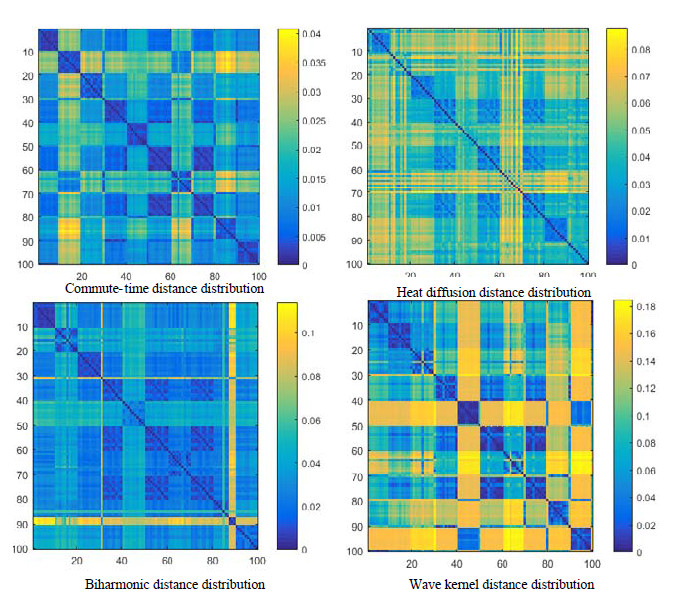
Fig. 16 Thermodynamic diagram of non-rigid 3D shape matching using four spectral distances based on SHREC 2015 database
图 16 基于SHREC 2015数据库, 应用4种谱距离进行非刚性三维形状匹配的热力图
如t; WKD既能描述形状的局部属性, 又能描述形状的全局属性, 同时, 相对于其他3种谱距离分布函数, WKD能够精准地描述不同类的形状, 对于male0, male13和male16的区分度更大.
表 7(Table 7)

Table 7 Precision ratio of 3D Non-rigid shape retrieval using the distribution function offour spectral distances based on SHREC 2015 database
表 7 基于SHREC 2015数据库, 应用4种谱距离分布函数进行非刚性三维形状检索查准率
L2距离
形状名称
Centuar
Ants
Gorilla
Male 0
Female_ thin
Male 13
Dog
Male 16
Plies
Male_body builder
平均查准率
CDD
1.0
1.0
0.9
0.5
1.0
0.4
0.8
0.5
0.9
0.9
0.79
HDD
0.9
0.8
1.0
0.8
0.6
0.6
0.5
0.5
1.0
0.5
0.72
BD
1.0
0.9
1.0
0.5
1.0
0.5
0.6
0.5
1.0
1.0
0.80
WKD
1.0
0.9
0.6
0.9
1.0
0.6
1.0
0.6
1.0
1.0
0.86
Table 7 Precision ratio of 3D Non-rigid shape retrieval using the distribution function offour spectral distances based on SHREC 2015 database
表 7 基于SHREC 2015数据库, 应用4种谱距离分布函数进行非刚性三维形状检索查准率
4.4 问题与展望
通过实验比较了不同谱形状描述符和谱距离分布函数进行非刚性三维形状匹配的性能, 可以发现利用基于谱分析的形状描述符进行非刚性形状匹配效果较好.在4类谱形状描述符中, WKS和WKD整体匹配表现性能最优, 适用于精细匹配, 但时间复杂度较高, 不适用于大规模形状的快速匹配; BS和BD性能次之, 能同时调和地表示形状的局部及全局信息, 但过于强调函数同时描述形状的局部和全局性质, 也会弱化形状的真实全局和局部特性; HKS和HDD对时间参数敏感, 所以仅凭某时刻t下HKS值进行形状的非刚性匹配性能较差, 若能比较形状上每个点或部分特征点的一段时间序列下的HKS值, 则能提高匹配性能, 且HKS适用于部分匹配; GPS和CDD整体匹配度较低, 适用于快速匹配和粗匹配, 但不适用部分匹配.同时, 使用4种谱距离分布函数进行三维非刚性形状匹配时, 无法得到形状部分匹配结果, 只能得到一对形状的全局匹配结果, 其时间复杂度和空间复杂度也比谱形状描述符复杂度高.在未来的研究工作中, 针对不同变化类型的形状(如一些近似等距变化或大变形形状)及不同的应用场景, 应结合几种描述符的优点, 考虑同时使用多个描述符的权重组合或其他改进, 提升非刚性三维形状匹配度.
5 总结
本文给出基于谱分析的形状描述符进行非刚性三维形状匹配的方法流程, 详细介绍了几种谱形状描述符和谱距离分布函数, 并在以下几方面对比了不同形状描述符的性能:(1)局部及全局属性; (2)有无参数及参数选择; (3)时间复杂度; (4)最优匹配度; (5)适用匹配场景; (6)整体表现性能.通过实验, 证明了本文预估的正确性.谱分析是一个易于理解、普适且鲁棒的分析方法, 基于谱分析的形状描述符在非刚性三维形状整体匹配中表现出了优异的性能, 我们希望提升基于谱分析的形状描述符在非刚性形状匹配中重要的理论意义及并推动其在工程应用价值的发展.同时, 在未来的工作中, 我们会对基于谱分析的形状描述符进行非刚性三维形状局部匹配进行进一步研究.
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!