史上最全基础排序算法(动图)
目录
1.冒泡排序
2.选择排序
3.二分查找(前提顺序结构-已序结构)
4.插入排序
5.希尔排序(插入排序的优化)
6.*快速排序
7.基数排序(桶子法)空间复杂度利用最高
8.归并排序(分治法)
1.冒泡排序
原理: 元素之间两两比较,大的往上冒
趟数+次数 =元素数量
实现 :内外循环
外层: 确定核心事件做的次数:趟数
内层:确定每一趟的次数
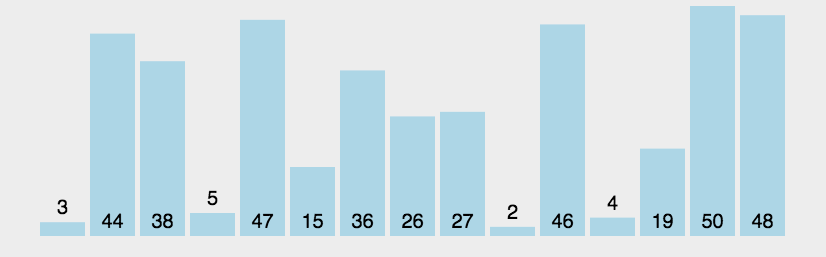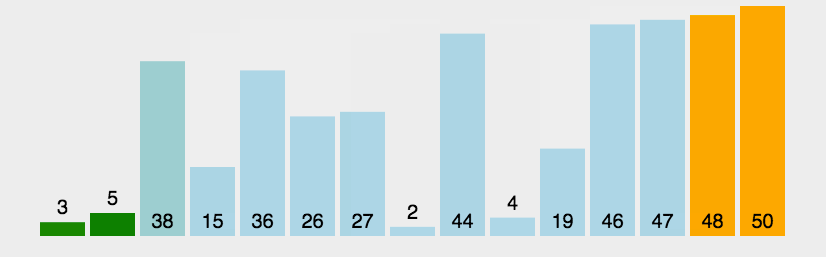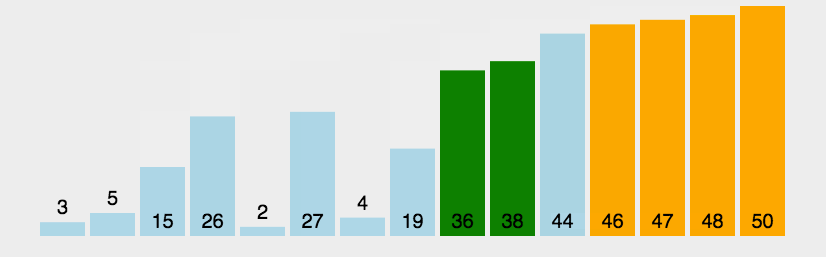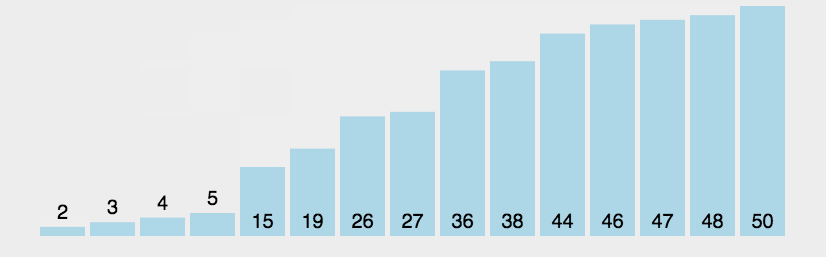
以下是代码
void Bubble_sort (int *arr, int length)
{for(int i =0;iarr[j+1])swap(arr[j],arr[j+1]);}}
}
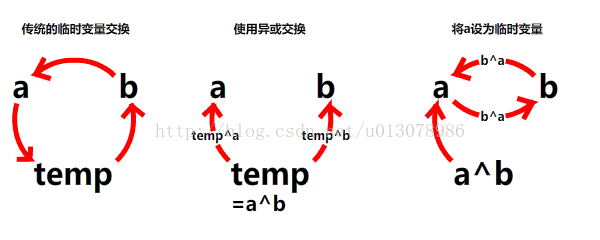
*优化 数据保存在栈将temp ,j 定义在函数外 *异或交换
c^a=b;
c^b=a;
可以很惊奇的发现,将两数异或的结果与其中一数再进行异或,可以得到另一个数。 原理很简单,两数异或的结果保存了两个数上每一个二进制位不同或相同的信息,如果相应的二进制位不同,就标志为1,如果相同,则标志为0。
2.选择排序
原理:每一次从待排序的元素中挑出最小(最大的)放到已序末尾
1.选取一个最小的(最大的)放在待序元素的开头(末尾)
比较趟数 =元素-1
每一趟次数 =趟数 -1

void select_sort(int *arr,int size)
{for(int i =size-1;i>0;i++)//for(int i=0;i3.二分查找(前提顺序结构-已序结构)

原理:mid =left + (right -left)/2
定义左右中游标
每次分一半
int binary_search(int *arr,int size,int findval)
{int mid,left,right;//定义游标left =0;right = size -1;while(left<=right){//1.确定中位数 mid = left +((right+left)>>1);//2.和中位数比较if(arr[mid] ==findval)return mid;//如果不是中位数缩小范围 -升序if(findvalarr[mid])//说明在右侧left =mid +1;}return -1;
} 4.插入排序
原理:每轮插入一个进行比较
每一轮排序完前面都是有序的
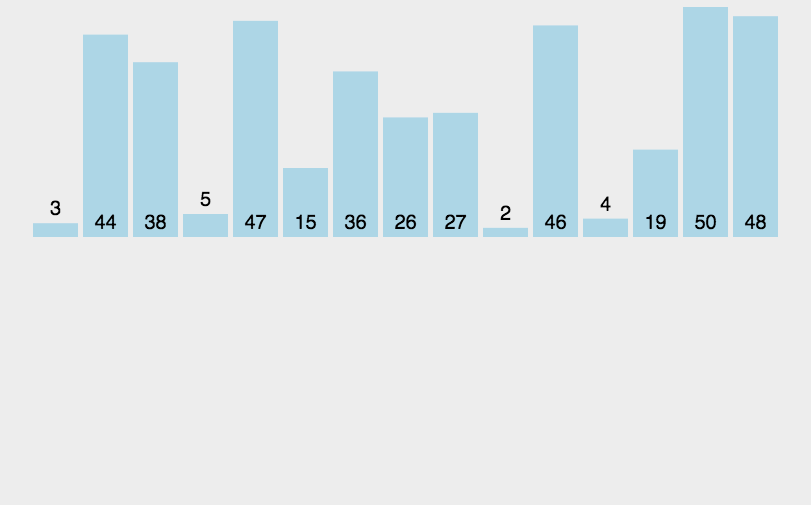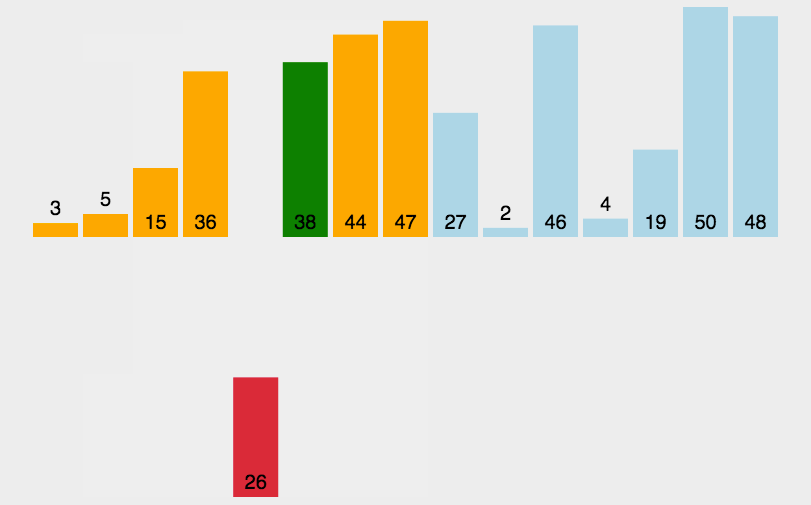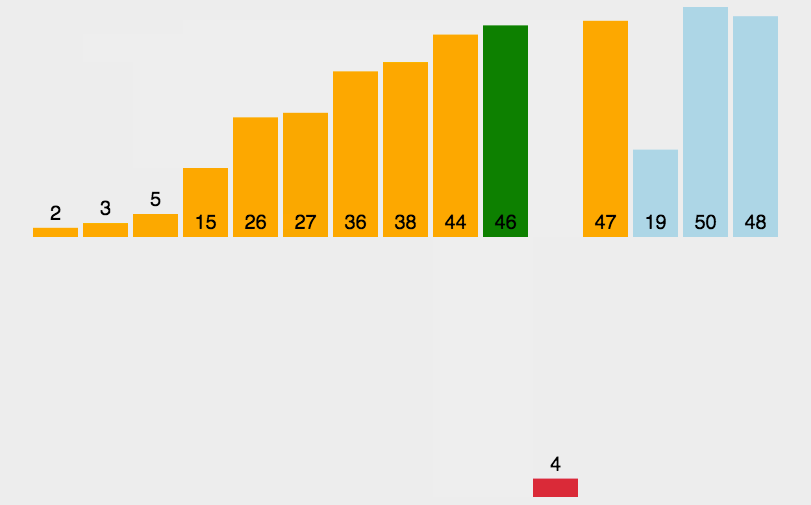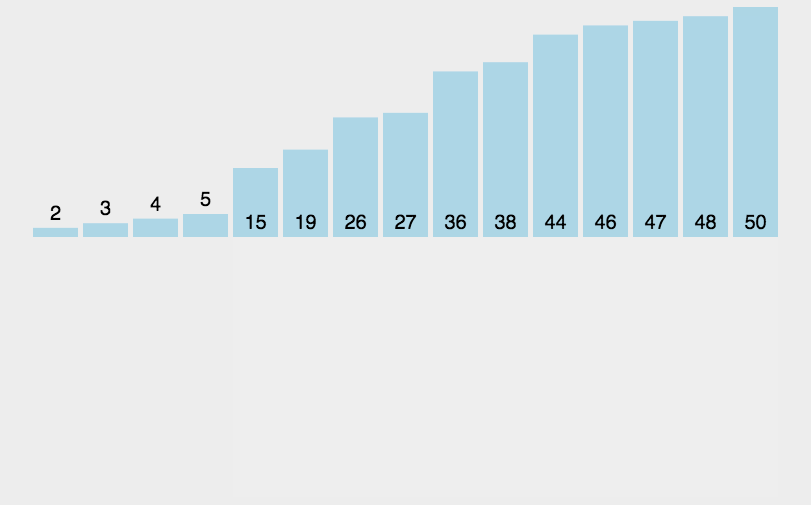
代码
//while 版本
void insert_sort(int *arr, int len)
{int j, tempVal;for (int i = 1; i < len; ++i)//从第二个数开始排{tempVal = arr[i];j = i - 1;while (j >= 0&&tempVal = 0 && tempVal < arr[j]; --j)arr[j + 1] = arr[j];arr[j + 1] = tempVal;}
}//while 版本
void insert_sort(int *arr, int len)
{int j, tempVal;for (int i = 1; i < len; ++i)//从第二个数开始排{tempVal = arr[i];j = i - 1;while (j >= 0&&tempVal = 0 && tempVal < arr[j]; --j)arr[j + 1] = arr[j];arr[j + 1] = tempVal;}
} 5.希尔排序(插入排序的优化)
原理:除二分组再插入排序
void shell_sort(int *arr, int len)
{int tempVal, j;int jump = len >> 1;//初始分组为长度的一半while (jump != 0)//组长不为0持续执行{//将插入排序的1改为组长for (size_t i = jump; i < len; ++i){tempVal = arr[i];for (j = i - jump; j >= 0 && tempVal < arr[j]; j-=jump)arr[j + jump] = arr[j];arr[j + jump] = tempVal;}jump >>= 1;}
}6.*快速排序
基本思想:分堆
划分标杆
小的数据分小堆,大的数据分大堆
一次确定一个
1.左右指针法
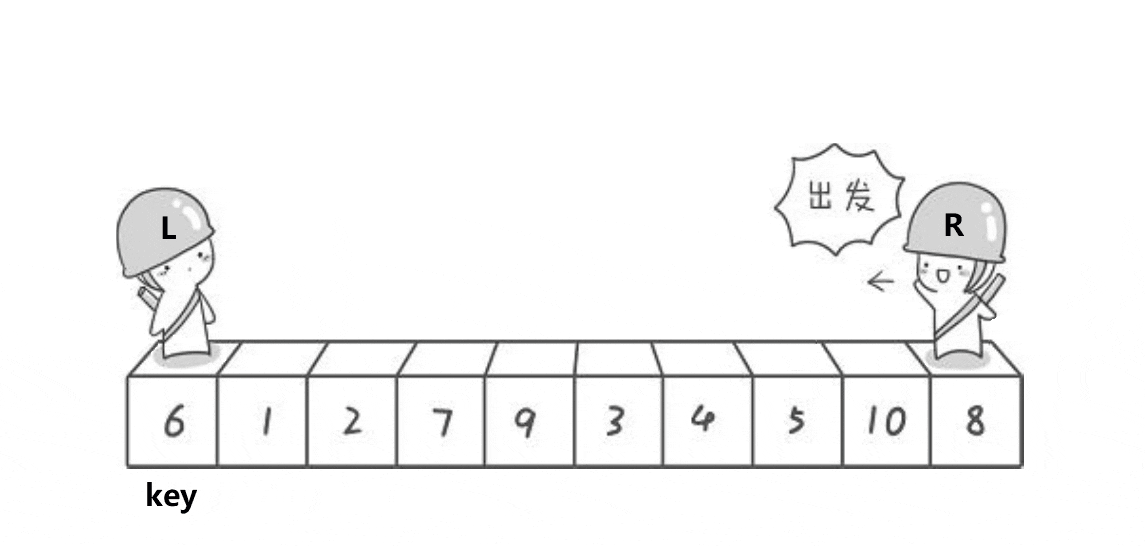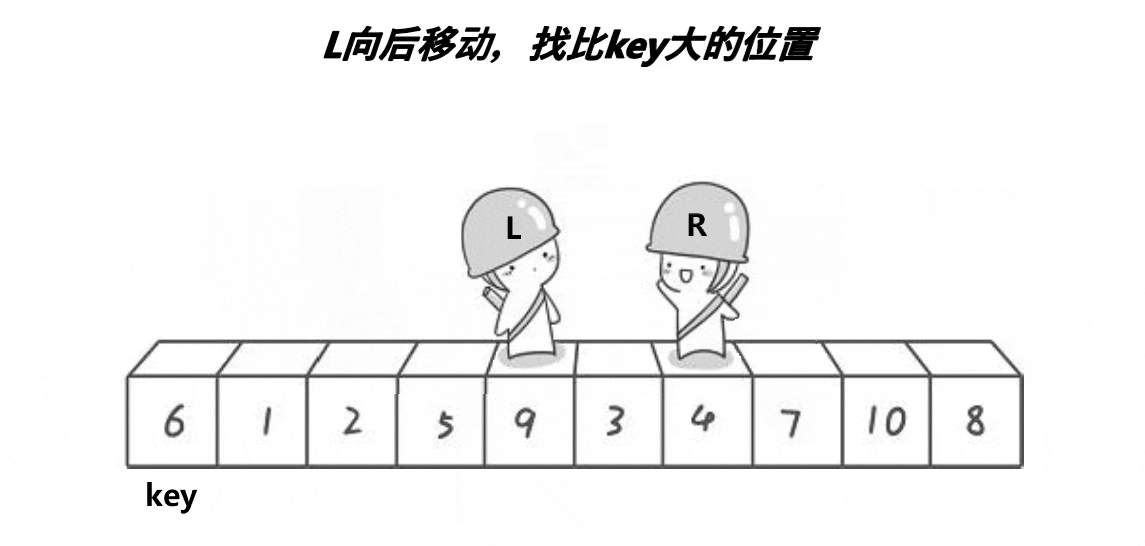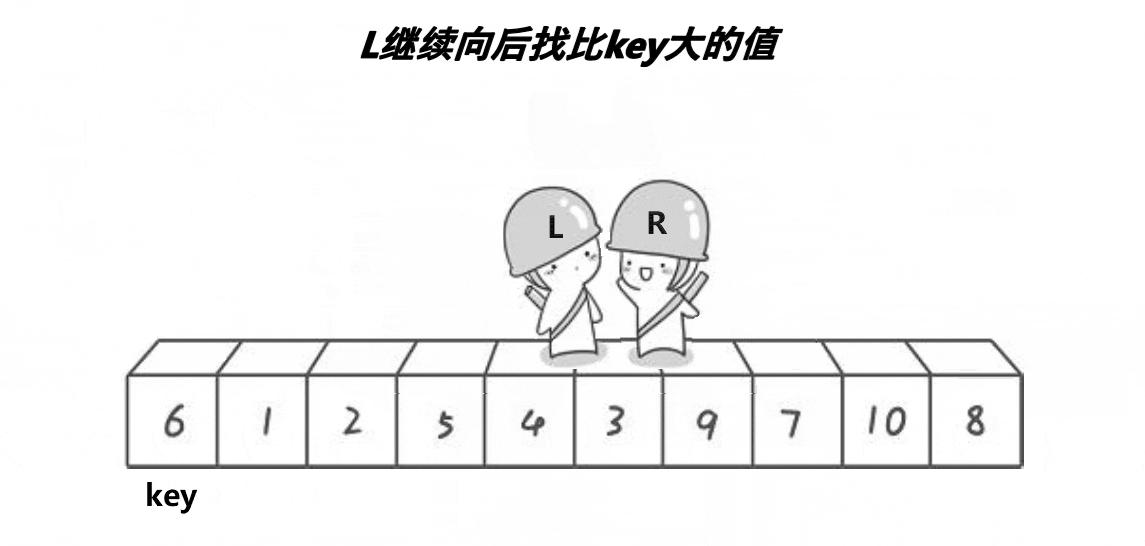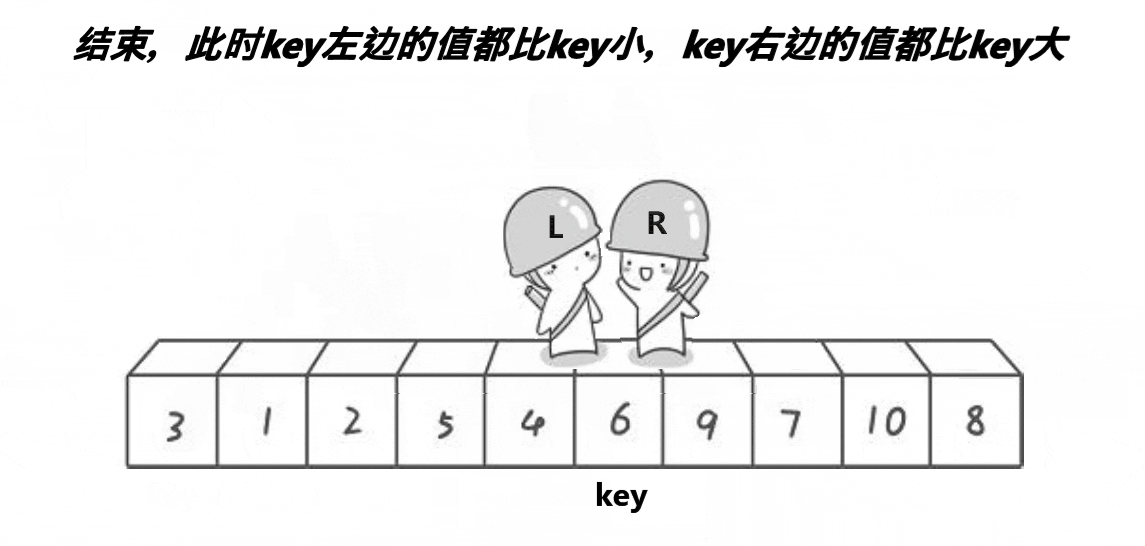
r小于l 区间存在
左指针遇到比自己小的往后走,遇到大的停下,右指针遇到比自己大的往前走,遇到小的停下,两数交换,最后标杆换位重置,递归执行
void _quick_sort(int *arr, int low, int hight);//换函数的声明
void quick_sort(int *arr, int len)
{_quick_sort(arr, 0, len - 1);//换函数
}void _quick_sort(int *arr, int low, int hight)
{int key = arr[low];//确定标杆int left =low +1, right =hight;//确定游标(索引)的值if (low >= hight)//说明区间只有一个元素,结束递归return;int temp;//数据交换//开始排序, 大前提 leftkey) right--;//交换if (left < right){temp = arr[left];arr[left] = arr[right];arr[right] = temp;/*arr[left] =arr[right]^arr[left];arr[right]=arr[right]^arr[left];arr[left]=arr[right]^arr[left];*/left++;right--;}}//完成分区,标杆归位arr[low] = arr[right];arr[right] = key;//递归左区间_quick_sort(arr, low, right - 1);//递归右区间_quick_sort(arr, right + 1, hight);} 2.挖坑法
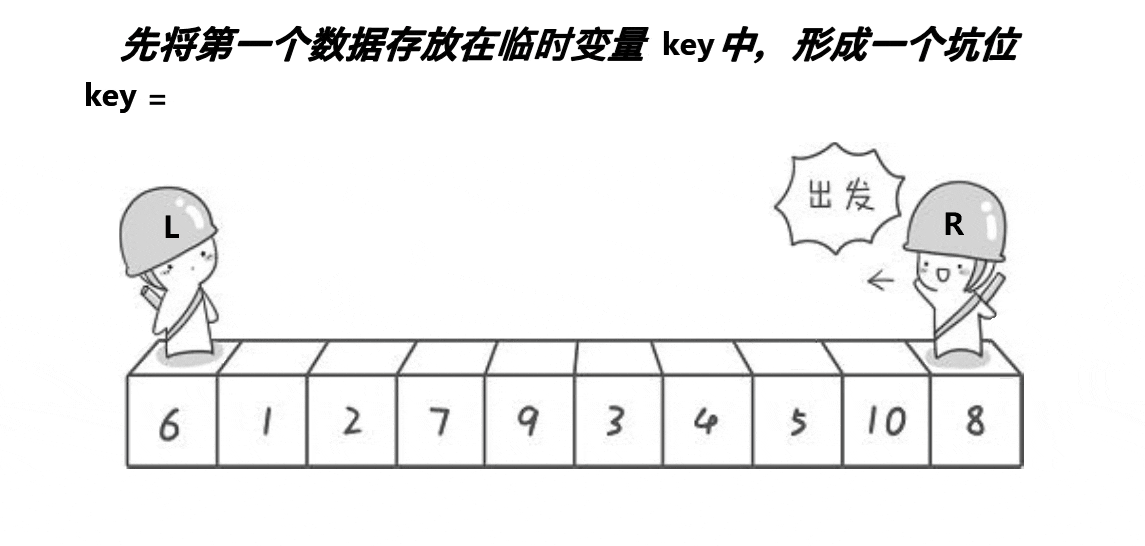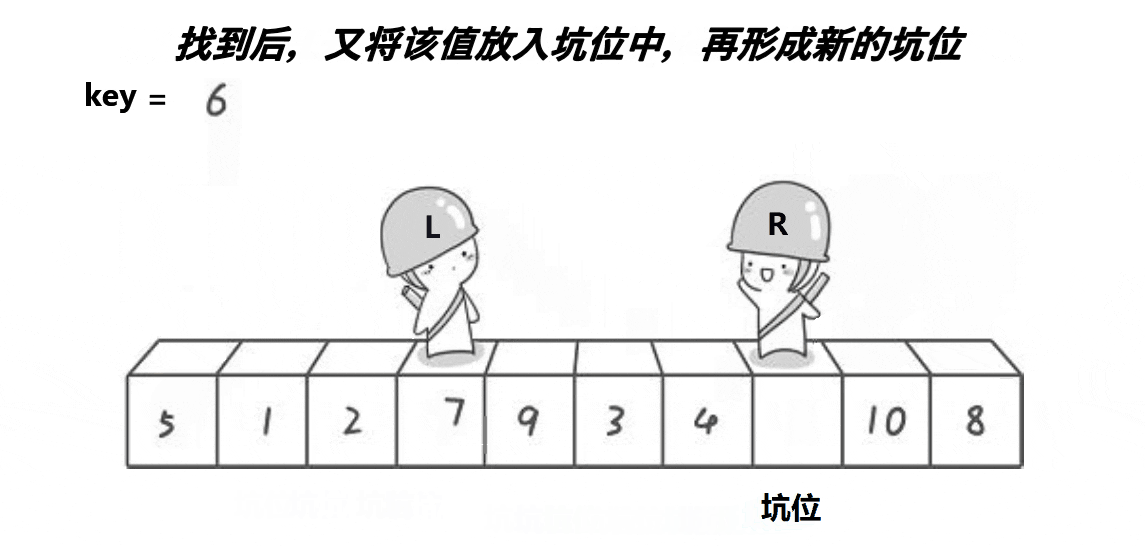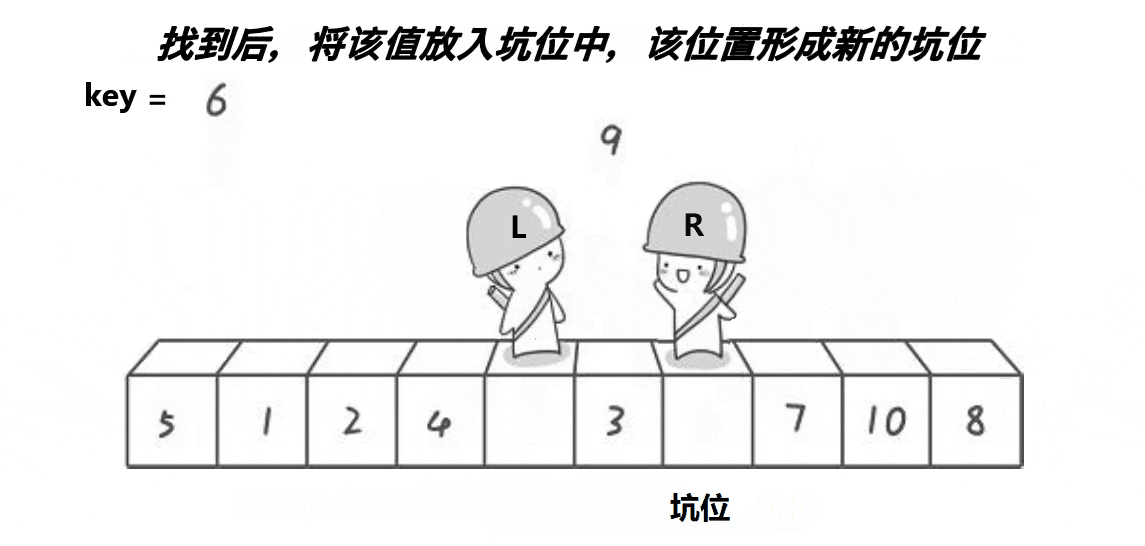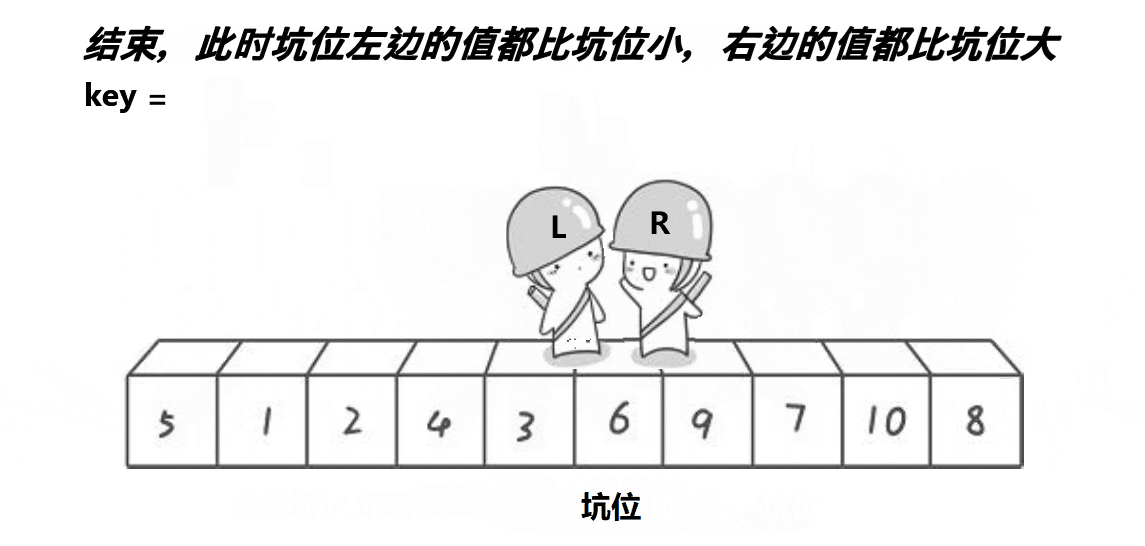
//快速排序法 挖坑法
void QuickSort1(int* arr, int begin, int end)
{if (begin >= end)return;int left = begin,right = end;int key = arr[begin];while (begin < end){//找小while (arr[end] >= key && begin < end){--end;}//小的放到左边的坑里arr[begin] = arr[end];//找大while (arr[begin] <= key && begin < end){++begin;}//大的放到右边的坑里arr[end] = arr[begin];}arr[begin] = key;int keyi = begin;//[left,keyi-1]keyi[keyi+1,right]QuickSort1(arr, left, keyi - 1);QuickSort1(arr, keyi + 1, right);
}7.基数排序(桶子法)空间复杂度利用最高
动画阐释各种排序算法(之前误删了大家也不用再点赞投币了)
原理:
第一轮除一%10
第二轮除10%10...
行存下数据
列往下遍历取出
全程没有进行数据的比较
1.准备桶子
2.初始化桶
3.循环放入
4.循环取出
void radix_sort(int *arr, int len)
{//准备桶子int temp[N][10] = {};int i, j, k,tempIdx;for (int n = 1; n < 10000; n *= 10)//步长 基于最大数的位数{//初始化桶for (i = 0; i < N; ++i){for (j = 0; j < 10; ++j){//初始化的值不会在数据里出现temp[i][j] = -1;}}//数据入桶for (i = 0; i < len; ++i){tempIdx = (arr[i] / n) % 10;temp[i][tempIdx] = arr[i];}k = 0;//数据出桶for (i = 0; i < 10; ++i){for (j = 0; j < N; ++j){if (temp[j][i] != -1)arr[k++] = temp[j][i];}}}
}
8.归并排序(分治法)
动画阐释各种排序算法(之前误删了大家也不用再点赞投币了)
递归再排序
先分后合
两两比较
代码实现:1.递归拆分
1.1 递归结束条件
1.2 递归左区间
1.3递归右区间
2.两路合并
2.1 准备一个辅助数组 两个游标
2.2 合并过程 - 两个数组至少遍历完一个
2.3 剩余部分拷贝进辅助数组
3.剩余拷贝进原数组
void _merge_sort(int *arr, int left, int right);
void _merge_in_arr(int *arr, int left, int mid, int right);
void merge_sort(int *arr, int len)
{_merge_sort(arr, 0, len);
}void _merge_sort(int *arr, int left, int right)
{// 递归结束条件if (left >= right)//说明区间只剩一个元素return;int mid = ((right-left) >> 1) + left;//递归左区间_merge_sort(arr, left, mid);//递归右区间_merge_sort(arr, mid + 1, right);//两路合并_merge_in_arr(arr, left, mid, right);
}void _merge_in_arr(int *arr, int left, int mid, int right)
{//每次合并数组长度不一致,动态规划int length = right - left + 1;//准备一个辅助数组 三个游标int *Pdata = new int[length];memset(Pdata, 0, sizeof(int)*length);int low = left;int hig = mid;int key = 0;//合并过程 - 两个数组至少遍历完一个while (low <= mid&&hig <= right){//左区间存在元素且比右区间小 落下while (low <= mid&&arr[low] < arr[hig]){Pdata[key++] = arr[low++];}//右区间存在元素且比左区间小 落下while (hig <= right&&arr[low]>arr[hig]){Pdata[key++] = arr[hig++];}}//出循环,则至少有一个数组落完 剩余部分拷贝进辅助数组if (low <= mid)//说明左区间还有东西memmove(&Pdata[key], &arr[low], sizeof(int)*(mid - low + 1));if (hig <= right)//说明右区间还有东西memmove(&Pdata[key], &arr[hig], sizeof(int)*(right - hig + 1));//剩余拷贝进原数组memmove(&arr[left], Pdata, length*sizeof(int));delete[] Pdata;
}本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!