0x30数学知识（更新中）

contents:

• 质数
• • Prime Distance poj2689
  • • 线性筛板子：
  • 阶乘分解
• 约数
• • 倍数法
  • 反素法
  • 余数之和
  • Hankson的趣味题
  • 互质与欧拉函数
  • Visible Lattice Points (POJ2090)
• 同余
• Sumdiv poj1845
• • 扩展欧几里得算法 Bezout
  • 用扩展欧几里得算法解线性方程ax+by=c
  • • 欧几里得的游戏
    • 青蛙的约会
• 矩阵乘法
• • 最幸运的数字
• 高斯消元与线性空间
• • 同余方程
  • 费马小定理
  • 欧拉定理
  • 乘法逆元
  • • exgcd求逆元
    • 费马小定理求逆元
  • 线性同余方程
  • • 同余方程
  • 中国剩余定理
  • • POJ1006 (Biorhythms)
  • 斐波拉契数 （待定系数法）
  • • 普通递归关系
    • 数字迷阵
• 组合计数
• • 离散对数
  • • 前缀知识 欧拉定理
    • 预备知识
• 容斥原理与mobius函数
• 概率与数学期望
• 0/1分数规划
• 博弈论之SG函数

质数

Prime Distance poj2689

链接: link.

线性筛板子：

bool st[N];
int primes[N], cnt;void get_primes(int n) {memset(st, 0, sizeof st);cnt = 0;for (int i = 2; i <= n; ++ i) {if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] * i <= n; ++ j) {st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}

阶乘分解

链接: link.

约数

倍数法

反素法

链接: link.

余数之和

链接: link.

Hankson的趣味题

链接: link.

互质与欧拉函数

欧拉板子
ll Euler(ll n){ll res = n;for(ll i = 2;i*i <= n;i++){if(n%i == 0) res = res/i*(i-1);//防止溢出while(n%i == 0) n /= i;}if(n > 1) res = res/n*(n-1);return res;
}

Visible Lattice Points (POJ2090)

链接: link.

//2~N的欧拉函数O(NlogN)

int phi[N];
void edler(int n){for(int i=2;i<=n;i++) phi[i]=i;for(int i=2;i<=n;i++)if(phi[i]==i)for(int j=i;j<=n;j+=i)phi[j] = phi[j] /i*(i-1);
}

//O(N)欧拉筛
有问题

int v[N], prime[N], phi2[N];
int m;
int sum2[N];void edler2(int n)
{memset(v, 0, sizeof(v)); //最小质因子m = 0;                   //质数数量for (int i = 2; i <= n; i++){if (v[i] == 0){ // i是质数v[i] = i, prime[++m] = i;phi2[i] = i - 1;}//给当前的数i乘上一个质因子for (int j = 1; j <= m; j++){// i有比prime[j]更小的质因子，或者超出n的范围，停止循环if (prime[j] > v[i] || prime[j] > n / i)break;// prime[j] 是合数i*prime[j]的最小质因子v[i * prime[j]] = prime[j];phi2[i * prime[j]] = phi2[i] * (i % prime[j] ? prime[j] - 1 : prime[j]);}}
}

同余

Sumdiv poj1845

https://www.acwing.com/problem/content/99/

扩展欧几里得算法 Bezout

int Extended_Euclid(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}int d = Extended_Euclid(b, a % b, x, y);int z = x;x = y;y = z - y * (a / b);return d;
}

用扩展欧几里得算法解线性方程ax+by=c

返回值是ab的GCD
顺便携带的值将xy也顺回来了

bool linearEquation(int a, int b, int c, int &x, int &y)
{int d = Extended_Euclid(a, b, x, y);if (c % d)return false;int k = c / d;x *= k; //+t*by *= k; //-t*a//求的只是其中一个解return true;
}

欧几里得的游戏

M,N
Stan开始，取其中较大的一个数，减去较小数的正整数倍，得到的数不能是0 ，然后Oile操作
直到一个人将得到一个0，win！
ex:
Stan: 25 7
Stan:11 7 {18 7,11 7,4 7均可能}
Oile:4 7
Stan:4 3
Oile:1 3
Stan: 1 0
Stanwin!
两人完美操作，谁会赢？
状态：
一：
50 18 50/18 = 2…14 初状态
32 18 末状态
二：
14 18 18/14 =1…4 初状态也是末状态
三：
14 4 14/4 = 3…2 初状态
10 4 中间状态
6 4 末状态
四：
2 4 4/2 = 2…0 末局

我们可以把一步辗转相除以及它与下一步辗转相除之间
的游戏状态称作“一局”，辗转相除的被除数和除数实际上对应了每一句的初状态。
显然，每一局的初状态是在游戏中必然出现的，而且最后一局只有一个状态，
面临最后一局初状态的人就赢得了胜利。
因此本题的大致想法是，尽量让自己能够去取每一局的初状态，让对手去取每一局（除了最后一局）
的末状态，下面就分两种情况来具体说明这个想法的实现。
第一种情况，先举个栗子，A= 32，B= 14，A和B的辗转相除过程如下
32/14=2…4
14/4=3…2
4/2=2…0
这种情况的特点就是：每一步相除所得的商都是大于1，即对于每局的初状态(A,B),
A>B,都满足：A div B > 1 ,对于这种情况，我们的策略是取走（A div B -1) * B ,这样就得到新状态（A mod B + B ,B）,接下来，对手就没有选择，只能取走B，剩下（A mod B,B）,而这就是下一局的初状态，这样就保证下一局的初始状态肯定由自己取，这种情况下Stan必胜
第二种情况是某一局的初始状态满足A div B = 1 ，即这一局只有一个状态，自己取完之后下一局状态必然落在对方手里。
以下是这种情况的一般性表述，存在连续的若干局Pi(Ai,Bi),…Pj(Aj,Bj) i + 1 < j ,A_i div B _i > 1
且对于任何一局 P_k （Ak，Bk）.ikdiv B_k = 1 如果 j-i是奇数，则P_j 和P_i 的初状态的持有人相同，如果j-i 是偶数，则不同，因此，如果出现了j-i 是偶数，就有必要在P_i 局势中一次性取光，即把下一局的状态拱手相让，这样就可以保证在P_j 局中再一次拿到初状态。
总之就是，首先拿到A div B > 1 状态的人是必胜的， 总能够根据两种情况作出正确的选择，从而在最后的局中拿到初状态，因此首先拿到AdivB>1初状态的人是必胜的，但如果出现从初始转态开始，每一局都是AdivB = 1 ex:24 15(15 9, 9 6, 6 3,3 0)则要根据这样的局数来判断输赢。

#include 
using namespace std;
int main()
{int t;cin >> t;while (t--){int m, n;cin >> m >> n;if (m < n)swap(n, m);int f = 1;while (m / n == 1 && m % n){int t = m%n;m = n;n = t;f = -f;}if(f==1) cout<<"Stanwins"<<endl;else cout<<"Oilewins"<<endl;}
}

青蛙的约会

链接: link.
两个青蛙跳到同一个点上才算是遇到了，所以可以推出如下式子：
(x+mt) - (y+nt) = p L
其中：t是跳的次数，p是a,b青蛙跳的圈数之差，整个就是路程差等于纬度线周长的整数倍
转化一下，（n-m）t + Lp = x-y
令:a=n-m ,b = L,c = GCD(a,b) ,d = x-y
有：at+bp=d
要求的是：t的最小整数解
用扩展欧几里得求出其中一组解 t0、p0 ，并令c = GCD(a,b)
有：at0+bp0=c
因为：c = GCD(a,b)，所以：at/c ,bt/c也是整数，所以d/c也需要是整数，否则无解
两式同时乘以（d/c） ，得到：at0* (d/c) + b*p0 * (d/c) = d;
所以：t0/(d/c)是最小的解，但有可能是负数
因为：a * ( t0 * (d/c) + b * n) + b * ( p0 * ( d / c) = d
所以，解为（ t0 * ( d / c ) % b + b ) % b

#include 
using namespace std;int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}int gcd = exgcd(b, a % b, x, y);int t = x;x = y;y = t - a / b * y;return gcd;
}int main()
{int nok = 0, x, y, m, n, l, X, Y, gcd;cin >> x >> y >> m >> n >> l;if ((x - y) % (gcd = exgcd(n - m, l, X, Y)) != 0)cout << "Impossible" << endl;elsecout << ((long long)(x - y) / gcd * X % (l / gcd) + (l / gcd)) % (l % gcd) << endl;return 0;
}

矩阵乘法

最幸运的数字

链接: link.

高斯消元与线性空间

同余方程

链接: link.

费马小定理

链接: link.

欧拉定理

乘法逆元

若 a * x 同余 1（mod m） ,a,b互质。则称x为a的逆元，记为a^-1
根据逆元的定义，可转化为ax+by=1，用扩展欧几里得法求解。逆元可以利用来计算（t/a）mod b 时，转化为 t*a^-1、 mod b
利用快速幂及扩展欧几里得算法求逆元的代码如下：

exgcd求逆元

ll exgcd(ll a, ll b, ll &x, ll &y)
{if (b){x = 1, y = 0;return a;}ll res = exgcd(b, a % b, x, y);ll tmp = x;x = y;y = tmp - a / b * y;return res;
}
ll exgcd_inv(ll a, ll n) //扩展欧几里得求逆元
{ll d, x, y;d = exgcd(a,n,x,y);return d ==1 ?(x+n)%n:-1;//没有逆元返回-1
}

费马小定理求逆元

ll pow_mod(ll a, ll b, ll key) //
{ll tmp = b;for (; a; a >>= 1, tmp = (tmp * tmp % key))if (a & 1)tmp = (tmp * b % key);return tmp;
}
ll fermat_inv(ll a, ll n) //费马小定理求逆元
{return pow_mod(a, n - 2, n);
}

9

线性同余方程

给定整数a,b,m,求一个整数x满足ax 同余 b(mod m) ,或者给出无解，因为未知数的指数为1，所有我们称之为一次同余方程，也称线性同余方程。
ax 同余 b(mod m) 等价于 ax - b 是m 的倍数，不妨设为 -y 倍，于是，该方程可以改写为 ax+nmy = b
根据Bezout 定理及其证明过程，线性同余方程有解当且仅当gcd(a,m )|b
在有解时，先用欧几里得算法求出一组整数x0，y0,满足 a * x0 + my0 = gcd（a,m）. 然后 x = x0 * b /gcd(a,m) 就是 原线性同余方程的一个解
方程的通解则是所有 模 m/gcd（a,m） 与x同余的整数

同余方程

链接: link.

#include 
using namespace std;
#define ll long long
#define db double
#define pii pair<int, int>
#define psi pair<string, int>
#define ull unsigned ll
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#define ld long double
const int N = 1E5 + 7;
#define INF ~0ULLint exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}int d = exgcd(b, a % b, x, y);int z = x;x = y;y = z - y * (a / b);return d;
}
int main()
{int a,b;cin>>a>>b;int x,y;exgcd(a,b,x,y);cout<<"a"<<a<<"b"<<b<<"x"<<x<<"y"<<y<<endl;cout<<(x%b+b)%b<<endl;return 0;
}

中国剩余定理

#include <bits/stdc++.h。
using namespace std;int exgcd(int a, int b, int &x, int &y)
{if (b == 0){x = 1, y = 0;return a;}int d = exgcd(b, a % b, x, y);int z = x;x = y;y = z - y * (a / b);return d;
}int China(int W[], int B[], int k) // W为按多少排列，B为剩余个数，W>B,k为组数
{int x, y, a = 0, m, n = 1;for (int i = 0; i < k; i++){n *= W[i];}for (int i = 0; i < k; i++){m = n / W[i];exgcd(W[i], m, x, y);a = (a + y + m * B[i]) % n;}if (a > 0)return a;elsereturn a + n;
}

POJ1006 (Biorhythms)

链接: link.

23,28,33
S = N1+T1k1=N2+T2k2=N3+T3*k3;
N为出现峰值的日期，T为周期，我们要求出k,使得上式子成立
逆推：S满足三个条件，除以T为N,求最小数,满足上述条件

#include 
using namespace std;
int main()
{int p, e, i, d, T = 1;cin >> p >> e >> i >> d;do{int lcm = 21252;//lcm(23,28,33);int ans = (5544*p+14421*e+1288*i-d+lcm)%lcm;if(ans==0) ans = lcm;cout<<"Case "<<T++<<": the next triple peak occurs in "<<ans<<" days. "<<endl;cin>>p>>e>>i>>d;}while(p!=-1);return 0;
}

链接: link.

斐波拉契数 （待定系数法）

链接: link.

普通递归关系

https://blog.csdn.net/weixin_43870114/article/details/90673734

数字迷阵

https://blog.csdn.net/zyg0121/article/details/68954009
https://blog.csdn.net/weixin_43826249/article/details/103892845

组合计数

离散对数

前缀知识 欧拉定理

对与任意的a,m,只要gcd(a,m)=1,那么就有， a^φ(5) 三 1（mod m）

预备知识

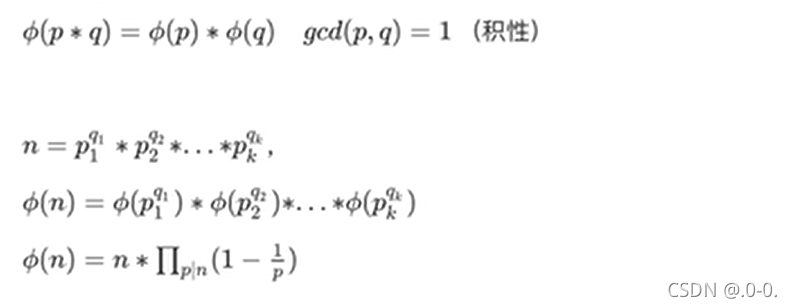
容斥原理与mobius函数

概率与数学期望

0/1分数规划

博弈论之SG函数

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！