「管理数学基础」2.1 泛函分析：距离空间及其完备性

距离空间及其完备性

文章目录

• 距离空间及其完备性
• • 距离与距离空间
  • • 定义：距离
    • 例题1：是否为距离
    • 例题2：是否为距离
    • 定义：距离空间
    • 例题3：讨论以下定义是否为距离
  • 距离空间的完备性
  • • 定义：点列的极限
    • 定义与性质：柯西列
    • 完备性
    • • 重要定理：R1柯西列完备
      • 例题4&5：证明距离空间完备
      • 例题：证明离散距离空间是完备的

• 空间：赋予了某种数学结构的非空集合
• 算子：两个集合间的映射

距离与距离空间

定义：距离

分析：

• 判断是否为距离，即判断$d$是否满足上述三个性质
• 是任取$x,y\in X$
• 一般可以用“$d(x,y)=0$但$x\ne y$”来反证不是距离
• 此外，也可以用特殊的$(x,y,z)$带到三角不等式里面，举反例

例题1：是否为距离

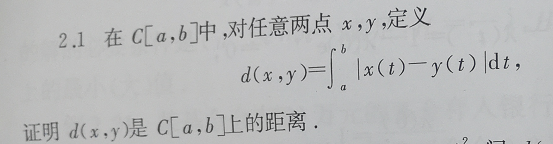
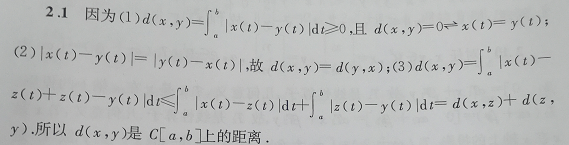
分析：

• 依次检验三条性质即可
• 答案写得不标准，应该有任取$x,y\in C[a,b]$

例题2：是否为距离

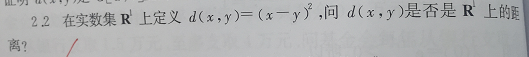
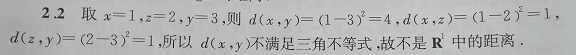
分析：利用了反例，三角不等式。

定义：距离空间

定义了距离$d$的非空集合$X$，称为距离空间，可简记为$(X,d)$。

例题3：讨论以下定义是否为距离

(1) 易征，略。

(2) 的第三条性质“三角不等式”需要额外推导一下。

分析：为了引出$d(x,y)$与$z$的关系，特意设定了如上我用红框标注的关系： a i = x i − z i a_i = x_i - z_i ai​=xi​−zi​， b i = z i − y i b_i = z_i - y_i bi​=zi​−yi​。

(3)

有句话值得琢磨：由(2)、(3)可见，在同一空间 R n R^n Rn上，可以定义不同的距离（ ∑ i = 1 n ( x i − y i ) 2 \sqrt{\sum_{i=1}^n (x_i - y_i)^2} ∑i=1n​(xi​−yi​)2 ​和 ∑ 1 n ∣ x i − y i ∣ \sum_1^n |x_i - y_i| ∑1n​∣xi​−yi​∣），从而构成不同的距离空间。

上述这句话码提示了我们：距离空间与距离密切相关，距离定义了距离空间。

(4)

分析：

• 这个值得注意，这里的距离不是两个点的距离，而是两个函数的距离
• 注意， min ⁡ a ≤ t ≤ b ∣ x ( t ) − y ( t ) ∣ = 0 \min_{a\le t \le b}|x(t) - y(t)|=0 mina≤t≤b​∣x(t)−y(t)∣=0中，这个$\min$是针对$t$而言的
  • 这就是说只要有一处 t = t 0 t=t_0 t=t0​，使得 x ( t 0 ) = y ( t 0 ) x(t_0)=y(t_0) x(t0​)=y(t0​)，那么就会有 min ⁡ a ≤ t ≤ b ∣ x ( t ) − y ( t ) ∣ = 0 \min_{a\le t \le b}|x(t) - y(t)|=0 mina≤t≤b​∣x(t)−y(t)∣=0，如上图两条曲线有一个交点
  • 但这就与“$d(x,y)=0$互为充要条件$x=y$”不符合，因为$x(t)$与$y(t)$只在 t = t 0 t=t_0 t=t0​处相等，并非$x(t)=y(t)$两个函数相等

(5)

距离空间的完备性

定义：点列的极限

定义与性质：柯西列

分析：

• 点列收敛，一定是柯西列（证明中利用了距离的性质）
• 柯西列不一定收敛
• 柯西列可以理解为两个点都向远处跑，二者距离为0（ d ( x n , x m ) → 0 ; m , n → ∞ d(x_n,x_m)\to 0;m,n\to \infty d(xn​,xm​)→0;m,n→∞）

例子：是柯西列，但是不收敛。

如上两个例题，并没有说该柯西列不收敛到某个数，而是收敛后不属于该空间了。因此说，不收敛。

完备性

定义：若$X$中任意柯西列均收敛，则称$(X,d)$是完备的距离空间。即：$X$对极限运算封闭。

即：柯西列在该空间收敛，该空间完备。

重要定理：R1柯西列完备

这个在证明完备性的例题种很常用。

例题4&5：证明距离空间完备

例题4

例题5

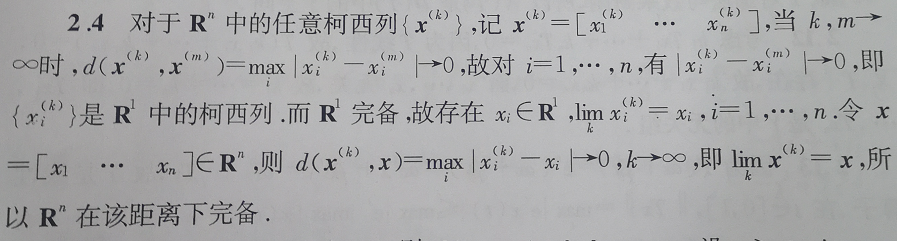
分析：

• 先证明是柯西列
• 再任取一个维度，利用 R 1 R^1 R1完备的特点，得出 lim ⁡ k x i ( k ) = x , i = 1 , . . . , n \lim_k x_i^{(k)}=x,i=1,...,n limk​xi(k)​=x,i=1,...,n
• 再带回去得到 x = ( x 1 , . . . , x n ) T ; d ( x k , x ) → 0 ; k → ∞ x=(x_1, ..., x_n)^T;d(x_k,x)\to 0;k\to \infty x=(x1​,...,xn​)T;d(xk​,x)→0;k→∞

例题：证明离散距离空间是完备的

分析：

• 因为是离散距离空间，因此如果二者$d\to 0$
• 则说明两个点也相等，则有 x m = x k x_m = x_k xm​=xk​
• 那这里可以按住一个点，比如设$m>k$，按住$k$， x k x_k xk​则为收敛判定 lim ⁡ k x m = x k ; m → ∞ \lim_k x_m=x_k;m \to \infty limk​xm​=xk​;m→∞中的常数

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！