基于物理渲染的实时渲染材料(表面模型) ------计算机图形学高质量实时渲染(九)

基于物理渲染的实时渲染材料(表面模型)

Real-Time Physically-Based Materials（Surface models）

本节内容：

• Microfacet BRDF（微表面模型）
• Disney Principled BRDF
  
  

LTC：在不考虑遮挡和阴影情况下做微表面模型的shading。

Real-Time Physically- Based Materials

我们首先来看一下Physically-Based Rendering 的字面意思：

基于物理的渲染

• 渲染内部的任何话题都应在PBR范围之内
• 例如材质（materials)、光照（lighting）、相机（camera）、光线传播（light transport）等等
• 因此PBR在概念上来说不只限制在材质上，但是在RTR中我们提到PBR指的就是PBR材质

实时渲染中的PBR(材质)

实时渲染在材质方面的丰富程度要远远落后于离线渲染

• 一方面是种类，例如离线渲染中artist可以找出几百种材质，而在RTR中则有十几种，因为要考虑到速度和研究透彻的程度
• 另一方面是准确度/质量比起离线渲染较差，因为为了让这种材质快速的被渲染，我们需要牺牲较大的质量效果.比如：毛发的渲染，毛发由于它的超级复杂性，一是毛发根数众多，如果模拟每根毛发的light transport那将是一个巨大的计算量会拖慢渲染速度；实时渲染是在保证速度的前提下，尽可能的提升质量（RTR中速度是首要的）
• “PB”在实时渲染中由于做了大量的简化来保证速度，因此严格来说基本都不是基于物理（Physically-Based）的

实时渲染中的材质分类

我们将其分成两类：

1.基于物体表面上定义的材质(绝大多数材质)

基于物体表面又分为两种：

• Microfacet Models微表面模型（有时候并不是完全基于物理的）
  
• Disney Principled BRDF计算量比较轻量级，因此虽然产生初衷是为了能够用于离线渲染,但也可以运用在实时渲染中，这套材质的种类多效果也很不错,但也不是PBR，是基于artist的角度来考虑的。
  

2.基于体积上定义的材质

由于光线会进入到云，烟，雾，皮肤，头发等体积里，但是在RTR中基于体积要比基于表面的困难许多，我们大部分考虑的还是光线在这些体积中作用一次（single）和多次（multiple）的分离考虑方法，这个在下节课学习。

• 1.对于PBR来说，在RTR并没有什么新理论，我们所用的都是离线渲染中仍在使用的，但是放在RTR中就会变得开销巨大
• 2.因此再RTR中我们更多的是考虑用来解决问题的Hacks方法，还是那句话，RTR中速度是首要的，我们要在保证速度的前提下去尽可能的提高渲染质量。

Microfacet Models微表面模型

接下来开始我们进入Microfacet models微表面模型，首先我们来回顾一下101中的一些微表面的知识：

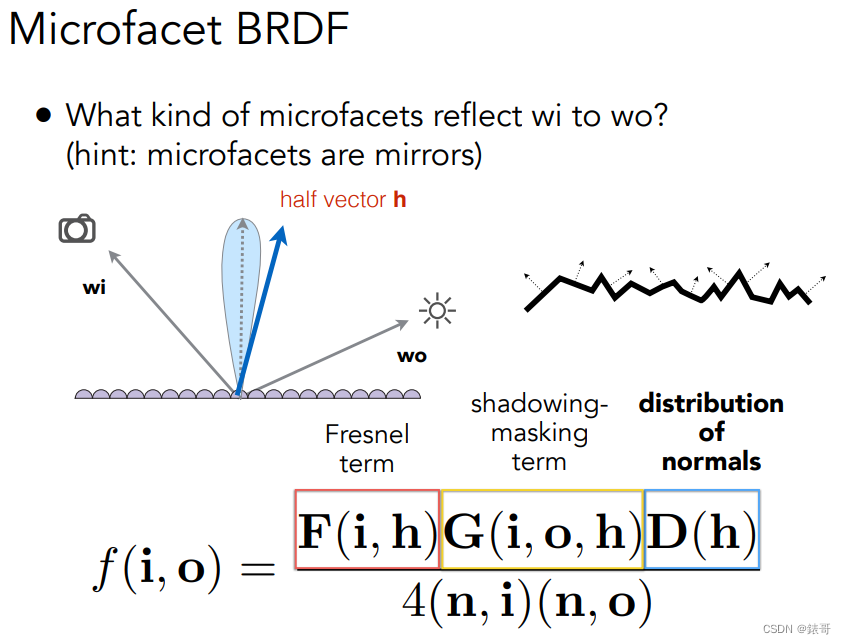
什么是微表面BRDF?

我们认为在宏观上看上去是平的，但是在微观上看去会看到各种各样的微表面，这些微表面的朝向，也就是法线各不相同，这些微表面法线的分布导致的渲染出的结果各不相同。

微表面BRDF中有几个至关重要的项：

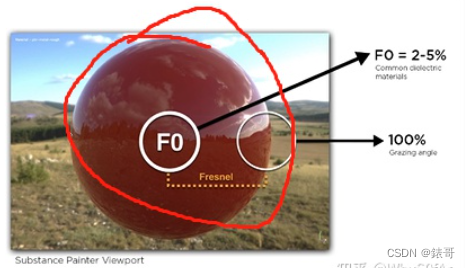
1.F项：菲涅尔项

表示入射角度不同，反射光所占的比例。

有多少能量被反射取决于入射光的角度，当入射方向接近grazing angle掠射角度时，光显示被反射的最多的，也就是当你的入射角度与法线几乎垂直时，反射的radiance是最多的。

由于光路的可逆性，我们可以认为眼睛看过去的方向是光线入射方向。

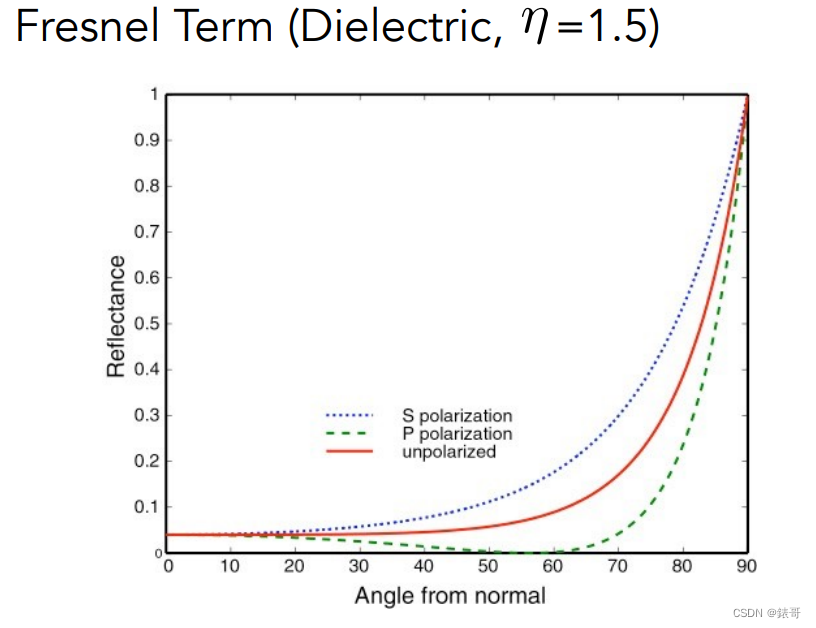
下面是对于绝缘体反射率与角度的关系：

以河面为例，让你入射方向与河面法线平行，则会直接看到河底；如果入射方向与河面法线垂直，则能最大程度看到反射出的天空之类的。

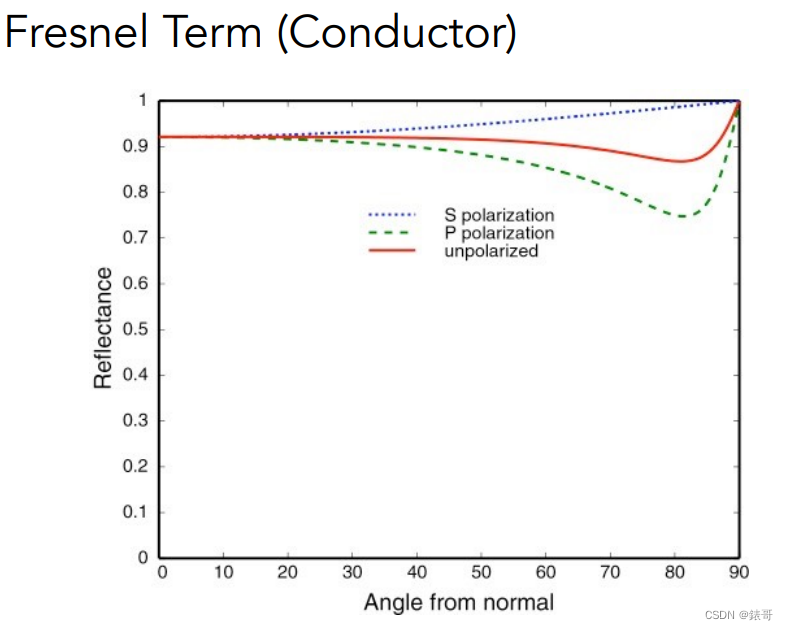
下面是对于道题反射率与角度的关系，与绝缘体不同，部分会出现反常现象。

菲涅尔项告诉我们有百分之多少的能量会被反射出来。

菲涅尔项的推导要考虑光线的S极化和P极化效果，公式比较复杂，因为要考虑不同介质，如从空气到物体表面，各自的折射率和入射角折射角，最终推导出下图中的公式。

但我们平常不用这个，而是用一个简单的近似：Schlick’s approximation(施利克近似)

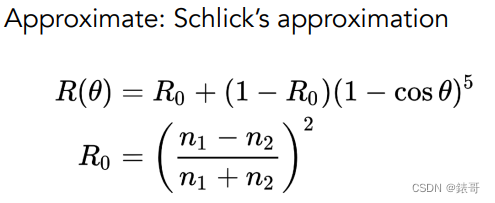
我们之前讲过：

当θ->90度，cosθ=0，则R(θ)=1；
当θ->0度，cosθ=1，则R(θ)=R0；

其中R0（基础反射率）取决于物体，不同物体的R0各不相同。金属一般为0.04

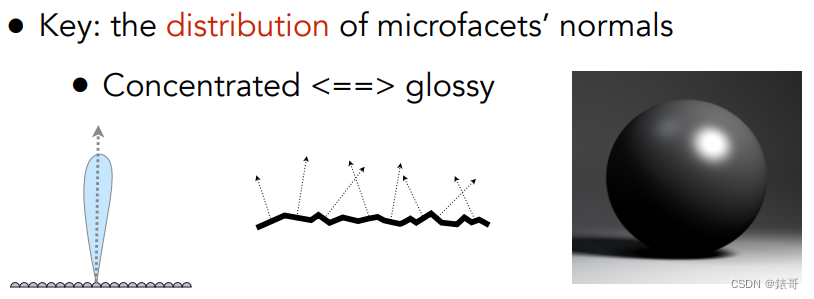
2.D项：法线分布函数

决定这一项的是不同微表面朝向的法线分布；
当朝向比较集中的时候会得到Glossy的结果，如果朝向特别集中指向时认为是speular的。

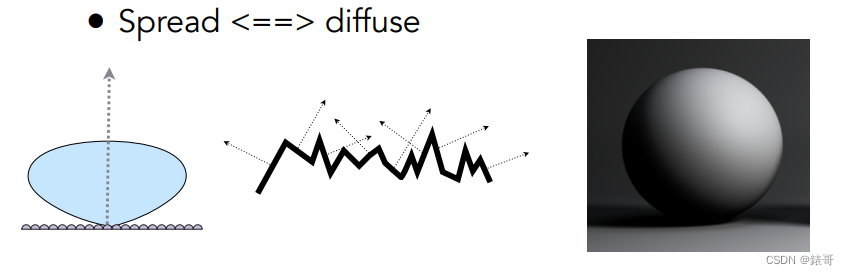
当分布杂乱无章的时候，因此认为表面也非常复杂，得到的结果也就类似diffuse的.

当NDF变得十分复杂时，我们可以这么理解，从glossy变为diffuse的，我们认为把glossy物体围观的高度场拉大，导致微观上的表面们变得倾斜（做了一个scale），从而让之间的沟壑变深且改变法线分布朝向，从而成为diffuse的。


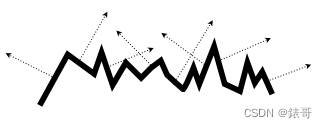
NDF–>Normal Distribution Function

1.我们把为表面法线分布的函数定义为normal distribution function（NDF）

2.我们有很多不同的模型来描述法线分布：

• 常用的Beckmann，GGX等等模型；
• 闫令琪自己的一系列模型（2014,2016,2018）
  

我们主要讲Beckmann和GGX这两个NDF模型

Beckmann模型

为了描述法线分布，肯定是一个对于微表面的法线方向（半程向量方向）h的函数，h是半球上任一方向，为了描述这一方向对应的值是多少我们需要NDF。

我们来深入理解一下这个函数：

这个函数可以描述不同粗糙程度的表面，不同粗糙程度的意思是NDF中lobe是集中在一个点上，还是分布的比较开。

我们想一下高斯函数中用σ来控制胖瘦，也就是标准差，同样对应到D(h)中：

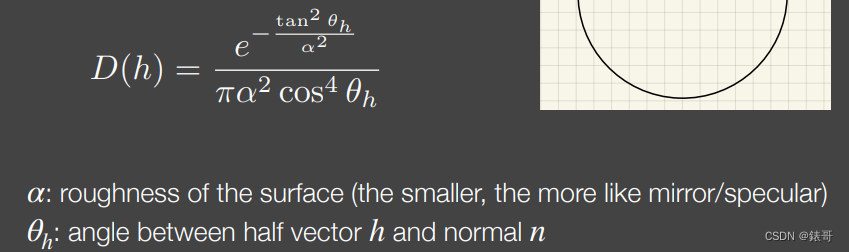
α描述的是法线粗糙程度，粗糙程度这个值越小，表面就越光滑。
θh：微表面半程向量法线与宏观表面法线(0,0,1)方向n的夹角。
到现在为止发现定义只与θ有关，与φ无关，因此描述的是各向同性的结果，也就是沿着中心旋转是相同的结果。

分子上面为什么用tanθh，而不用θh？

因为是定义在slope space坡度空间上的：

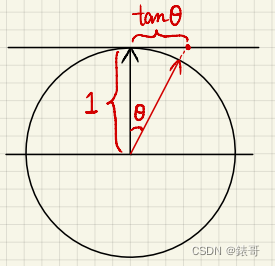
tanθh与θh的关系如图所示，一维中tanθ就是法线延长到切线交点到宏观法线顶端的距离，二维中则是与切表面的交点到宏观法线顶端的距离。
在tanθ上的定义一个高斯函数，也就是在切平面这么一个无限大平面上定义一个高斯函数，在平面上定义和在角度上定义的含义差不多。
由于高斯函数的定义域是非常大的，但在过了3α后会缩减到非常小但不是0，为了满足这一性质定义在坡度空间，因为虽然距离非常远，但是一定对应着单位球（圆），上一个有限角度，从而保证slope space中无限大的函数无论如何也不会出现面朝下的微表面。

因为如果你定义在θ的一个高斯，无论用多小的高斯，当θ超过90度，仍然会有值，但是定义在slope space上则不会出现这一情况，从而保证微表面不会朝下，但是无法避免反射光朝下

GGX模型(TR模型)
Beckmann模型的NDF曲线与GGX模型的NDF曲线相比有一个明显的缺点 ：
long tail 长尾性质：
会很快衰减，但是衰减到一定程度的时候，衰减速度就会变慢，可以看到即使到了grazing angle（90度）时仍不为0.

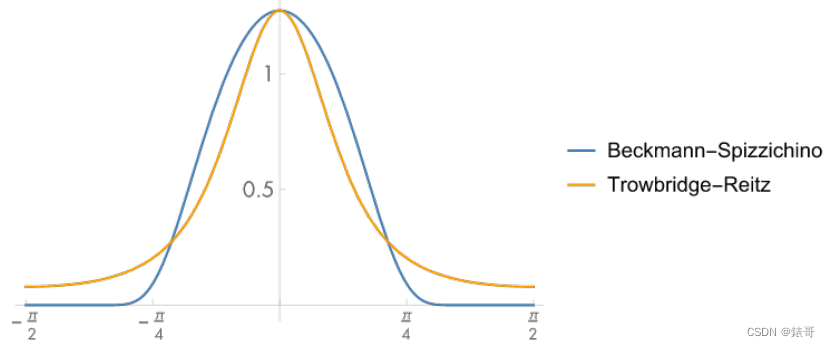
这会带来两个好处：

• 1.beckmann的高光会逐渐消失，而GGX的高光会减少而不会消失，这就意味着高光的周围我们看到一种光晕现象。
• 2.GGX除了高光部分，其余部分都有diffuse的感觉。
  

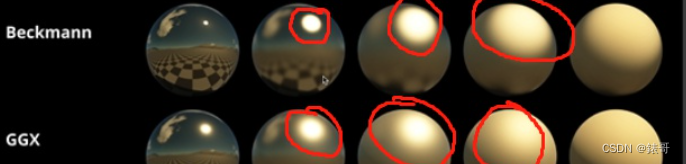
beckmann模型与GGX模型的实际效果对比如图。

相同的粗糙程度下GGX的效果更加自然，因为long tail特性导致高光到非高光有一个柔和的过渡状态，而非Beckmann的高光到达grazing angle后戛然而止，我们希望的是像GGX一样的效果。

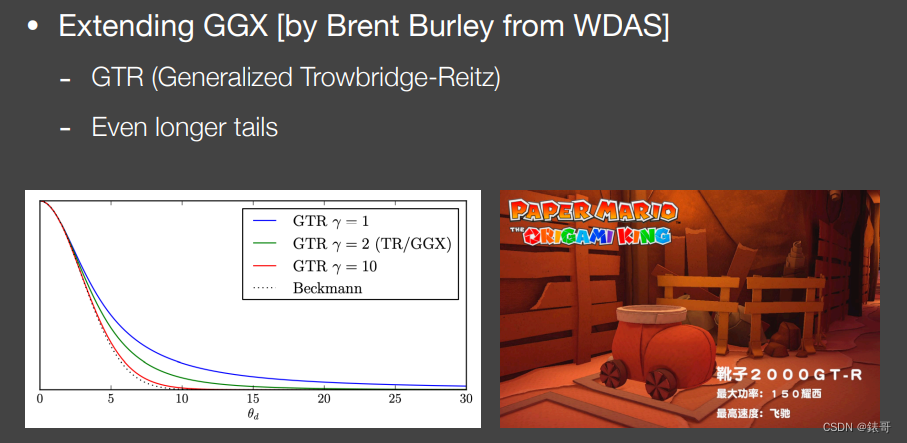
GGX模型的扩展
GTR（Generalized Trowbridge-Reitz），多了参数γ，根据γ不同可以调节拖尾长度；

• 包括了本身GGX，当γ=2时候就是GGX，当γ超过10会接近Beckmann；
• 具有更长的拖尾。
  

3.G项：shadowing-Masking（也是非常重要的一项）

shadowing -Masking有另外的一个名称->Geometry Term，这也是缩写为G的原因。

解决的问题就是微表面之间的自遮挡问题，尤其是在角度接近grazing angle时。

如图，由于在微观上有不同的微表面，因此虚线部分本该入射的光被遮挡了，由于光线时可逆的，因此不只是看过去被遮挡，往外看时也被遮挡。

分为两种情况：
左边这种从light出发发生的微表面遮挡现象叫做shadowing
右边这种从eye出发发生的微表面遮挡现象被称为masking；

我们之所以引入G项就是为了考虑由于遮挡产生的darkening现象（由于微表面自遮挡，因此实际计算出的结果会比理想结果亮，所以加上G项使得结果变暗接近理想结果）

因此由于在接近grazing angle时遮挡现象最大也就是接近于0，垂直看向时无遮挡也就是1.

** 那么在不考虑G项时，在掠射角度会发生什么情况？**

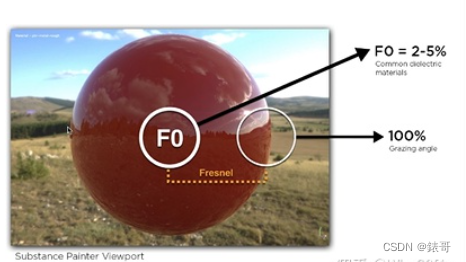
我们以图为例，我再次假设我们从grazing angle处看向F0旁边的白圈里的点，即我们的观察方向与表面法线接近垂直，我们代入公式考虑：

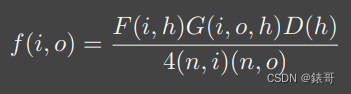
当在grazing angle处时，F则=1，不考虑G项，那G项=1，D是一个法线分布，是一个正常的函数没有什么特别大的值，到此分子部分考虑完毕。
我们来考虑一下分母，分母中存在的两个法线与入射方向（n，i）法线与出射方向（n，o）的点乘，当在grazing angle时入射方向、出射方向与法线角度接近90°，因此点乘结果会非常小接近0，分子除以一个接近于0的值会导致结果变得巨大，就会导致我们看到的这张图整个外圈是白的。

引入G项，shadowing-masking项也就是为了避免这种情况产生的
常用的The Smith Shadowing - Masking项：
在the Smith shadowing-masking 中，我们把shadowing 和masking分开考虑

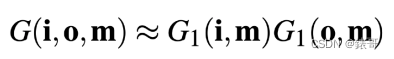
我们看下面这张图，绿线是GGX,红线是beckmann。

在两种不同NDF下预测出的G项有一些细微差别但其实相差不大，垂直入射的时候shadowing-masking不起作用，在grazing angle时，G项变得非常小接近于0，从而我们解决了分子除以分母导致函数结果过大，整体发白的问题。

我们来举一个很简单的例子

• 未添加G项前 = 1/0.4 =2.5
• 添加G项后 = 0.6/0.4 = 1.5
  很显而易见的再添加了G项后整体的值变小解决了外圈发白的问题
  
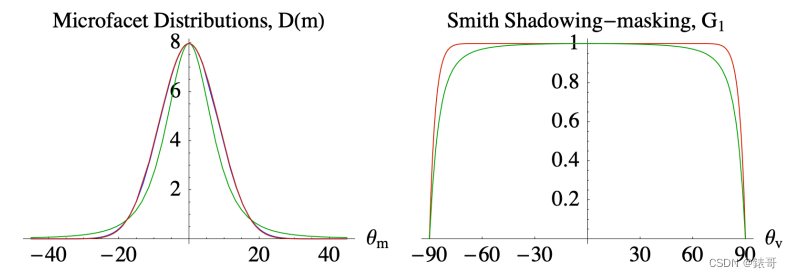
  但是在我们正确的考虑了D、F、G三项后，仍然存在一些问题：
  
  在这个图中，没有发现任何grazing angle的问题，但是随着粗糙程度变大，我们渲染得到的结果却越暗，即使认为最左边是抛光，最右边的是哑光，这个结果也是错误的，因此再怎么哑光也不能让白金变成跟石头一样的光泽。

如下图，在uniform的环境光照下即是物体再粗糙我们再这样的光照下得到的结果也应该都是接近于背景的一个颜色，而不是这种

这时候因为由于没有考虑光线在表面上的多次弹射，只考虑了微表面遮挡的情况，当粗糙度越来越大的时候，能量是不守恒的，因此才导致了粗糙度增大引起能量损失这一现象。

当表面越粗糙时，反射光更容易会被表面挡住，同时越粗糙的表面在表面之间弹射的次数越多，我个人理解闫老师所说的G项是只考虑了一次Bounce，因此当只考虑依次弹射的时候，越粗糙的表面就损失的能量越多，才会产生这个现象。

因此我们需要把丢失的能量补回去。
(这一段的意思是只保证DFG项正确没用，能量是不守恒的，因此必须要补回去，原因是G项只考虑了一次bounce)

在离线渲染中，我们去考虑了多次bounce，在微表面做一个类似光线追踪的东西，结果准确但速度很慢，更不要提在RTR中了。

但在RTR中有自己的方法去补足丢失的能量。
其核心思路是将反射光看作两种情况：

• 当不被遮挡的时候，这些光就会被看到
• 当反射光被微表面遮挡的时候，认为这些被挡住的光将进行后续的弹射，直到能被看到
  

通过basis idea 从而有了工业界中的处理方法

the Kulla-Conty Approxiamtion

这种方法是通过经验去补全多次反射丢失的能量，其实是创建一个模拟多次反射表面反射的附加BRDF波瓣->fms，利用这个BRDF算出消失的能量作为能量的补偿项（Energy Compensation Term），那么我需要考虑两件事：
1.在反射时有多少能量丢失了？
2.最后反射出的能量有多少？

首先我们先来算最后反射除了多少的能量：
下面的式子是把BRDF（这里的BRDF指的是考虑了Shadowing-Masking的BRDF）、Lighting 、cos在一起在整个半球上进行了积分，来计算射出的总能量

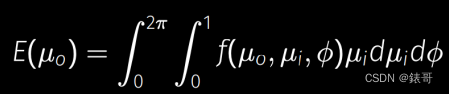
这里非常复杂：

• 我们认为任何方向入射的Radiance是1，也就是rendering equation中的lighting项是1（因为是1，所以式子中没有出现）
• 同样假设BRDF是各项同性的，也就是与i，o无关的
• 因此最终积分的结果意义是，在uniform的lighting=1的情况下，在经历了1 bounce之后射出的总能量E（uo）.

至于cosθ去了哪里？

由于我们积分中是BRDF•cosθ•sinθdθdφ,sinθdΦdφ是单位立体角。
我们将cosθsinθdθdφ放在一起，sinθcosθdθ =sinθd(sinθ)，
所以原式子变成了BRDF•sinθd(sinθ)dφ。
最后我们用u=sinθ进行一个换元操作，得出最后的公式

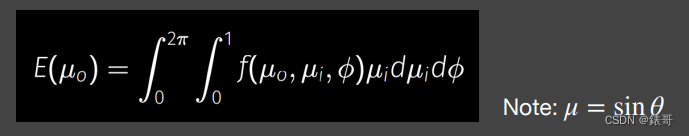
看一下最终详细推导过程（过程中需要进行换元）：

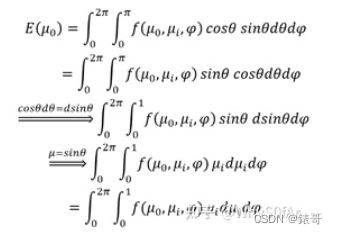
由于得到的射出的总能量E(U0)是在0-1之间的，

• 那么有多少能量被遮挡就是1-E(U0)
• 不同方向积分出来的值是不同的，因此不同观察方向损失的能量1-E(U0)我们可以求出来了，那么只需要加上这一部分能量就解决问题了。
  由于BRDF的可逆性，因此除了考虑o的方向外，还要考虑i的方向（也就是要考虑入射丢失的和出射丢失的），同时要乘一个归一化的量c（可以是常量或函数）得出一个brdf也就是：
  

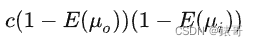
通过这个brdf积分后得到的结果要等于消失的能量->1-E(u0)

之所以这么做是因为简单，我们保留下需要求出来的积分值1-E(u0)，并且考虑由于brdf可逆性的另外半边的1-E(ui)，剩下的部分我们写成一个常数c不去管他，这个C是可以求出来的。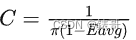

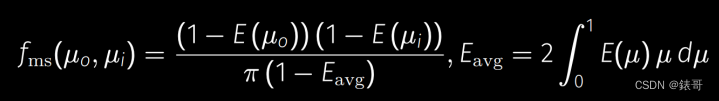
我们代入验证一下变量Ems是否正确

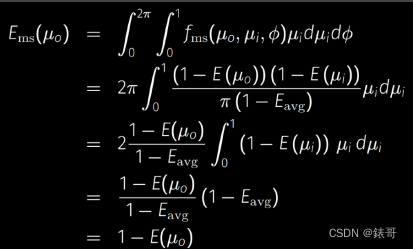
代入后发现求出的E正好是消失的能量

它的原理是希望设计一种可以交换输入输出方向的brdf->fms,使得它的积分结果正是我们所失去的能量,因此用失去的+射出的能量达到能量守恒.

那么到目前为止Eavg的积分如下式

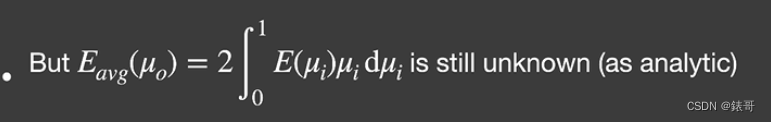
其中E(μ)已经是一个二重积分了，计算是非常困难的，因此计算仍然比较复杂

但是对于一个很复杂的、不一定有解析解的积分可以通过预计算或打表格的方式来解决。

由于考虑到存储的开销,对于这个积分，维度不能太高，这就取决于这个积分依赖的参数，

Eavg经过观察积分式可知不管计算多复杂，Eavg只依赖于μ0与粗糙度,于是我们根据uo和粗糙度打出一张表格:

从而可以很快的知道对应的Eavg的积分值，知道了Eavg的积分值后就可以代入到fms中，从而求出EMS（消失的能量）。

我们将算出的损失的能量加上后可以看到效果很好.

当单次反射的BRDF是有颜色情况怎么办？

• 有颜色就意味着，物体发生了能量吸收的情况，也就是有额外的能量损失，也就是单词反射的积分结果不是1,
• 因此我们可以先考虑没有颜色的情况，然后再去考虑他的颜色是什么

Favg - >平均菲涅尔项：

不管入射角多大，平均每次反射会有多少能量反射

因此平均菲涅尔项的计算就是计算在所有角度下，菲涅尔项的平均值。

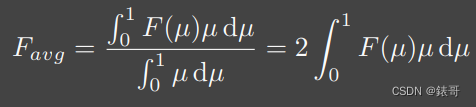
之前的Euo是固定方向上看，整个出去的能量是多少，也就是说这些能量是不会参与到后续多次的反射中的,因此我在后续需要的能参与到后续bounce的是(1-Euo)。

因此我们能看到的能量就能够被分为不同的类型：

能够直接看到的能量：Favg * Euo
一次弹射后能看到的能量Favg * (1-Euo) * FavgEavg
…….
k次反射后能看到的能量Favg ^k* (1-Euo))^k * FavgEavg

那么把0次到k次弹射的结果相加后，能够得到一个无穷级数，最终得到了下式中的颜色项，

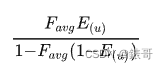
这个颜色项需要直接乘进没有颜色的BRDF->fms中从而得到有颜色的时候除去吸收能量外应该补足的能量.

增加了颜色项后的结果如下图所示。

目前存在的不正确的hack/近似方法：

最近几年有人不考虑能量损失直接加Diffuse项,也就是用一个diffuse+一个Microfacet,这种写法在计算机视觉里尤其常见

这是相当错误的方法，原因：

这是因为已经采用了微表面模型，就不能在与宏观表面模型Diffuse的假设一同采用，同样在物理上也是错误的，能量不能保证守恒，可能会出现发光的BRDF的情况。由于不同角度、不同粗糙度损失的能量是完全不同的，因此直接加一个Diffuse是完全错误的。

总结下来就是：没有物理依据，无法保持能量守恒(宏观概念和微观概念不能混用)。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！