几个有关栈的题目

例题

• 设栈的顺序存储空间为S（1：50），初始状态为top=-1。现经过一系列正常的入栈与退栈操作后，top=30，则当前栈中的元素个数为（　D　）。
  A.20
  B.19
  C.31
  D.30
• 设栈的顺序存储空间为S（1：m），初始状态为top=m+1，则栈中的数据元素个数为（　B　）。
  A.top-m+1
  B.m-top+1
  C.m-top
  D.top-m
• 设栈的顺序存储空间为 S(1:m) ，初始状态为 top=m+1 。现经过一系列正常的入栈与退栈操作后， top=1 ，现又要将一个元素进栈，栈顶指针top值变为（B ）
  A.0
  B.发生栈满的错误
  C.m
  D.2
• 设栈的顺序存储空间为S（1：m），初始状态为top=0。现经过一系列正常的入栈与退栈操作后，top=m+1，则当前栈中的元素个数为（　C　）。
  A.0
  B.m
  C.不可能
  D.m+1
  -设栈的顺序存储空间为 S(1:m) ，初始状态为 top=m+1 。经过一系列入栈与退栈操作后， top=m ，现又在栈中退出一个元素后，栈顶指针top值变为（C ）
  A.0
  B.m-1
  C.m+1
  D.产生栈空错误
• 设栈的顺序存储空间为S（1：50），初始状态为top=51。现经过一系列正常的入栈与退栈操作后，top=20，则当前栈中的元素个数为（　A　）。
  A.31
  B.30
  C.21
  D.20

解析

• 栈相关基础知识：

  1. 栈(stack)是限定仅在表尾进行插入或删除操作的线性表。
  2. 栈又称为后进先出（last in first out）的线性表（简称LIFO结构）。
  3. 对于栈来说，表尾端有其特殊含义，称为栈顶（top），相应的，表头端称为栈底（bottom）。
     

• 题目关键词解释：

  1. 栈的顺序存储空间为S（1：50）/ S（1：m）
     答：这里的（1：50）和（1：m）指的都是栈的空间大小,也就是指能储存多少个数据元素。
  2. 初始状态
     答：栈最初的状态，分为两种栈空和栈中已有数据两种情况（上述例题都为栈空状态，原因见下文详细分析)

• 详细分析：

  1. 栈的存储空间S（1，m），可以理解为一个可以容纳m个数据的空间，本身是看不出方向的，因此要根据数据进出栈是的指针变化来区分正栈和倒栈。
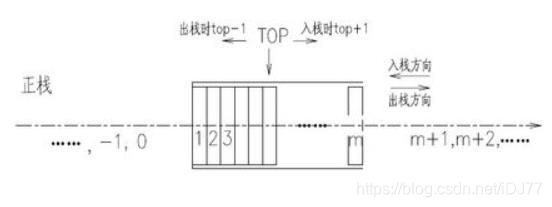
  2. 对于正栈，栈底为1，栈顶可以为1~m之间任何一个数，但是top=m表示栈满，top不可能指向大于m的任何数字，此时，栈中的元素数量等于top-1+1，对于正栈，栈空的时候top可以是0，-1，-2…中的任何一个数，可以理解为每出栈一个数据，栈顶指针top-1，直到top=0，栈已空，此时top虽然可以继续-1但无数据出栈，栈仍是空的。
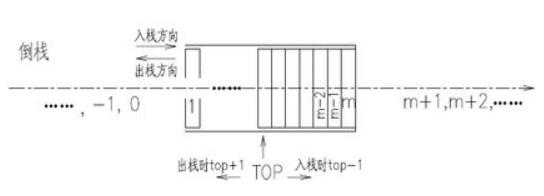
  3. 对于倒栈，栈底为m，栈顶可以为1~m之间任何一个数，但是top=1表示栈满，top不可能指向小于1的任何数字，此时，栈中的元素数量等于m-top+1，对于倒栈，栈空的时候top可以是m+1，m+2，m+3…中的任何一个数，可以理解为每出栈一个数据，栈顶指针top+1，直到top=m+1，栈已空，此时top虽然可以继续+1但无数据出栈，栈仍是空的。
     
  4. 所以根据初始状态栈空时的栈顶指针，可以分析判断是为正栈还是倒栈，再按照相应的栈顶指针变化规律来计算栈中数据的数量。
     初始状态top值有以下三种情况
     - top<1，不在1~m范围，此时栈空，同时也说明top值变化的顺序为由1到m，即为正栈
     - top>m，不在1~m范围，此时栈空，同时也说明top值变化的顺序为由m到1，即为倒栈
     - 1<=top<=m 属于1~m范围，此时栈不为空，无法判断top变化顺序，题目也不会这么出

总结

• 个人觉得吧，正常学数据结构中的栈一般没有分所谓的正/倒，这个分法也是网上看到的，另一种说法好像叫做栈开口向上和开口向下，平时我们所见到的基本都是正栈也就是开口向上，top[-1] (或top[0])表示空，数据入栈时由top[0]（或top[1]）开始，指针不断增大，直到满栈提示。这些例题是二级里面的，反正翻数据结构题没有这种题型，可能是为了出题而出题的吧…

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！