机器学习基础-聚类算法
聚类算法中的数据没有标签
1、K-means算法
1-1、算法步骤
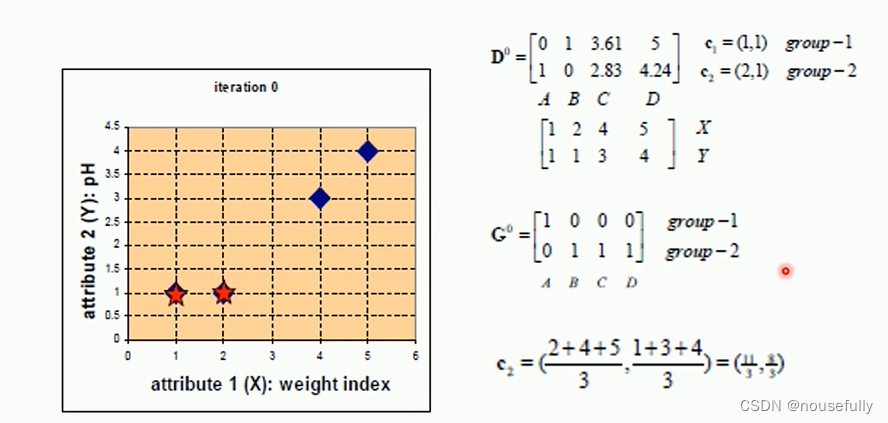
1.先从没有标签的元素集合A中随机取k个元素,作为k个子集各自的重心。
2.分别计算剩下的元素到k个子集重心的距离(这里的距离也可以使用欧氏距离) , 根据距离将这些元素分别划归到最近的子集。
3.根据聚类结果,重新计算重心(重心的计算方法是计算子集中所有元素各个维度的算数平均数)。
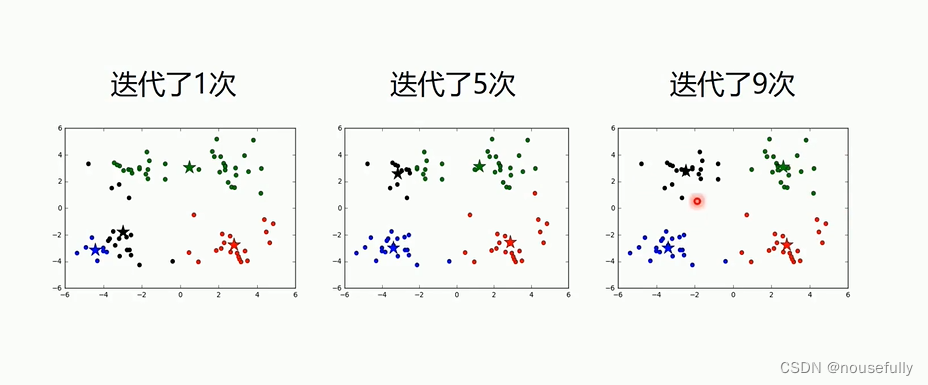
4.将集合A中全部元素按照新的重心然后再重新聚类。
5.重复第4步,直到聚类结果不再发生变化。
1-2、例子


2、实战K-means算法
#%%import numpy as np
import matplotlib.pyplot as plt #%%# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")plt.scatter(data[:,0],data[:,1])
plt.show()#%%data.shape#%% md# 训练模型#%%# 计算距离
def euclDistance(vector1, vector2): return np.sqrt(sum((vector2 - vector1)**2))# 初始化质心
def initCentroids(data, k): numSamples, dim = data.shape #得到行数,列数# k个质心,列数跟样本的列数一样centroids = np.zeros((k, dim))# 随机选出k个质心for i in range(k): # 随机选取一个样本的索引index = int(np.random.uniform(0, numSamples)) # 作为初始化的质心centroids[i, :] = data[index, :] return centroids # 传入数据集和k的值
def kmeans(data, k): # 计算样本个数numSamples = data.shape[0] # 样本的属性,第一列保存该样本属于哪个簇,第二列保存该样本跟它所属簇的误差clusterData = np.array(np.zeros((numSamples, 2))) # 决定质心是否要改变的变量 要改变clusterChanged = True # 初始化质心 centroids = initCentroids(data, k) while clusterChanged: clusterChanged = False # 循环每一个样本 for i in range(numSamples): # 最小距离minDist = 100000.0 # 定义样本所属的簇minIndex = 0 # 循环计算每一个质心与该样本的距离for j in range(k): # 循环每一个质心和样本,计算距离distance = euclDistance(centroids[j, :], data[i, :]) # 如果计算的距离小于最小距离,则更新最小距离if distance < minDist: minDist = distance # 更新最小距离clusterData[i, 1] = minDist# 更新样本所属的簇minIndex = j # 如果样本的所属的簇发生了变化if clusterData[i, 0] != minIndex: # 质心要重新计算clusterChanged = True# 更新样本的簇clusterData[i, 0] = minIndex# 更新质心for j in range(k): # 获取第j个簇所有的样本所在的索引cluster_index = np.nonzero(clusterData[:, 0] == j)# 第j个簇所有的样本点pointsInCluster = data[cluster_index] # 计算质心centroids[j, :] = np.mean(pointsInCluster, axis = 0)
# showCluster(data, k, centroids, clusterData)return centroids, clusterData # 显示结果
def showCluster(data, k, centroids, clusterData): numSamples, dim = data.shape if dim != 2: print("dimension of your data is not 2!") return 1 # 用不同颜色形状来表示各个类别 前面代表形状 后面代表颜色mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark): print("Your k is too large!") return 1 # 画样本点 for i in range(numSamples): markIndex = int(clusterData[i, 0]) plt.plot(data[i, 0], data[i, 1], mark[markIndex]) # 用不同颜色形状来表示各个类别mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', ' 3、实践 sklearn-K-MEANS算法
#%%from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt#%%# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")
# 设置k值
k = 4 #%%# 训练模型
model = KMeans(n_clusters=k)
model.fit(data)#%%# 分类中心点坐标
centers = model.cluster_centers_
print(centers)#%%# 预测结果
result = model.predict(data)
print(result)#%%model.labels_#%%# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):plt.plot(d[0], d[1], mark[result[i]])# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):plt.plot(center[0],center[1], mark[i], markersize=20)plt.show()#%%# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 显示结果
# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):plt.plot(d[0], d[1], mark[result[i]])# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):plt.plot(center[0],center[1], mark[i], markersize=20)plt.show()#%%4、实践sklearn-Mini-Batch-K-MEANS算法
数据量非常大时可以使用该算法
#%%from sklearn.cluster import MiniBatchKMeans
import numpy as np
import matplotlib.pyplot as plt#%%# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")
# 设置k值
k = 4 #%%# 训练模型
model = MiniBatchKMeans(n_clusters=k)
model.fit(data)#%%# 分类中心点坐标
centers = model.cluster_centers_
print(centers)#%%# 预测结果
result = model.predict(data)
print(result)#%%# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):plt.plot(d[0], d[1], mark[result[i]])# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):plt.plot(center[0],center[1], mark[i], markersize=20)plt.show()#%%# 获取数据值所在的范围
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))z = model.predict(np.c_[xx.ravel(), yy.ravel()])# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 显示结果
# 画出各个数据点,用不同颜色表示分类
mark = ['or', 'ob', 'og', 'oy']
for i,d in enumerate(data):plt.plot(d[0], d[1], mark[result[i]])# 画出各个分类的中心点
mark = ['*r', '*b', '*g', '*y']
for i,center in enumerate(centers):plt.plot(center[0],center[1], mark[i], markersize=20)plt.show()#%%5、K-means算法的4个问题
Q1:对k个初始质心的选择比较敏感,容易陷入局部最小值。
例如,我们上面的算法运行的时候,有可能会得到不同的结果,如下面这两种情况。K-means也是收敛了,只是收敛到了局部最小值:
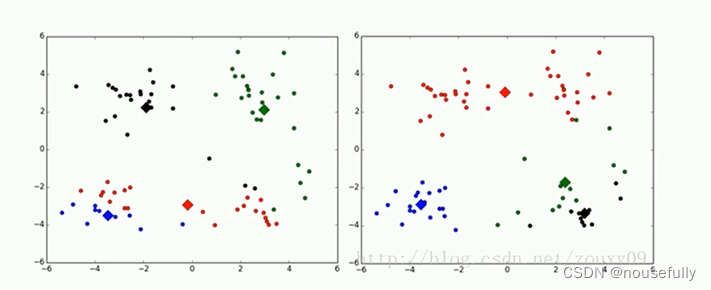
Q2: k值的选择是用户指定的,不同的k得到的结果会有挺大的不同,如下图所示,左边是k=3的结果,蓝色的簇太稀疏了,蓝色的簇应该可以再划分成两个簇。右边是k=5的结果,红色和蓝色的簇应该合并为-一个簇。
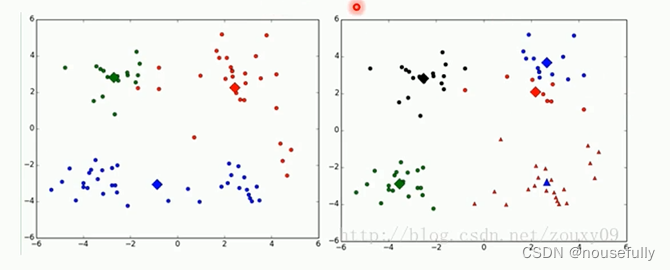
Q3:存在局限性,如下面这种非球状的数据分布就搞不定了: (可以根据密度分类算法)
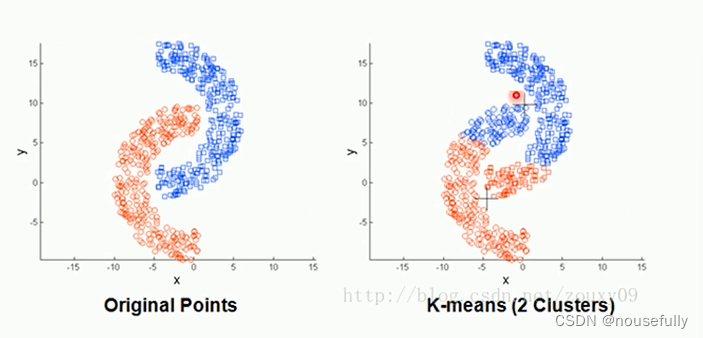
Q4:数据比较大的时候,收敛会比较慢。
6、针对问题1解决方案
使用多次的随机初始化,计算每一次建模得到的代价函数的值,选取代价函数最小结果作为聚类结果。
#%%import numpy as np
import matplotlib.pyplot as plt #%%# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")#%% md# 训练模型#%%# 计算距离
def euclDistance(vector1, vector2): return np.sqrt(sum((vector2 - vector1)**2))# 初始化质心
def initCentroids(data, k): numSamples, dim = data.shape# k个质心,列数跟样本的列数一样centroids = np.zeros((k, dim)) # 随机选出k个质心for i in range(k): # 随机选取一个样本的索引index = int(np.random.uniform(0, numSamples)) # 作为初始化的质心centroids[i, :] = data[index, :] return centroids # 传入数据集和k的值
def kmeans(data, k): # 计算样本个数numSamples = data.shape[0] # 样本的属性,第一列保存该样本属于哪个簇,第二列保存该样本跟它所属簇的误差clusterData = np.array(np.zeros((numSamples, 2))) # 决定质心是否要改变的变量clusterChanged = True # 初始化质心 centroids = initCentroids(data, k) while clusterChanged: clusterChanged = False # 循环每一个样本 for i in range(numSamples): # 最小距离minDist = 100000.0 # 定义样本所属的簇minIndex = 0 # 循环计算每一个质心与该样本的距离for j in range(k): # 循环每一个质心和样本,计算距离distance = euclDistance(centroids[j, :], data[i, :]) # 如果计算的距离小于最小距离,则更新最小距离if distance < minDist: minDist = distance # 更新样本所属的簇minIndex = j # 更新最小距离clusterData[i, 1] = distance# 如果样本的所属的簇发生了变化if clusterData[i, 0] != minIndex: # 质心要重新计算clusterChanged = True# 更新样本的簇clusterData[i, 0] = minIndex# 更新质心for j in range(k): # 获取第j个簇所有的样本所在的索引cluster_index = np.nonzero(clusterData[:, 0] == j)# 第j个簇所有的样本点pointsInCluster = data[cluster_index] # 计算质心centroids[j, :] = np.mean(pointsInCluster, axis = 0)
# showCluster(data, k, centroids, clusterData)return centroids, clusterData # 显示结果
def showCluster(data, k, centroids, clusterData): numSamples, dim = data.shape if dim != 2: print("dimension of your data is not 2!") return 1 # 用不同颜色形状来表示各个类别mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark): print("Your k is too large!") return 1 # 画样本点 for i in range(numSamples): markIndex = int(clusterData[i, 0]) plt.plot(data[i, 0], data[i, 1], mark[markIndex]) # 用不同颜色形状来表示各个类别mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', ' 7、针对问题2解决方案
肘部法则来选择k的值
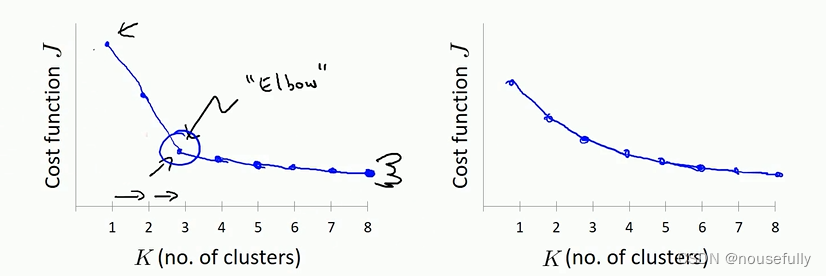
#%%import numpy as np
import matplotlib.pyplot as plt#%%# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")#%% md# 训练模型#%%# 计算距离
def euclDistance(vector1, vector2):return np.sqrt(sum((vector2 - vector1)**2))# 初始化质心
def initCentroids(data, k):numSamples, dim = data.shape# k个质心,列数跟样本的列数一样centroids = np.zeros((k, dim))# 随机选出k个质心for i in range(k):# 随机选取一个样本的索引index = int(np.random.uniform(0, numSamples))# 作为初始化的质心centroids[i, :] = data[index, :]return centroids# 传入数据集和k的值
def kmeans(data, k):# 计算样本个数numSamples = data.shape[0]# 样本的属性,第一列保存该样本属于哪个簇,第二列保存该样本跟它所属簇的误差clusterData = np.array(np.zeros((numSamples, 2)))# 决定质心是否要改变的变量clusterChanged = True# 初始化质心centroids = initCentroids(data, k)while clusterChanged:clusterChanged = False# 循环每一个样本for i in range(numSamples):# 最小距离minDist = 100000.0# 定义样本所属的簇minIndex = 0# 循环计算每一个质心与该样本的距离for j in range(k):# 循环每一个质心和样本,计算距离distance = euclDistance(centroids[j, :], data[i, :])# 如果计算的距离小于最小距离,则更新最小距离if distance < minDist:minDist = distance# 更新样本所属的簇minIndex = j# 更新最小距离clusterData[i, 1] = distance# 如果样本的所属的簇发生了变化if clusterData[i, 0] != minIndex:# 质心要重新计算clusterChanged = True# 更新样本的簇clusterData[i, 0] = minIndex# 更新质心for j in range(k):# 获取第j个簇所有的样本所在的索引cluster_index = np.nonzero(clusterData[:, 0] == j)# 第j个簇所有的样本点pointsInCluster = data[cluster_index]# 计算质心centroids[j, :] = np.mean(pointsInCluster, axis = 0)
# showCluster(data, k, centroids, clusterData)return centroids, clusterData# 显示结果
def showCluster(data, k, centroids, clusterData):numSamples, dim = data.shapeif dim != 2:print("dimension of your data is not 2!")return 1# 用不同颜色形状来表示各个类别mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', ' len(mark):print("Your k is too large!")return 1# 画样本点for i in range(numSamples):markIndex = int(clusterData[i, 0])plt.plot(data[i, 0], data[i, 1], mark[markIndex])# 用不同颜色形状来表示各个类别mark = ['*r', '*b', '*g', '*k', '^b', '+b', 'sb', 'db', ' 8、可视化K-means
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
9、DBSCAN聚类算法
DBSCAN = Density-Based Spatial Clusteringof Applications with Noise
本算法将具有足够高密度的区域划分为簇,并可以发现任何形状的聚类
基于密度的方法,任何形状都适合使用
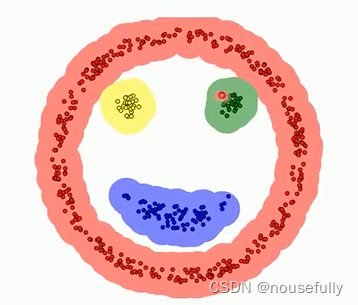

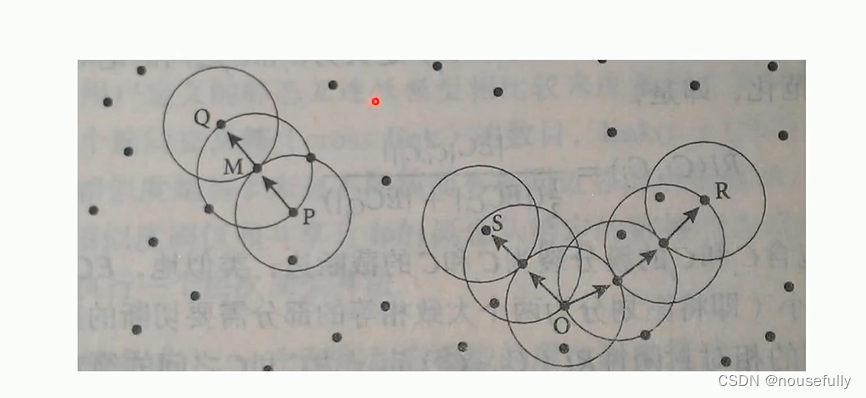
算法思想:
1.指定合适的8和Minpoints。
2.计算所有的样本点,如果点p的e邻域里有超过Minpoints个点,则创建一个以p为核心点的新族。
3.反复寻找这些核心点直接密度可达(之后可能是密度可达)的点,将其加入到相应的簇,对于核心点发生"密度相连”状况的簇,给予合并。
4.当没有新的点可以被添加到任何簇时,算法结束。
算法缺点:

比较:

实践1:
#%%from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt#%%# 载入数据
data = np.genfromtxt("kmeans.txt", delimiter=" ")#%%# 训练模型
# eps距离阈值,min_samples核心对象在eps领域的样本数阈值
model = DBSCAN(eps=2, min_samples=4)
model.fit(data)#%%result = model.fit_predict(data)
result#%%# 画出各个数据点,用不同颜色表示分类 6个结果 -1属于噪声
mark = ['or', 'ob', 'og', 'oy', 'ok', 'om']
for i,d in enumerate(data):plt.plot(d[0], d[1], mark[result[i]])plt.show()#%%
实践2:
#%%import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets#%%x1, y1 = datasets.make_circles(n_samples=2000, factor=0.5, noise=0.05)
x2, y2 = datasets.make_blobs(n_samples=1000, centers=[[1.2,1.2]], cluster_std=[[.1]])x = np.concatenate((x1, x2))
plt.scatter(x[:, 0], x[:, 1], marker='o')
plt.show()#%%from sklearn.cluster import KMeans
y_pred = KMeans(n_clusters=3).fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()#%%from sklearn.cluster import DBSCAN
y_pred = DBSCAN().fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()#%%y_pred = DBSCAN(eps = 0.2).fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()#%%y_pred = DBSCAN(eps = 0.2, min_samples=50).fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()#%%
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!