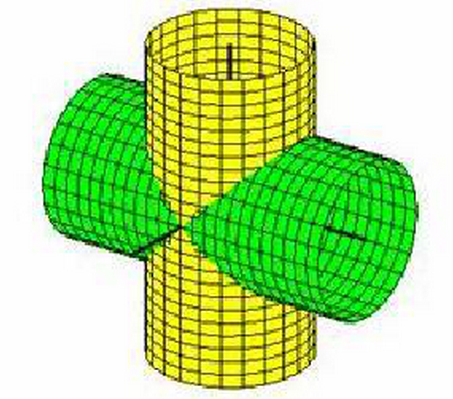
二重积分-两个直交圆柱面所围成的立体理解
参考博客:http://t.csdn.cn/yXvFV
目录
解决问题:理解两个直交圆柱面所围成的立体其确立方式
几何直观理解:
相关例题:
“小刀牛试”:
解决问题:理解两个直交圆柱面所围成的立体其确立方式
几何直观理解:
确定所围立体图形外围形状:(确定了外围形状实心立体几何就确定了)
①建立坐标系
②几何对称性研究第一卦限
③确定相交点→点平行确定相交线→线围成相交面
(1,2,3代表确定顺序)
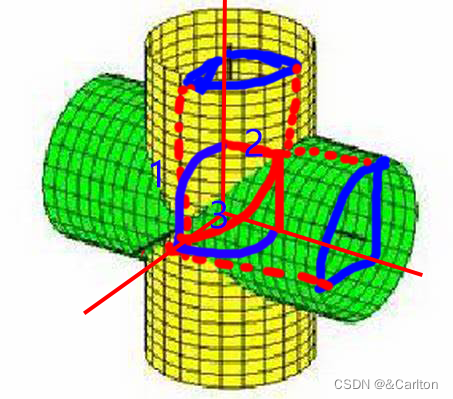
难点:曲线3的确定方法
用坐标一 一 对应的特性,取多个特殊点,集合成线(好像不是这样想,应该是实际上就是长这样所以长成这样)

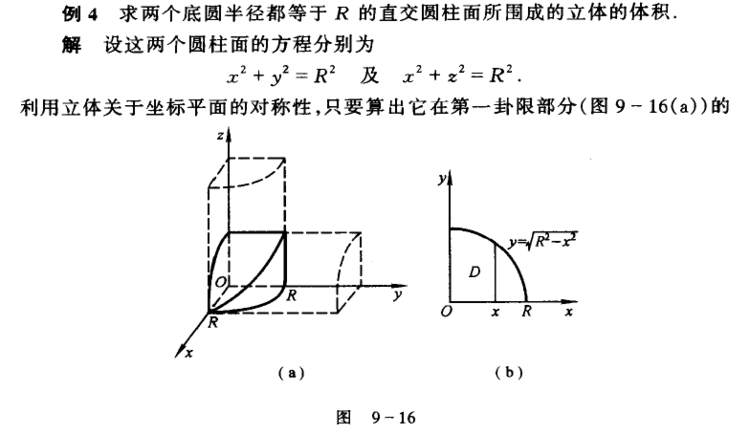
相关例题:
(同济数学第七版下册146页例题)
体积计算方式:
第一卦限部分看成曲顶柱体,拆分研究其底面与顶(降维分析,三维→二维),用二重积分求解。
结果:
“小刀牛试”:
计算维维安尼体积
球面x²+y²+z²=a²与圆柱面x²+y²-ax=0的交线所围成的立体体积
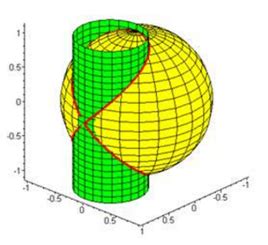
结果:
写在最后:
笔者高数水平有限,仍需继续学习,欢迎有更好思考方式的朋友分享。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!