python拟合反比例函数_基于梯度下降算法的线性回归拟合（附python/matlab/julia代码）...

梯度下降

梯度下降法的原理

梯度下降法(gradient descent)是一种常用的一阶(first-order)优化方法，是求解无约束优化问题最简单、最经典的方法之一。

梯度下降最典型的例子就是从山上往下走，每次都寻找当前位置最陡峭的方向小碎步往下走，最终就会到达山下(暂不考虑有山谷的情况)。

首先来解释什么是梯度？这就要先讲微分。对于微分，相信大家都不陌生，看几个例子就更加熟悉了。

先来看单变量的微分：

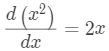
再看多变量的微分：

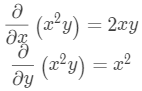
补充:导数和微分的区别

导数是函数在某一点处的斜率，是Δy和Δx的比值；而微分是指函数在某一点处的切线在横坐标取得增量Δx以后，纵坐标取得的增量，一般表示为dy。

梯度就是由微分结果组成的向量，令

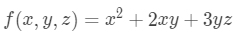
有

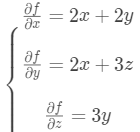
那么，函数f(x,y,z)在(1,2,3)处的微分为

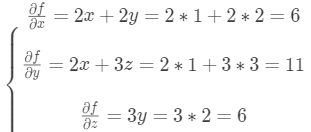
因此，函数f(x,y,z)在(1,2,3)处的梯度为(6,11,6)。

梯度是一个向量，对于一元函数，梯度就是该点处的导数，表示切线的斜率。对于多元函数，梯度的方向就是函数在该点上升最快的方向。

梯度下降法就是每次都寻找梯度的反方向，这样就能到达局部的最低点。

那为什么按照梯度的反方向能到达局部的最低点呢？这个问题直观上很容易看出来，但严禁起见，我们还是给出数学证明。

对于连续可微函数f(x)，从某个随机点出发，想找到局部最低点，可以通过构造一个序列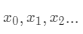,能够满足

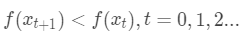
那么我们就能够不断执行该过程即可收敛到局部极小点，可参考下图。

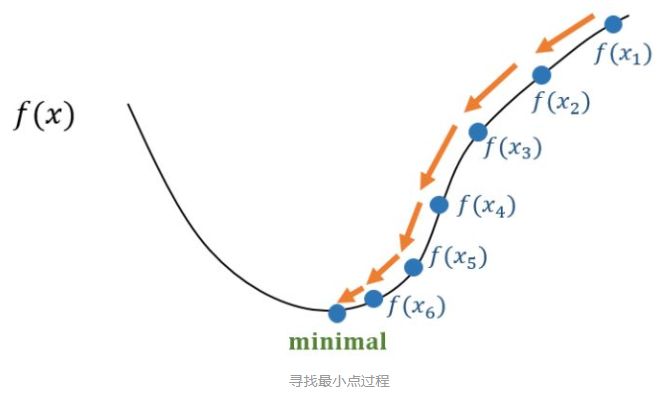
那么问题就是如何找到下一个点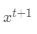 ,并保证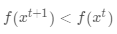呢？我们以一元函数为例来说明。对于一元函数来说，x是会存在两个方向：要么是正方向( 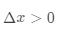)，要么是负方向( 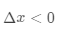)，如何选择每一步的方向，就需要用到大名鼎鼎的泰勒公式，先看一下下面这个泰勒展式：

其中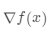表示f(x)在x处的导数。

若想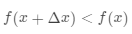,就需要保证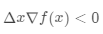，令

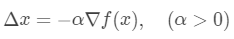
步长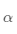是一个较小的正数，从而有

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！