斐波那契数列之差分方程求解

关于斐波那契数列（Fibonacci sequence）之差分方程求解算法一点点记录！

斐波那契数列，又称之为黄金分割数列。具体指的是这样的一个数列：

​ 利用小学数学就能演算出后面的项数，可以很清楚的得到数列的后一项的数值可以由其前面两项的到的。不过得注意的是最初的两项是第0个和第1个数值是分别是0和1，这样不难想到，肯定必须确定前面2项才能确定第三项的值，才能依次确定后面几项，具体规律可以用下面的这个通项式子表示

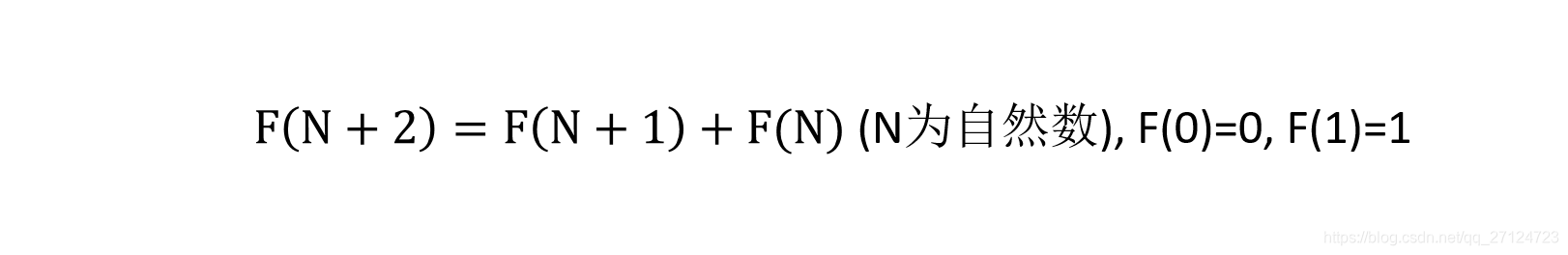
如果直接用递归的思想，估计很快就能写出来这个计数方法。这里我选用python做，工具嘛，哪个方便用哪个。

def Fibonacci(N):if(N<2):return Nelse:return Fibonacci(N-1)+ Fibonacci(N-2)if __name__ == '__main__':with open("Fibonacci.txt","w") as f:for i in range(20):print(Fibonacci(i),end=" ")f.write(str(Fibonacci(i))+"  ")f.close()

python Fibonacci.py 之后就会产生一个文件Fibonacci.txt里面内容如下：

这样迭代对于这样20数据来讲本来就没有压力。我简单测试一哈关于20,25,30,35,40次迭代完成，我电脑需要多少时间。

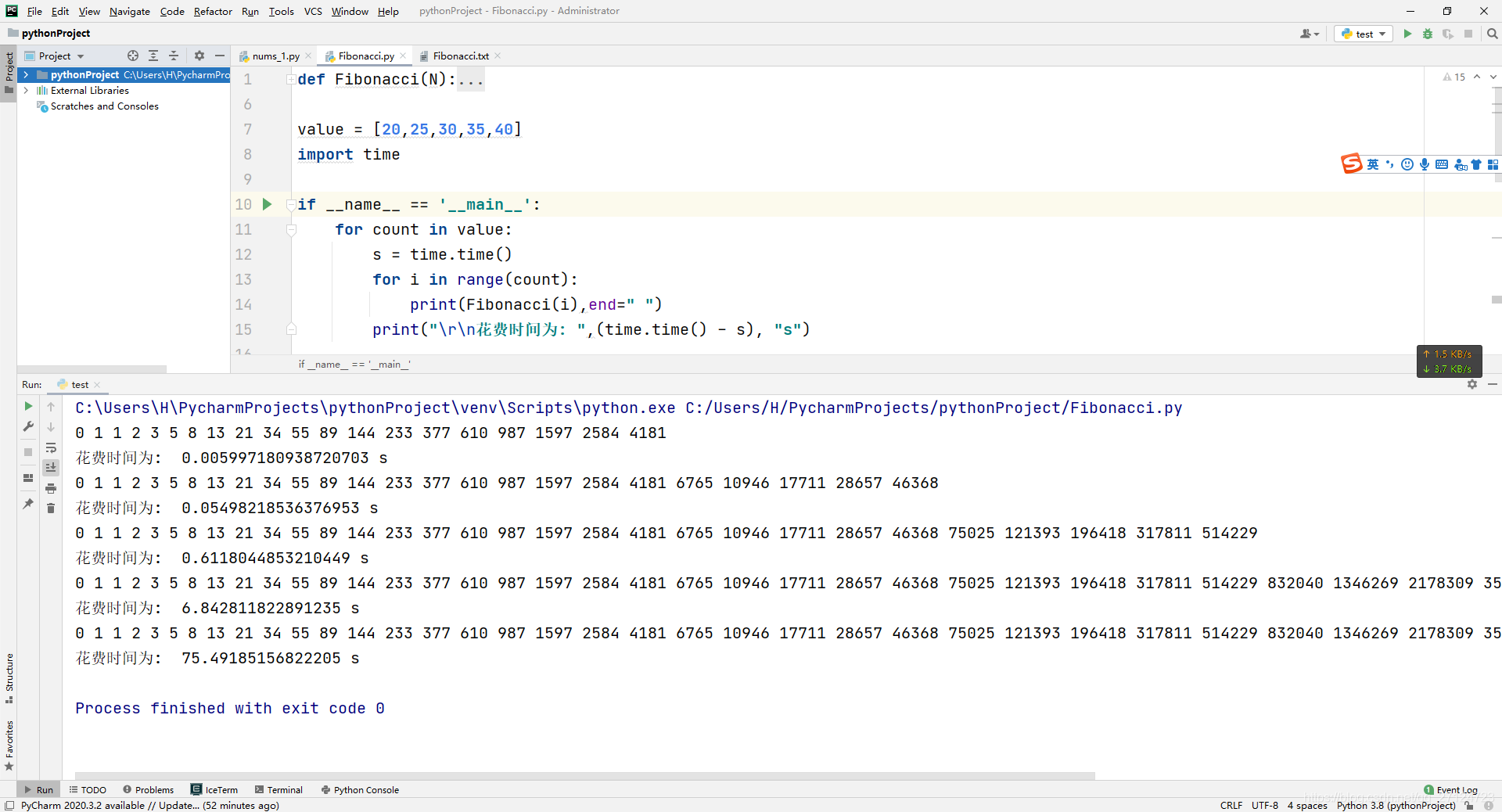
要是迭代100次的话，电脑不疯，我都要疯了，经过测试迭代40次左右的时间，我的台式电脑大致需要1分钟15秒左右。实在不敢测试100次的结果。

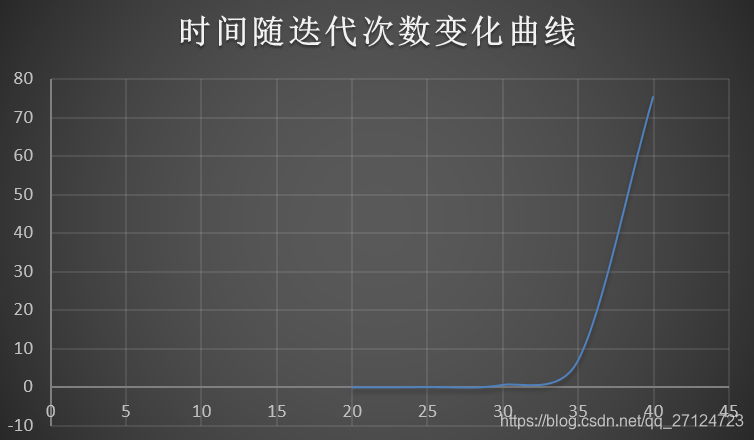
def Fibonacci(N):if(N<2):return Nelse:return Fibonacci(N-1)+ Fibonacci(N-2)
value = [20,25,30,35,40]
import time
if __name__ == '__main__':for count in value:s = time.time()for i in range(count):print(Fibonacci(i),end=" ")print("\r\n花费时间为: ",(time.time() - s), "s")

如何提高这个运算效率呢？？？

解决的办法还是得落在这个表达式里面

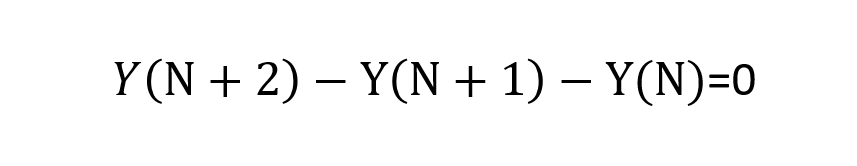
这个形式就是差分方程的形式，我记得这是考研的数三的考点，奈何我考的是数一，不过学过微分方程，大致看了一哈，带公式计算即可，没有太复杂的东西。首先这个表达式是二阶常系数齐次线性差分方程。所谓二阶指的是该差分方程的最高阶数有表达式可以得出，所谓常系数指的是F(N+t) （t为任意自然数）前面的系数为常数，齐次指的是该方程右边为0。

斐波那契数列之差分方程求解过程

利用这个最后的表达式很快敲出代码：

def Fibonacci(N):if(N<2):return Nelse:return Fibonacci(N-1)+ Fibonacci(N-2)def Fibonacci2(N):sqrt5 = 5**0.5fibnN = ((1+sqrt5)/2)**N-((1-sqrt5)/2)**Nreturn round(fibnN/sqrt5)value = [20,25,30,35,40]
import timeif __name__ == '__main__':for count in value:s = time.time()for i in range(count):print(Fibonacci2(i),end=" ")print("\r\n花费时间为: ",(time.time() - s), "s")"""
使用Fibonacci函数
输出:
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 
花费时间为:  0.004997968673706055 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 
花费时间为:  0.056983232498168945 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 
花费时间为:  0.6223404407501221 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 
花费时间为:  6.873619079589844 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 39088169 63245986 
花费时间为:  75.94436860084534 s
""""""
使用Fibonacci2函数
输出:
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
花费时间为:  0.0 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 
花费时间为:  0.0 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 
花费时间为:  0.0 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 
花费时间为:  0.0 s
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946 17711 28657 46368 75025 121393 196418 317811 514229 832040 1346269 2178309 3524578 5702887 9227465 14930352 24157817 39088169 63245986 
花费时间为:  0.00099945068359375 s"""

尝试计算迭代100次，发现Fibonacci2算法仍旧快速输出结果。学好高数，真是能快速解决问题。不知道迭代次数足够多，是否有错误，没有验证过，但是计算是真的快啊

每天学习亿点点，每天进步亿点点！（仅仅是记录自己的学习）要是有错误、或者其他简洁记得请指出来哈！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！