算法设计与分析 实验四 贪心算法

目录

• • 实例1 最优装载问题
  • 实例2 单源最短路径问题
  • 实例3 最小生成树
  • • Prim算法
    • krustal算法

实例1 最优装载问题

问题描述：有一批集装箱要装上一艘载重量为C的轮船。其中集装箱i的重量为Wi。最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船。
问题可以描述为：

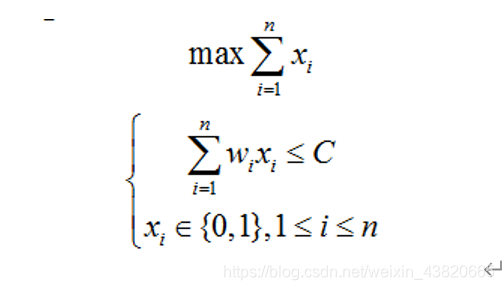
其中，变量xi=0表示不装入集装箱i，xi=1表示装入集装箱i。

问题：采用贪心算法实现最优装载。

//
// Created by 拔牙不打麻药 on 2021/5/17.
//#include "stdio.h"int main(){int i =0;int a[50] = {0};int b[50] = {0};int total_weight = 0;scanf("%d",&total_weight);while (scanf("%d",&a[i])){ //这里终止输入可以用字母i++;}for(int j= 0;j < i; j++){ //冒泡排序将货物从大到小排列for(int k = 0;k < j-1;k++){if(a[k]>a[k+1]){int temp = 0;temp = a[k+1];a[k+1] = a[k];a[k] = temp;}}}for(int j = 0;j < i; j++){ //贪心算法求能放最多的情况if(a[j] < total_weight){total_weight = total_weight - a[j];b[j] = 1;}}printf("被带上船的货物有：\n");for(int j = 0;j < i; j++){if(b[j] != 0){printf("%d,",j+1);}}
}

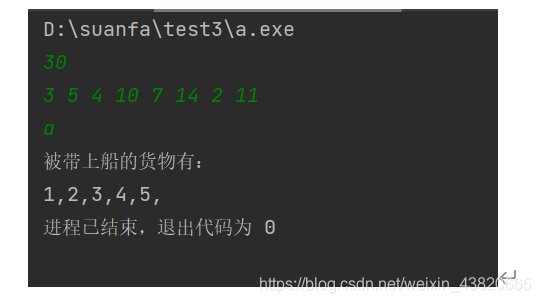
实例2 单源最短路径问题

问题描述：给定带权有向图G =(V,E)，其中每条边的权是非负实数。另外，还给定V中的一个顶点，称为源。现在要计算从源到所有其它各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
问题：实现Dijkstra算法是解单源最短路径问题的贪心算法。
我们用一个例子来具体说明迪杰斯特拉算法的流程。

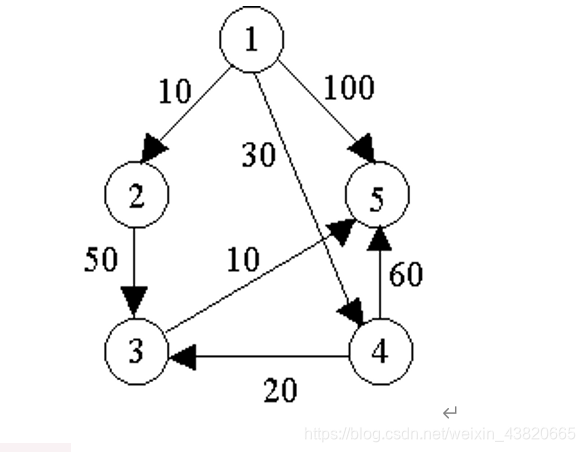
定义源点为0，dist[i]为源点0到顶点i的最短路径。其过程描述如下：

//
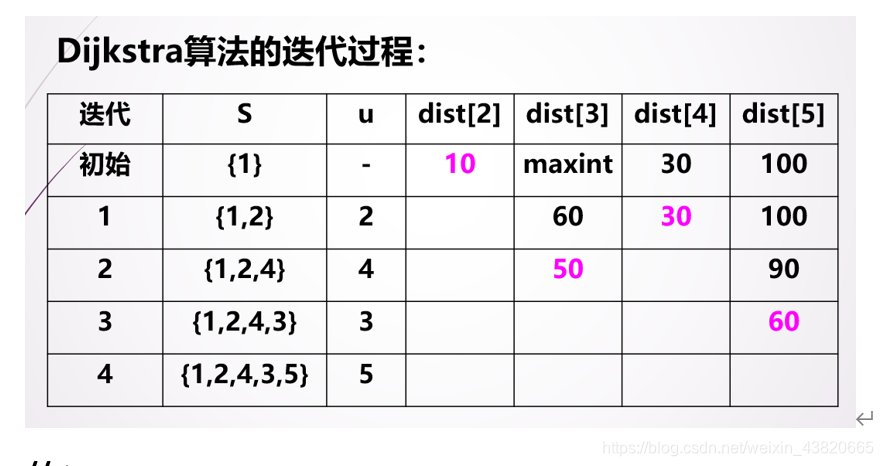
// Created by 拔牙不打麻药 on 2021/5/19.
//#include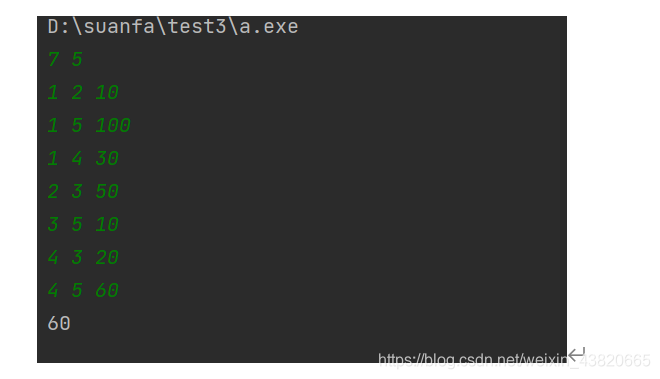
#include
#include
#include
#define Inf 0x3f3f3f3fusing namespace std;int map[500][500];int vis[1000],dis[1000];
int n,m;//n个点，m条边void Init ()
{memset(map,Inf,sizeof(map));for(int i=1;i<=n;i++){map[i][i]=0;}
}void Getmap()
{int u,v,w;for(int t=1;t<=m;t++){scanf("%d %d %d",&u,&v,&w);//输入节点和节点之间的权重if(map[u][v]>w){map[u][v]=w;map[v][u]=w;}}}void Dijkstra(int u)
{memset(vis,0,sizeof(vis));for(int t=1;t<=n;t++){dis[t]=map[u][t];}vis[u]=1;for(int t=1;t<n;t++){int minn=Inf,temp;for(int i=1;i<=n;i++){if(!vis[i]&&dis[i]<minn){minn=dis[i];temp=i;}}vis[temp]=1;for(int i=1;i<=n;i++){if(map[temp][i]+dis[temp]<dis[i]){dis[i]=map[temp][i]+dis[temp];}}}}int main()
{scanf("%d %d",&m,&n);//n个点，m条边Init();Getmap();Dijkstra(n);printf("%d\n",dis[1]);return 0;
}

实例3 最小生成树

问题描述：设G =(V,E)是无向连通带权图，即一个网络。E中每条边(v,w)的权为c[v][w]。如果G的子图G’是一棵包含G的所有顶点的树，则称G’为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中，耗费最小的生成树称为G的最小生成树。

问题：用贪心算法设计策略可以设计出构造最小生成树的有效算法。采用Prim算法和Kruskal算法分别进行实现。

Prim算法

//贪心算法 最小生成树 Prim算法
#include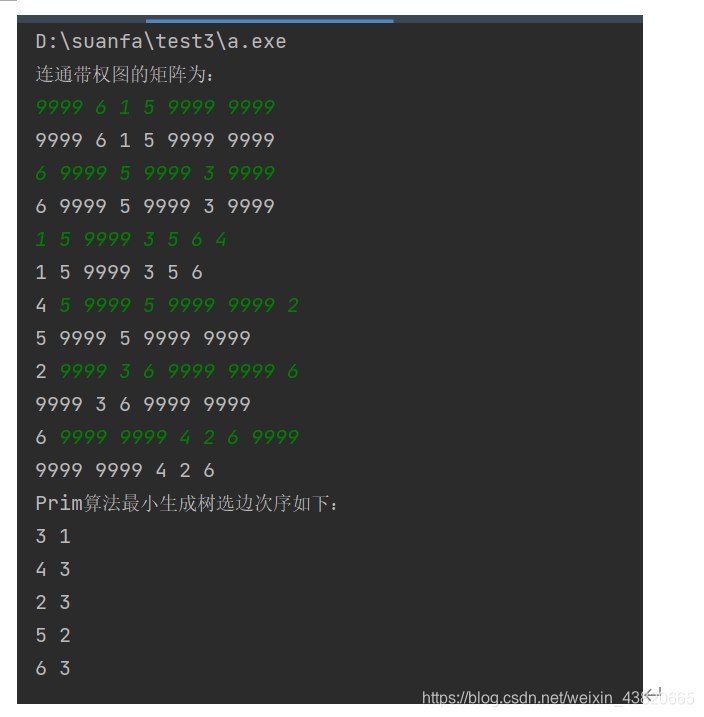 
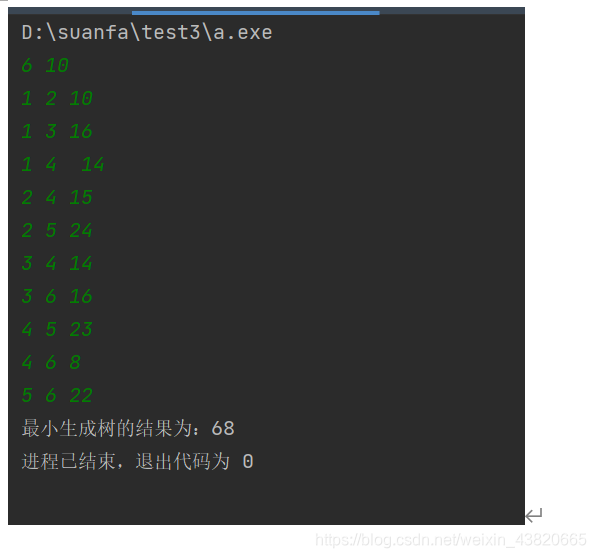
#include 
#include 
using namespace std;#define inf 9999;
const int N = 6;template<class Type>
void Prim(int n,Type c[][N+1]);int main()
{int c[N+1][N+1];cout<<"连通带权图的矩阵为："<<endl;for(int i=1; i<=N; i++){for(int j=1; j<=N; j++){cin>>c[i][j];cout<<c[i][j]<<" ";}cout<<endl;}cout<<"Prim算法最小生成树选边次序如下："<<endl;Prim(N,c);return 0;
}template<class Type>
void Prim(int n,Type c[][N+1])
{Type lowcost[N+1];//记录c[j][closest]的最小权值int closest[N+1];//V-S中点j在S中的最邻接顶点bool s[N+1];s[1] = true;//初始化s[i],lowcost[i],closest[i]for(int i=2; i<=n; i++){lowcost[i] = c[1][i];closest[i] = 1;s[i] = false;}for(int i=1; i<n; i++){Type min = inf;int j = 1;for(int k=2; k<=n; k++)//找出V-S中使lowcost最小的顶点j{if((lowcost[k]<min)&&(!s[k])){min = lowcost[k];j = k;}}cout<<j<<' '<<closest[j]<<endl;s[j] = true;//将j添加到S中for(int k=2; k<=n; k++)//将j添加到S中后，修改closest和lowcost的值{if((c[j][k]<lowcost[k] && (!s[k]))){lowcost[k] = c[j][k];closest[k] = j;}}}
}

krustal算法

参考教程：https://blog.csdn.net/qq_41754350/article/details/81460643

//
// Created by 拔牙不打麻药 on 2021/5/24.
//# include "iostream"
# include "cstdio"
# include "algorithm"
using namespace  std;
int n,m,num = 0,k = 0;
int fat[1000];
struct node{int from,to,distance;
}edge[1000];bool cmp(const node &a,const node &b){return a.distance<b.distance;
}int father(int x){if(fat[x] != x){return father(fat[x]);}elsereturn x;
}void unionn(int x,int y){fat[father(y)] = father(x);
}int main(){scanf("%d %d",&n,&m);//输入点数和边数for (int i = 1; i <= m; i++){scanf("%d %d %d",&edge[i].from,&edge[i].to,&edge[i].distance);//输入每条边的端点和权值}for(int i =1;i <= n; i++){fat[i] = i;}sort(edge+1,edge+m+1, cmp);for (int i = 1; i <= m; i++) {if(k == n-1) break;if(father(edge[i].from) != father(edge[i].to)){unionn(edge[i].from,edge[i].to);num += edge[i].distance;k++;}}printf("最小生成树的结果为：%d",num);return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！