算法2:二分及例题解析
有单调性的一定能二分,但能二分的不一定有单调性。
目录
一、算法解释
二、整数二分
三、整数二分例题示例
数的范围
四、实数二分
五、实数二分例题示例
数的三次方根
六、代码模板及使用条件
七、精选习题
机器人跳跃问题
四平方和
分巧克力(经典思路)
一、算法解释
二分查找也常被称为二分法或者折半查找,每次查找时通过将待查找区间分成两部分并只取一部分继续查找,将查找的复杂度大大减少。对于一个长度为 O(n)的数组,二分查找的时间复杂度为 O(log n)。
举例来说,给定一个排好序的数组(3,4,5,6,7),我们希望查找4在不在这个数组内。第一次折半时考虑中位数5,因为5大于4,所以如果4存在于这个数组,那么其必定存在于5左边这一半。于是我们的查找区间变成了(3,4,5) (注意,根据具体情况和您的刷题习惯,这里的5可以保留也可以不保留,并不影响时间复杂度的级别)。第二次折半时考虑新的中位数 4,正好是我们需要查找的数字。于是我们发现,对于一个长度为5的数组,我们只进行了2次查找。如果是遍历数组,最坏的情况则需要查找5次。
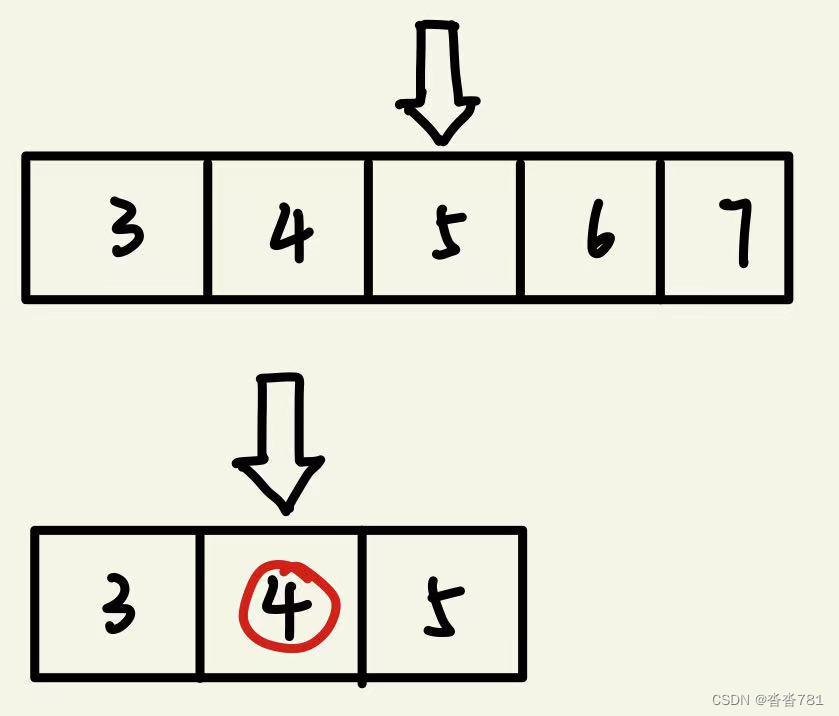
具体到代码上,二分查找时区间的左右端取开区间还是闭区间在绝大多数时候都可以,因此有些初学者会容易搞不清楚如何定义区间开闭性。这里我提供两个小诀窍,第一是尝试熟练使用一种写法,比如左闭右开(满足 C++、Python 等语言的习惯)或左闭右闭(便于处理边界条件),尽量只保持这一种写法;第二是在刷题时思考如果最后区间只剩下一个数或者两个数,自己的写法是否会陷人死循环,如果某种写法无法跳出死循环,则考虑尝试另一种写法。
二分查找也可以看作双指针的一种特殊情况,但我们一般会将二者区分。双指针类型的题,指针通常是一步一步移动的,而在二分查找里,指针每次移动半个区间长度。
二、整数二分
整数二分步骤:
①确定一个区间,使得目标值在一定区间内
②想一个性质,满足两点:一是该性质具有二段性,即一段满足,另一段不满足,中间没有缺失; 二是该性质下,大部分的答案是分界点(如下述)。
③分析中点M在该判断条件下是否成立,如果成立,考虑答案在哪个区间;如果不成立,考虑答案在哪个区间
④如果更新方式为R=M,则不用做任何处理;如果更新方式为L=M,则需要在计算M时加1。
具体还看下述:
整数的特点就是 数据是离散的,所以答案分为两种情况:左半段终点,或者是右半段起点。
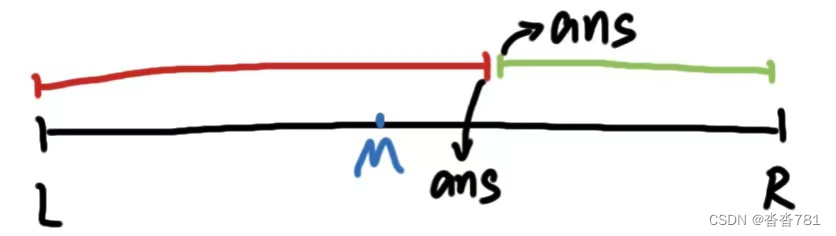
第一类:答案在左半段终点

第二类:答案在右半段起点

(M是否加1,主要看是L=M还是R=M)
三、整数二分例题示例
数的范围
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询 (查询该数在第几个位置)。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0 开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1解析:
该题采用右半段起点
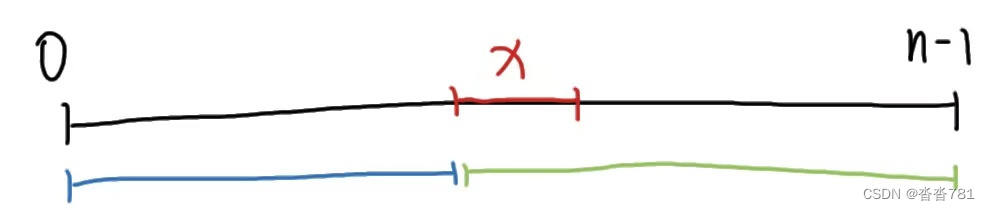
①确定区间:[0,n-1]
②找x使其分成两段:大于等于x的一段和小于x的一段 (x即为要查询的数)
③判断一下是否无解
#include
#include
#include
using namespace std;const int N=100010;int n,m;
int q[N];int main()
{cin>>n>>m; //输入数组长度和询问个数for(int i=0;i>q[i]; //输入完整数组for(int i=0;i>x;//二分x的左端点int l=0,r=n-1; //确定区间范围while(l=x) r=mid;else l=mid+1;}//判断是否有解if(q[r]==x){cout< 四、实数二分
由于实数具有连续性,在找中点时不用考虑加1的问题,所以相对于整数二分来说会比较简单;
但方法步骤与整数二分类似。
实数二分步骤:
①确定一个区间,使得目标值在一定区间内
②将区间[L,R]划分成[L,M],[M,R],判断答案在中点M的哪一边
③什么时候停止二分:当区间足够小的时候 while(R-L>1e-6)

五、实数二分例题示例
数的三次方根
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00
输出样例:
10.000000解析:
①确定区间范围:[-10000,10000]
②找x使其分成两段:M*M*M大于等于x的为一段,小于的为一段
#include
#include
#include
using namespace std;int main()
{double x; //x为输入的浮点数cin>>x;double l=-10000,r=10000;while(r-l>1e-8){double M=(l+r)/2; //M为输出结果,也是中值if(M*M*M >= x) r=M; //数据过大应在前半段 else l=M; //数据过小应在后半段}cout< 六、代码模板及使用条件
使用条件:
一般遇到“最少”“最多”的问题,都要想一下是否可以用二分,然后再依次想能否用DFS, DP, 贪心。
二分大都具有单调性,二段性。
整数二分
bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid; // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}浮点数二分
bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}七、精选习题
机器人跳跃问题
机器人正在玩一个古老的基于 DOS 的游戏。
游戏中有 N+1 座建筑——从 0 到 N 编号,从左到右排列。
编号为 0 的建筑高度为 0 个单位,编号为 i 的建筑高度为 H(i) 个单位。
起初,机器人在编号为 0 的建筑处。
每一步,它跳到下一个(右边)建筑。
假设机器人在第 k 个建筑,且它现在的能量值是 E,下一步它将跳到第 k+1 个建筑。
如果 H(k+1)>E,那么机器人就失去 H(k+1)−E 的能量值,否则它将得到 E−H(k+1) 的能量值。
游戏目标是到达第 N 个建筑,在这个过程中能量值不能为负数个单位。
现在的问题是机器人至少以多少能量值开始游戏,才可以保证成功完成游戏?
输入格式
第一行输入整数 N。
第二行是 N 个空格分隔的整数,H(1),H(2),…,H(N)代表建筑物的高度。
输出格式
输出一个整数,表示所需的最少单位的初始能量值上取整后的结果。
数据范围
1≤N, H(i)≤10的5次方
输入样例1:
5
3 4 3 2 4
输出样例1:
4
输入样例2:
3
4 4 4
输出样例2:
4
输入样例3:
3
1 6 4
输出样例3:
3解析:
题目解释:从低往高跳,能量减少;从高往低跳,能量增加。
如何确定是否有单调性:如果初始值为E0可以满足,大于E0也一定可以满足,就说具有单调性。
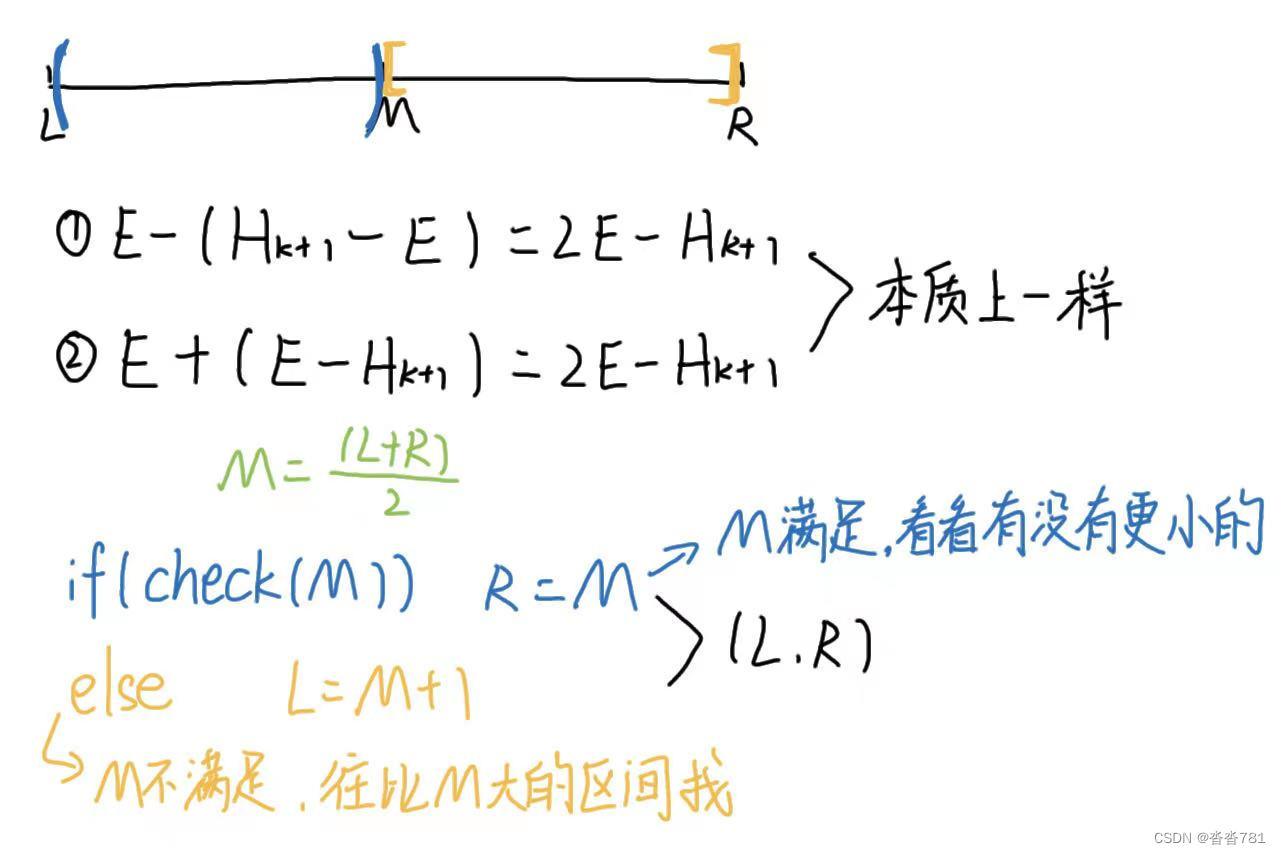
由于E每次都要×2,为防止int爆掉:
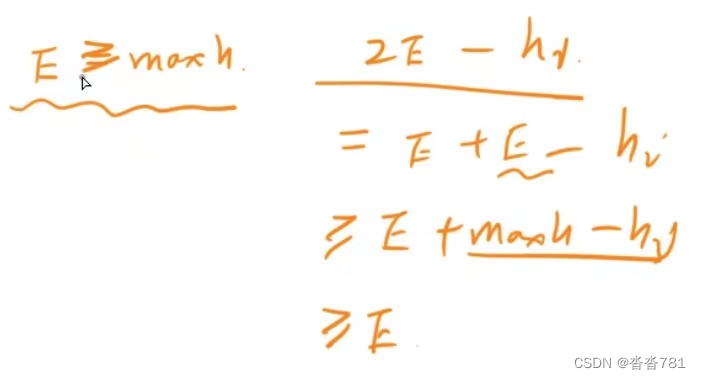
#include
#include
#include
using namespace std;const int N=100010;int n; //建筑数
int h[N]; //建筑高度bool check(int e)
{for(int i=1; i<=n; i++){e=e*2-h[i];if(e>=100000) return true;if(e<0) return false;}return true;}int main()
{cin>>n;for(int i=0;i<=n;i++) cin>>h[i];int l=0,r=100000;while(l 四平方和
四平方和定理,又称为拉格朗日定理:
每个正整数都可以表示为至多 4 个正整数的平方和。
如果把 0 包括进去,就正好可以表示为 4 个数的平方和。
比如:5=0²+0²+1²+2²
对于一个给定的正整数,可能存在多种平方和的表示法。
要求你对 4个数排序:0≤a≤b≤c≤d
并对所有的可能表示法按 a,b,c,d为联合主键升序排列,最后输出第一个表示法。
(即输出字典序最小的一个)
输入格式
输入一个正整数 N。
输出格式
输出4个非负整数,按从小到大排序,中间用空格分开。
数据范围
0 输入样例: 输出样例: 解析: 难点:如何找到字典序最小的解。 解法1:二分 解法2:暴力三重循环 儿童节那天有 K 位小朋友到小明家做客。 小明拿出了珍藏的巧克力招待小朋友们。 小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。 为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。 切出的巧克力需要满足: 例如一块 6×5的巧克力可以切出 6 块 2×2 的巧克力或者 2 块 3×3 的巧克力。 当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么? 输入格式 第一行包含两个整数 N 和 K。 以下 N 行每行包含两个整数 Hi 和 Wi。 (输入保证每位小朋友至少能获得一块 1×1的巧克力) 输出格式 输出切出的正方形巧克力最大可能的边长。 数据范围 1≤N, K≤10的5次方 输入样例: 输出样例: 解析: 边长越大,能切出来的块数就越小 找到一个切出来的边长值,使得块数大于等于小朋友的个数K 的 最大的一个点 结合二分:若答案为X0,<=X0和>X0 即为两部分;性质即是 f(x)>=K5
0 0 1 2#include#include分巧克力(经典思路)
1≤Hi, Wi≤10的5次方2 10
6 5
5 6
2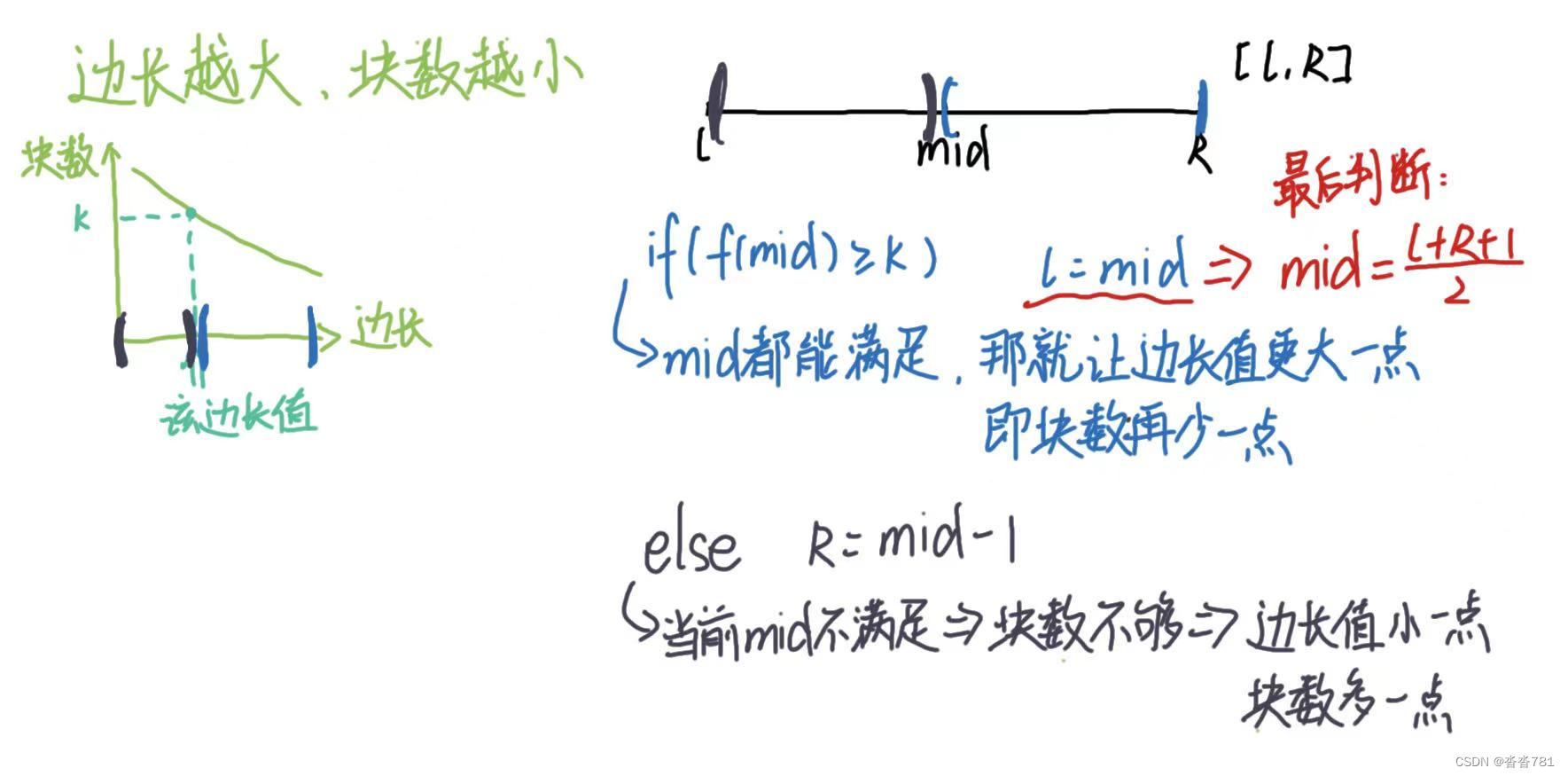
#include
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!