数学建模:模糊数学基础
数学建模:模糊聚类(一)
文章目录
- 数学建模:模糊聚类(一)
- 1.模糊概念
- 1.1模糊子集
- 1.2.模糊概念
- 1.2.1 特征函数的缺点
- 1.2.2 隶属度函数
- 1.3 模糊集的运算
- 1.4 λ \lambda λ截集
- 2.模糊关系
- 2.1经典二元关系
- 2.2 模糊关系
- 2.2.1模糊关系的运算
- 2.2.2模糊关系的合成
- 2.2.3 模糊关系的特性
- 2.2.3模糊等价关系和经典等价关系的联系
- 3.模糊聚类
- 3.1模糊相似关系
- 3.2模糊聚类的关键
- 3.2.1 数据标准化
- 3.3 模糊聚类方法及步骤
- Step1:数据预处理:标准化
- ①平移-标准差变换
- ②平移-极差变换
- Step2:建立模糊相似矩阵
- Step3:聚类
- (1)传递闭包法
- 3.4应用案例(作业)
1.模糊概念
精确概念:时间、地点、男人
模糊概念:大胡子、高个子、长头发、宽边眼镜、中年人
1.1模糊子集
精确概念的数学模型:用论域的经典子集刻画。
经典子集合范围边界分明,即:一个元素x要么属于集合A(记作x∈A),要么不属于集合(记作x∉A),二者必居其一。
已知: U = { x 1 , x 2 , x 3 . . . x n } , A = { x 1 , x 2 , x 5 } U = \{x_1,x_2,x_3...x_n\},A = \{x_1,x_2,x_5\} U={x1,x2,x3...xn},A={x1,x2,x5},定义A的特征函数是满足:
∀ x i ∈ U , C A ( x i ) = { 1 , x i ∈ A 0 , x i ∉ A \forall x_i ∈ U,C_A(x_i) = \begin{cases}1,x_i∈A\\0, x_i∉A \end{cases} ∀xi∈U,CA(xi)={1,xi∈A0,xi∈/A
这样的映射就是:
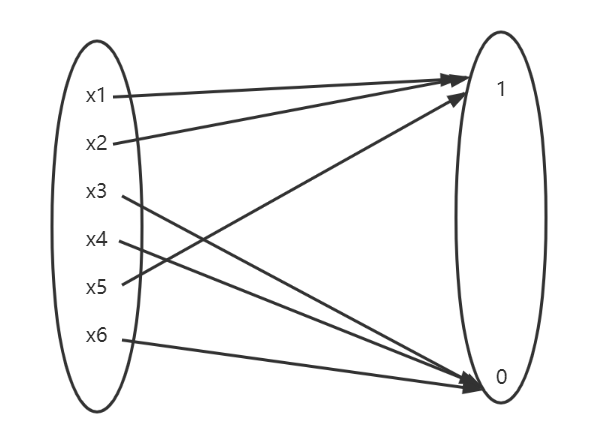
特征函数满足:
- χ ( A ∪ B ) ( x ) = χ A ( x ) ∨ χ B ( x ) ; χ_{(A∪B)} (x)=χ_A (x)∨χ_B (x); χ(A∪B)(x)=χA(x)∨χB(x);
- χ ( A ∩ B ) ( x ) = χ A ( x ) ∧ χ B ( x ) ; χ_{(A∩B)} (x)=χ_A (x)∧χ_B (x); χ(A∩B)(x)=χA(x)∧χB(x);
- χ ( A c ) ( x ) = 1 − χ A ( x ) χ_{(A^c )} (x)=1-χ_A (x) χ(Ac)(x)=1−χA(x)
特征函数中函数值仅仅取0,1两个值,缺少量化程度。
对于模糊概念,在数学上定义成为论域U的模糊子集。
1.2.模糊概念
1.2.1 特征函数的缺点

秃头悖论:头上掉一根头发,不是秃头;再掉一根,也不是秃头……按照此逻辑下去当秃头出现的时候还不是秃头。
这说明了使用非零即一的特征函数直接描述会造成程度化不足的问题
如何将不同的程度引入到特征函数中,使特征函数能够描述模糊概念?
将数字0,1转换为闭区间 [ 0 , 1 ] [0,1] [0,1]
1.2.2 隶属度函数
设U是论域,称映射 A ( x ) : U → [ 0 , 1 ] A(x):U\rightarrow [0,1] A(x):U→[0,1]为U上的一个模糊子集A。
映射 A ( x ) A(x) A(x)称为A的隶属函数,它表示 x x x对 A A A的隶属程度。
拿上面的秃头悖论的例子来说,秃头的论域U怎么选取? U = { 0 , 1 , 2 , 3 … … , 100000 } U = \{0,1,2,3……,100000\} U={0,1,2,3……,100000}
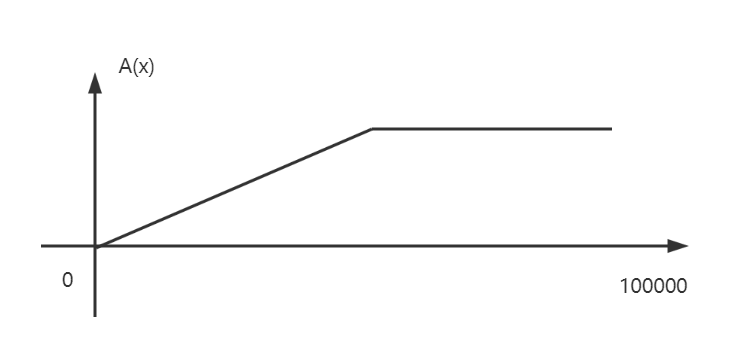
这个隶属度函数满足单调递增:头发越多,越不秃头。
中年人的隶属度函数与图像?
A ( x ) = { 1 , x i ∈ ( 18 , 35 ) ? , x i ∉ ( 18 , 35 ) A(x)=\begin{cases} 1,x_i∈(18,35)\\?,x_i∉(18,35) \end{cases} A(x)={1,xi∈(18,35)?,xi∈/(18,35)
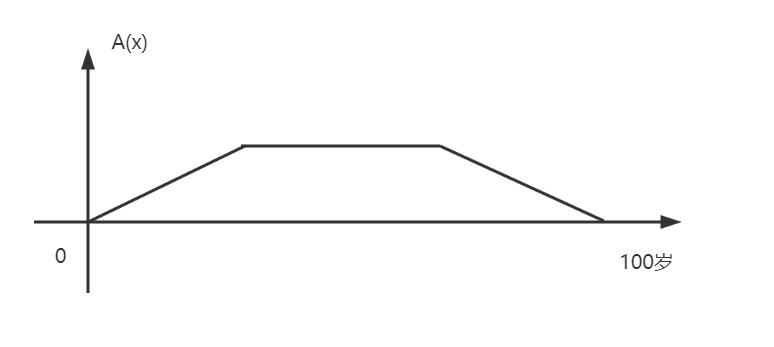
隶属度函数还存在着一些问题:如何确定隶属度函数?哪种的隶属度函数比较好?
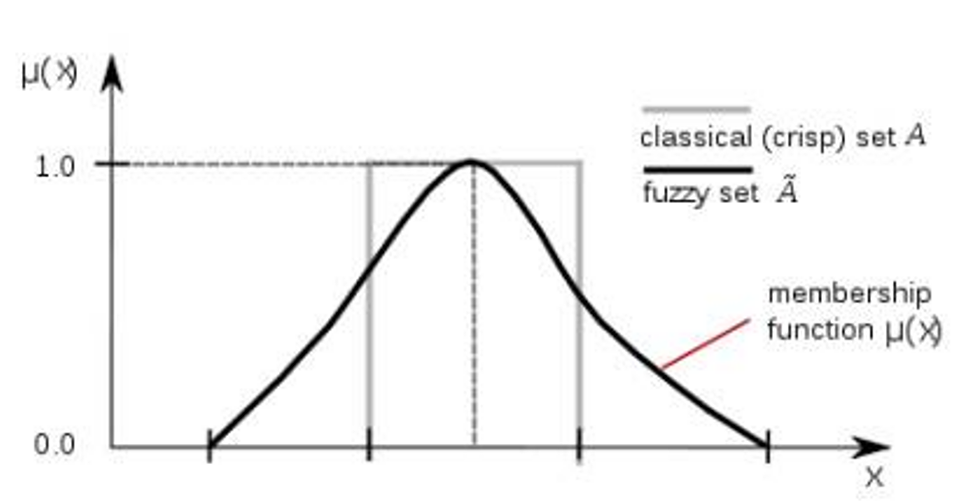
当A(x)= 0.5时,点x最具模糊性:偏向不明确——到0和1距离都是一样的。
当映射A(x)只取0或者1时,模糊子集A就是经典子集,而A(x)就是它的特征函数。可见经典子集是模糊子集的特殊情形。
- 隶属度函数的表示方法
例1 设论域U = {x1, x2, x3, x4, x5}(商品集),在U上定义一个模糊集:A =“质量好的商品”。
表 示 方 法 1 : A = ( 0.8 , 0.55 , 0 , 0.3 , 0.1 , 1 ) 表 示 方 法 2 : A = 0.8 x 1 + 0.55 x 2 + 0 x 3 + 0.3 x 4 + 1 x 5 表示方法1:A=(0.8,0.55,0,0.3,0.1,1)\\ 表示方法2:A=\frac{0.8}{x_1}+\frac{0.55}{x_2}+\frac{0}{x_3}+\frac{0.3}{x_4}+\frac{1}{x_5} 表示方法1:A=(0.8,0.55,0,0.3,0.1,1)表示方法2:A=x10.8+x20.55+x30+x40.3+x51
方法2是用积分的形式来表示,对于 x 4 x_4 x4是好商品的程度是0.3
表示法3:
1.3 模糊集的运算
相等: A = B ⇔ A ( x ) = B ( x ) A=B\Leftrightarrow A(x) = B(x) A=B⇔A(x)=B(x),每一个点的隶属度相等
包含: A 含 于 B ⇔ A ( x ) ≤ B ( x ) A含于B\Leftrightarrow A(x)≤B(x) A含于B⇔A(x)≤B(x)
并:A∪B的隶属函数, μ ( A ∪ B ) ( x ) = μ A ( x ) ∪ μ B ( x ) \mu_{(A∪B)} (x)= \mu_A(x)∪\mu_B(x) μ(A∪B)(x)=μA(x)∪μB(x)
交,补运算也是一样的。
模糊集的运算性质基本与经典集合一致,除了排中律以外:
A ∪ A c ≠ U A∪A^c≠U\\ A∪Ac=U
模糊集不再具有非此即彼的特征。
1.4 λ \lambda λ截集
模糊集的 λ − \lambda- λ−截集 A λ A_{\lambda} Aλ是一个经典集合,由隶属度不小于 λ \lambda λ的成员构成。即:
A λ = { x ∣ A ( x ) ≥ λ } A_{\lambda} = \{x|A(x)≥\lambda\} Aλ={x∣A(x)≥λ}
例3:论域U={u1, u2, u3, u4 , u5 , u6}(学生集),他们的成绩依次为50,60,70,80,90,95,A=“学习成绩优秀的学生”的隶属度分0.5,0.6,0.7,0.8,0.9,0.95, 则 A 0.9 = u 5 , u 6 A_{0.9}={u5 , u6} A0.9=u5,u6。
显而易见的是, λ \lambda λ越大,截集中的元素越少;也有: λ 1 ≤ λ 2 \lambda_1≤\lambda_2 λ1≤λ2,则有 A λ 2 含 于 A λ 2 A_{\lambda_2}含于A_{\lambda_2} Aλ2含于Aλ2
2.模糊关系
思路:经典子集 → \rightarrow →模糊子集;经典关系 → \rightarrow →模糊关系
2.1经典二元关系
什么是经典关系?一般用R表示
U上的一个经典二元关系R,在数学上可以定义为U和U的笛卡尔乘积的经典子集
设R为一个从有限集合X(m个元素)到有限集合Y(n个元素)的模糊关系,则R对应的模糊矩阵定义如下:
R m × n ( i , j ) = R ( x i , y j ) R_{m\times n}(i,j) = R(x_i,y_j) Rm×n(i,j)=R(xi,yj)
这个关系矩阵本身就是一个映射。
2.2 模糊关系
设有论域X,Y,X ´ Y 的一个模糊子集 R 称为从 X 到 Y 的模糊关系。模糊子集 R 的隶属函数为映射
R : X × Y → [ 0 , 1 ] R:X\times Y\rightarrow [0,1] R:X×Y→[0,1]
特别地,当 X =Y 时,称之为 X 上各元素之间的模糊关系.
例4:"长得像"U:{父亲,母亲,儿子,女儿},定义U上的二元模糊关系:“相像”
这个相像关系的矩阵一定是一个对角线为1的对称矩阵,比如:
1 0.6 0.7 0.8 0.6 1 0.9 0.75 0.7 0.9 1 0.65 0.8 0.75 0.65 1 \begin{matrix} 1&0.6&0.7&0.8\\ 0.6&1&0.9&0.75\\ 0.7&0.9&1&0.65\\ 0.8&0.75&0.65&1 \end{matrix} 10.60.70.80.610.90.750.70.910.650.80.750.651
2.2.1模糊关系的运算
模糊关系之间的运算就是模糊子集的运算,具有相同的性质。
2.2.2模糊关系的合成
当论域为有限时,模糊关系的合成可以用其对应模糊矩阵的乘法来实现.只不过这里的模糊矩阵的乘法不同于常规矩阵的乘积,但模式是一样的。
经典矩阵的乘法:对应相乘后相加
模糊矩阵的乘法:对应取小后取大
模糊矩阵乘法程序如下:
function res = fuzzy_rela_cal(matrix)
%FUZZY 计算矩阵自身与自身的模糊关系矩阵
% 模糊矩阵的乘法与一般的乘法不同,先取大后取小
n=length(matrix);
res = zeros(n,n);
for i=1:nfor j=1:nres(i,j)=max(min([matrix(i,:);matrix(:,j)']));end
endend
2.2.3 模糊关系的特性
- 自反性:主对角线上的元素为1
- 对称性:模糊矩阵为对称阵
- 传递性:R具有传递性当且仅当 R 2 含 于 R R^2含于R R2含于R
如果模糊关系R是X上各元素之间的模糊关系,且满足上面的三个特性,则称模糊关系是一个经典的模糊等价关系
经典等价关系的作用:划分
若R是U上的一个经典等价二元关系,可以得到一个等价类/划分 { [ x ] ∣ x ∈ U } \{[x]|x∈U\} {[x]∣x∈U}
如有下面的关系矩阵:
μ 1 μ 2 μ 3 μ 1 1 0 1 μ 2 0 1 0 μ 3 1 0 1 \begin{matrix} &\mu_1&\mu_2&\mu_3\\ \mu_1&1&0&1\\ \mu_2&0&1&0\\ \mu_3&1&0&1\\ \end{matrix} μ1μ2μ3μ1101μ2010μ3101
如何判断是否是一个等价关系?
- 对角线是1:自反性
- 对称矩阵:对称性
- 和自己进行合成(模糊矩阵计算方式),结果相等:传递性
按照上面三个标准,若都满足,则是一个等价关系。
2.2.3模糊等价关系和经典等价关系的联系
定理1:R是模糊等价关系当且经当R的任意 λ − \lambda- λ−截集都是经典等价关系。
μ 1 μ 2 μ 3 μ 1 0.2 0.3 0.5 μ 2 0 1 0.9 μ 3 0.3 0.5 0.7 \begin{matrix} &\mu_1&\mu_2&\mu_3\\ \mu_1&0.2&0.3&0.5\\ \mu_2&0&1&0.9\\ \mu_3&0.3&0.5&0.7\\ \end{matrix} μ1μ2μ3μ10.200.3μ20.310.5μ30.50.90.7
上面的矩阵对应的 λ = 0.4 \lambda=0.4 λ=0.4时的截集如下:
μ 1 μ 2 μ 3 μ 1 0 0 1 μ 2 0 1 1 μ 3 0 1 1 \begin{matrix} &\mu_1&\mu_2&\mu_3\\ \mu_1&0&0&1\\ \mu_2&0&1&1\\ \mu_3&0&1&1\\ \end{matrix} μ1μ2μ3μ1000μ2011μ3111
上面的矩阵不满足三个性质,所以不是经典等价关系。
存在截集 λ = 0.4 \lambda=0.4 λ=0.4时,不满足定理1,所以R不是一个模糊等价关系。
3.模糊聚类
聚类的前提条件:在某一方面具有相似性
3.1模糊相似关系
R 是 X 上各元素之间的模糊关系,若R 满足:对于任意的x,y,满足
- (1) 自反性:R( x , x ) = 1;
- (2) 对称性:R( x , y ) = R( y , x ) ,
则称模糊关系 R 是 X 上的一个模糊相似关系.
模糊相似关系未必是模糊等价关系:相差一个传递性。
3.2模糊聚类的关键
步骤:
- 得到模糊相似关系
- 由模糊相似关系出发得到模糊等价关系
- 由模糊等价关系的 λ − \lambda- λ−截集得到等价关系,从而分类
3.2.1 数据标准化
- 平移,标准差变换
- 平移,极差变换
通过上面的方式将数据映射到[0,1]上
原始矩阵---->模糊相似关系:模型很多,不同的模型得到的模糊相似关系也不一样。
查阅资料,选择合适的方式将初始的矩阵转换为模糊相似关系的方法。
定理2 若R是模糊相似矩阵,则对任意的自然数k, R k R^k Rk 也是模糊相似矩阵
定理3:若R是n阶模糊相似矩阵,则存在一个最小自然数k(k≤n),对于一切大于k的自然数 l l l,恒有 R l = R k R^l = R^k Rl=Rk,即 R k R^k Rk是模糊等价矩阵( R 2 k = R k R^{2k}=R^k R2k=Rk)。此时,称 R k R^k Rk为R的传递闭包,记作 t ( R ) = R k t(R) = R^k t(R)=Rk。
上述定理表明,任一个模糊相似矩阵可诱导出一个模糊等价矩阵。
使用平方法求传递闭包:
R → R 2 → R 4 → R 8 → R 16 … … R\rightarrow R^2\rightarrow R^4\rightarrow R^8\rightarrow R^{16}…… R→R2→R4→R8→R16……
最后由模糊等价关系的 λ \lambda λ截集得到等价关系,从而分类。不同的 λ \lambda λ得到的分类可能是不一样的。
3.3 模糊聚类方法及步骤
Step1:数据预处理:标准化
(1)获取数据
设论域 X = x 1 , x 2 , . . . , x n X = {x_1,x_2,...,x_n} X=x1,x2,...,xn为被分类的对象,每个对象又由 m 个指标表示其性态, x i x_i xi的观测值
e i = ( x i 1 , x i 2 , . . . , x i m ) e_i=(x_{i1},x_{i2},...,x_{im}) ei=(xi1,xi2,...,xim)
于是可以得到原始数据矩阵 A = ( x i j ) n × m A=(x_{ij})_{n\times m } A=(xij)n×m
(2)数据标准化处理
目的:消除不同的数据的量纲的影响
①平移-标准差变换
x i j ′ = x i j − x ^ j s j ( i = 1 , 2 , . . . , n ; j = 1 , 2 , . . . , m ) x_{ij}^{'}=\frac{x_{ij}-\hat x_{j}}{s_j}\qquad (i=1,2,...,n; j=1,2,...,m)\\ xij′=sjxij−x^j(i=1,2,...,n;j=1,2,...,m)
其中:
x ^ j = 1 n ∑ i = 1 n x i j , s j = [ 1 n − 1 ∑ ( x i j − x ^ j ) 2 ] 1 2 ( j = 1 , 2 , . . . , m ) \hat x_j=\frac{1}{n}\sum\limits_{i=1}^{n}x_{ij}, s_j=[\frac{1}{n-1}\sum\limits(x_{ij}-\hat x_j)^2]^{\frac{1}{2}}\qquad (j=1,2,...,m) x^j=n1i=1∑nxij,sj=[n−11∑(xij−x^j)2]21(j=1,2,...,m)
matlab代码:
②平移-极差变换
如果经过平移—标准差变换后还有某些 x i j ’ ∉ [ 0 , 1 ] x_{ij}’ ∉ [0,1] xij’∈/[0,1],则还需对其进行平移—极差变换,即
x i j ′ ′ = x i j ’ − min 1 ≤ i ≤ n { x i j ’ } max 1 ≤ i ≤ n { x i j ’ } − min 1 ≤ i ≤ n { x i j ’ } 其 中 , ( j = 1 , 2 , . . . , m ) x_{ij}''=\frac{x_{ij}’-\min\limits_{1≤i≤n}\{x_{ij}’\}}{\max\limits_{1≤i≤n}\{x_{ij}’\}-\min\limits_{1≤i≤n}\{x_{ij}’\}}\qquad其中,(j=1,2,...,m) xij′′=1≤i≤nmax{xij’}−1≤i≤nmin{xij’}xij’−1≤i≤nmin{xij’}其中,(j=1,2,...,m)
程序①:
function result = trans_standard(Matrix)
%TARNS_STANDARD 进行平移-标准差变换
% 将聚类的数据进行预处理,使其满足自反性和对称性
[m, n] = size(Matrix); %m行,n列
xj_hat = mean(Matrix, 1); %求每一列的均值\hat x_j
sj = std(Matrix,0,1); %无偏估计,求出每一列的标准差s_j
result = zeros(m,n);for i = 1:mfor j = 1:nresult(i,j) = (Matrix(i,j) - xj_hat(j)) / sj(j);end
end
end
这样,所有的 x i j ′ ′ ∈ [ 0 , 1 ] x_{ij}''∈[0,1] xij′′∈[0,1],且也不存在量纲因素的影响,从而可以得到模糊矩阵
R = ( x i j ′ ′ ) n × m R=(x_{ij}'')_{n\times m} R=(xij′′)n×m
程序②:
function result = trans_max_min(Matrix)
% 进行平移—极差变换
% 经过平移—标准差变换后还有某些矩阵元素不在0,1上,将数据标准化到区间0-1上
[m, n] = size(Matrix);
[min_xij, ~] = min(Matrix);
[max_xij, ~] = max(Matrix);
result = Matrix;
for i = 1:mfor j = 1:nresult(i, j) = (Matrix(i,j) - min_xij(j)) / (max_xij(j) - min_xij(j));end
end
end
Step2:建立模糊相似矩阵
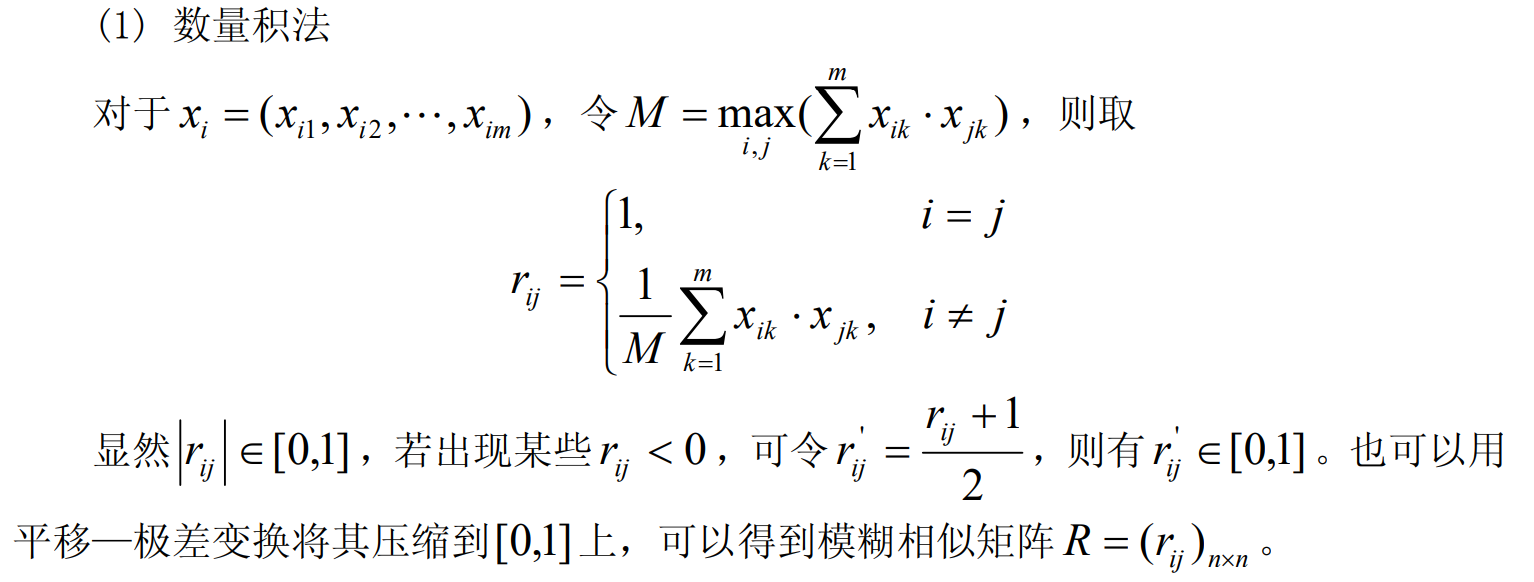
(2)夹角余弦法

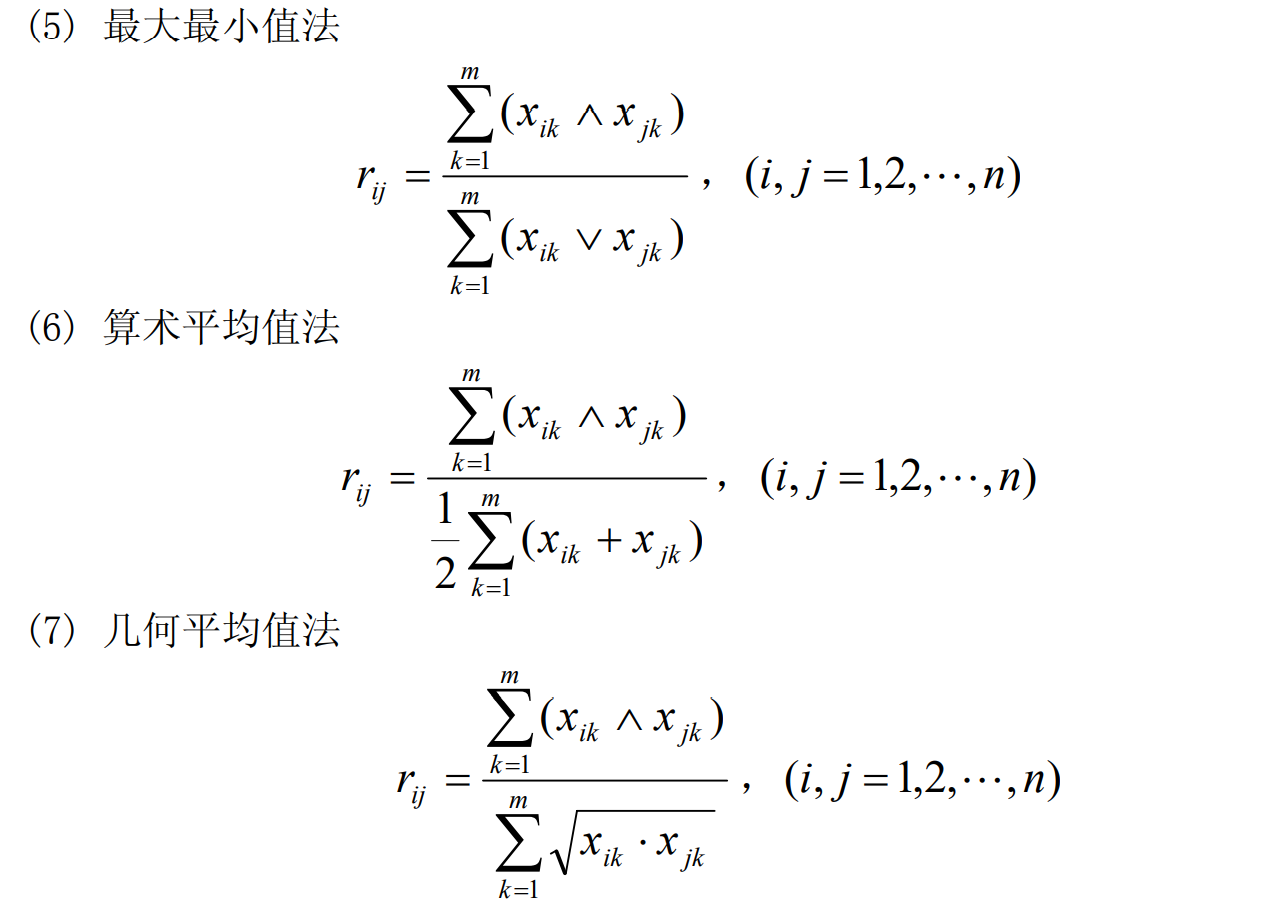
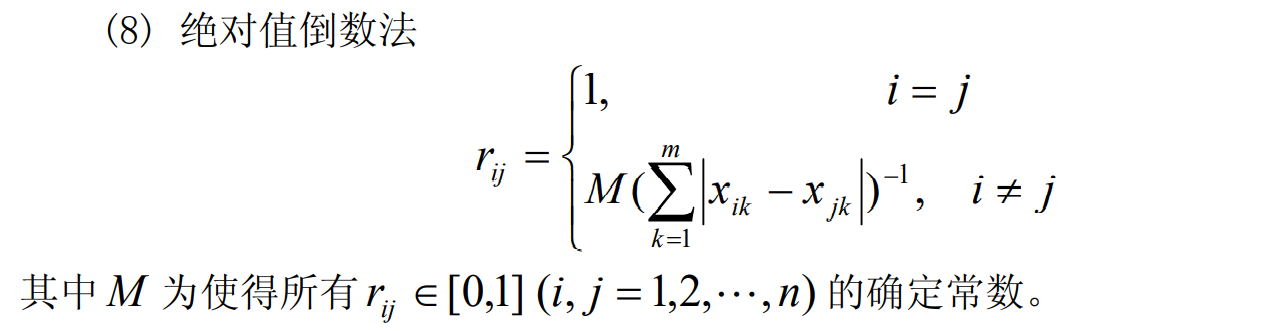
这里只给出相关系数法的函数:
function result = cosine_of_angle(matrix)
%COSINE_OF_ANGLE 夹角余弦法构造模糊相似矩阵
[n,m] = size(matrix);
result = zeros(n,n);
pre = matrix.*matrix;
for i = 1:nfor j = 1:ntemp = matrix(i,:).*matrix(j,:);fenzi = abs(sum(temp));fenmu = sum(pre(i,:))*sum(pre(j,:));fenmu = fenmu^(0.5);result(i,j) = fenzi/fenmu;end
endendStep3:聚类
所谓聚类方法就是依据模糊矩阵将所研究的对象进行分类的方法。对于不同的置信水平λ ∈[0,1],可以得到不同的分类结果,从而形成动态聚类图。常用的方法如下:
(1)传递闭包法
Step2 中求出的模糊相似矩阵 R 出发,来构造一个模糊等价矩阵 R ∗ R^* R∗ 。其方法就 是用平方法求出 R 的传递闭包t® ,则 t ( R ) = R ∗ t(R) = R^* t(R)=R∗;然后,由大到小取一组λ ∈[0,1] , 确定相应的λ 截矩阵,则可以将其分类,同时也可以构成动态聚类图。
传递闭包程序:
function result = transitive_closure(matrix)
%TRANSITIVE_CLOSURE 利用传递闭包法求模糊相似矩阵得到的模糊等价矩阵
% 利用传递闭包法将输入的模糊相似矩阵构造成一个模糊等价矩阵,用于不同lambda下的分类
[m,~] = size(matrix);
max_times = floor(log2(m))+1; %最多迭代max_times可结束。
times = 0;
res0 = matrix;
res1 = fuzzy_rela_cal(matrix);
for i = 0:30if(res0 == res1)break;endres0 = res1;res1 = fuzzy_rela_cal(res0);
end
result = res0;end
模糊关系合成函数fuzzy_rela_cal.m
function res = fuzzy_rela_cal(matrix)
%FUZZY 计算矩阵自身与自身的模糊关系矩阵
% 模糊矩阵的乘法与一般的乘法不同,先取大后取小
n=length(matrix);
res = zeros(n,n);
for i=1:nfor j=1:nres(i,j)=max(min([matrix(i,:);matrix(:,j)']));end
endend
3.4应用案例(作业)
这里案例直接采用司守奎《数学建模算法与应用》中的例题:
例 15 某地区内有 12 个气象观测站,10 年来各站测得的年降水量如表 3 所示。 为了节省开支,想要适当减少气象观测站,试问减少哪些观察站可以使所得到的降水量 信息仍然足够大?
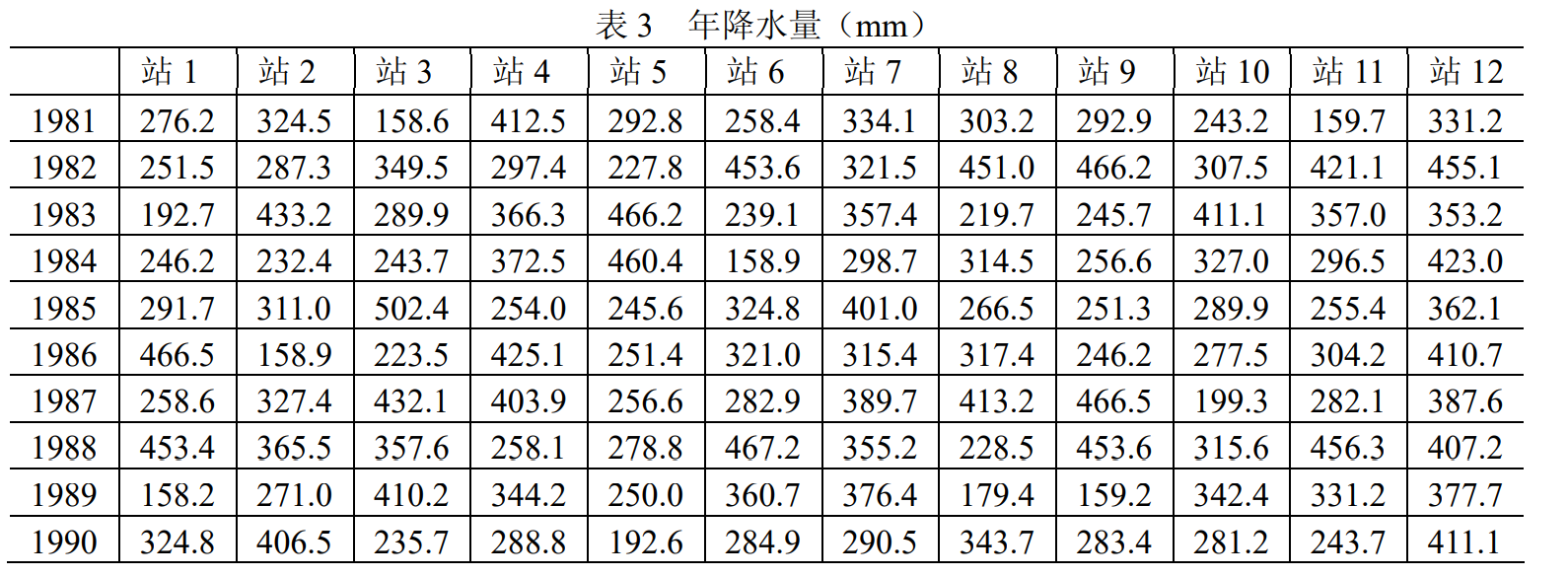
(数据后续会放在附件中)
- 数据初始化处理
由于题目要求是对站点进行聚类,所以我们在程序中对矩阵进行了转置。
我们首先对数据进行标准化处理(其实这里的数据不需要进行标准换处理,因为量纲都是一样的),采取平移-标准差变化和平移-极差变换得到下面的标准化后的矩阵:
| 0.463174 | 0.099413 | 0 | 0.289552 | 0.179517 | 1 | 0.221931 | 0.942187 | 0 | 0.605034 | |
| 0.653407 | 0.249581 | 0.879342 | 0.243781 | 0.254673 | 0 | 0.479416 | 0.573942 | 0.447619 | 0.978947 | |
| 0 | 0.510487 | 0.355393 | 0.28126 | 1 | 0.210013 | 0.871257 | 0.540846 | 1 | 0.197254 | |
| 1 | 0.291946 | 0.634735 | 0.708458 | 0.03271 | 0.86541 | 0.765719 | 0.124005 | 0.738095 | 0.440275 | |
| 0.528555 | 0 | 1 | 1 | 0 | 0.300715 | 0.214446 | 0.210725 | 0.364286 | 0 | |
| 0.393068 | 0.947148 | 0.169653 | 0 | 0.308411 | 0.526983 | 0.312874 | 1 | 0.803571 | 0.422426 | |
| 0.691217 | 0.393037 | 0.602194 | 0.463682 | 0.60514 | 0.508778 | 0.712575 | 0.530792 | 0.865873 | 0.448055 | |
| 0.569516 | 0.936242 | 0.09872 | 0.516086 | 0.081386 | 0.51528 | 0.800524 | 0 | 0.084127 | 0.691533 | |
| 0.528948 | 1 | 0.193784 | 0.324046 | 0.022196 | 0.28381 | 1 | 0.943025 | 0.003968 | 0.415561 | |
| 0.333202 | 0.334312 | 0.798537 | 0.557546 | 0.172508 | 0.385566 | 0 | 0.364893 | 0.730952 | 0.405492 | |
| 0.004332 | 0.810822 | 0.600731 | 0.456385 | 0.038162 | 0.472367 | 0.30988 | 0.954336 | 0.686508 | 0.233867 | |
| 0.679795 | 0.95344 | 0.586837 | 0.875954 | 0.45366 | 0.818596 | 0.704716 | 0.748638 | 0.871032 | 1 |
进行数据初始化的程序:
clear
clc
%% 模糊聚类
a=[276.2 324.5 158.6 412.5 292.8 258.4 334.1 303.2 292.9 243.2 159.7 331.2
251.5 287.3 349.5 297.4 227.8 453.6 321.5 451.0 466.2 307.5 421.1 455.1
192.7 433.2 289.9 366.3 466.2 239.1 357.4 219.7 245.7 411.1 357.0 353.2
246.2 232.4 243.7 372.5 460.4 158.9 298.7 314.5 256.6 327.0 296.5 423.0
291.7 311.0 502.4 254.0 245.6 324.8 401.0 266.5 251.3 289.9 255.4 362.1
466.5 158.9 223.5 425.1 251.4 321.0 315.4 317.4 246.2 277.5 304.2 410.7
258.6 327.4 432.1 403.9 256.6 282.9 389.7 413.2 466.5 199.3 282.1 387.6
453.4 365.5 357.6 258.1 278.8 467.2 355.2 228.5 453.6 315.6 456.3 407.2
158.2 271.0 410.2 344.2 250.0 360.7 376.4 179.4 159.2 342.4 331.2 377.7
324.8 406.5 235.7 288.8 192.6 284.9 290.5 343.7 283.4 281.2 243.7 411.1];
a = a';
result = trans_standard(a); %平移-标准差变换
initial_mat = trans_max_min(result); %平移—极差变换
function result = trans_standard(Matrix)
%TARNS_STANDARD 进行平移-标准差变换
% 将聚类的数据进行预处理,使其满足自反性和对称性
[m, n] = size(Matrix); %m行,n列
xj_hat = mean(Matrix, 1); %求每一列的均值\hat x_j
sj = std(Matrix,0,1); %无偏估计,求出每一列的标准差s_j
result = zeros(m,n);for i = 1:mfor j = 1:nresult(i,j) = (Matrix(i,j) - xj_hat(j)) / sj(j);end
end
end
function result = trans_max_min(Matrix)
% 进行平移—极差变换
% 经过平移—标准差变换后还有某些矩阵元素不在0,1上,将数据标准化到区间0-1上
[m, n] = size(Matrix);
[min_xij, ~] = min(Matrix);
[max_xij, ~] = max(Matrix);
result = Matrix;
for i = 1:mfor j = 1:nresult(i, j) = (Matrix(i,j) - min_xij(j)) / (max_xij(j) - min_xij(j));end
end
end- 模糊相似矩阵合成
这里使用夹角余弦法进行构造,程序如下:
result = cosine_of_angle(initial_mat); %使用夹角余弦法构造模糊等价矩阵
function result = cosine_of_angle(matrix)
%COSINE_OF_ANGLE 夹角余弦法构造模糊相似矩阵
[n,m] = size(matrix);
result = zeros(n,n);
pre = matrix.*matrix;
for i = 1:nfor j = 1:ntemp = matrix(i,:).*matrix(j,:);fenzi = abs(sum(temp));fenmu = sum(pre(i,:))*sum(pre(j,:));fenmu = fenmu^(0.5);result(i,j) = fenzi/fenmu;end
endend
此时,模糊矩阵已经具有了自反性和对称性。
- 模糊等价矩阵合成
矩阵不具有传递性,也就不是模糊等价矩阵。使用传递闭包法构造模糊等价矩阵。程序如下:
result = transitive_closure(result);
function result = transitive_closure(matrix)
%TRANSITIVE_CLOSURE 利用传递闭包法求模糊相似矩阵得到的模糊等价矩阵
% 利用传递闭包法将输入的模糊相似矩阵构造成一个模糊等价矩阵,用于不同lambda下的分类
[m,~] = size(matrix);
max_times = floor(log2(m))+1; %最多迭代max_times可结束。
times = 0;
res0 = matrix;
res1 = fuzzy_rela_cal(matrix);
for i = 0:30if(res0 == res1)break;endres0 = res1;res1 = fuzzy_rela_cal(res0);
end
result = res0;end
此时已经得到了模糊等价矩阵,矩阵如下:
| 1 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | 0.750007 | |
| 0.750007 | 1 | 0.846123 | 0.846123 | 0.83726 | 0.846123 | 0.846123 | 0.846123 | 0.830829 | 0.846123 | 0.846123 | 0.846123 | |
| 0.750007 | 0.846123 | 1 | 0.869408 | 0.83726 | 0.861438 | 0.869408 | 0.849058 | 0.830829 | 0.869408 | 0.861438 | 0.869408 | |
| 0.750007 | 0.846123 | 0.869408 | 1 | 0.83726 | 0.861438 | 0.896658 | 0.849058 | 0.830829 | 0.875018 | 0.861438 | 0.896658 | |
| 0.750007 | 0.83726 | 0.83726 | 0.83726 | 1 | 0.83726 | 0.83726 | 0.83726 | 0.830829 | 0.83726 | 0.83726 | 0.83726 | |
| 0.750007 | 0.846123 | 0.861438 | 0.861438 | 0.83726 | 1 | 0.861438 | 0.849058 | 0.830829 | 0.861438 | 0.893002 | 0.861438 | |
| 0.750007 | 0.846123 | 0.869408 | 0.896658 | 0.83726 | 0.861438 | 1 | 0.849058 | 0.830829 | 0.875018 | 0.861438 | 0.935876 | |
| 0.750007 | 0.846123 | 0.849058 | 0.849058 | 0.83726 | 0.849058 | 0.849058 | 1 | 0.830829 | 0.849058 | 0.849058 | 0.849058 | |
| 0.750007 | 0.830829 | 0.830829 | 0.830829 | 0.830829 | 0.830829 | 0.830829 | 0.830829 | 1 | 0.830829 | 0.830829 | 0.830829 | |
| 0.750007 | 0.846123 | 0.869408 | 0.875018 | 0.83726 | 0.861438 | 0.875018 | 0.849058 | 0.830829 | 1 | 0.861438 | 0.875018 | |
| 0.750007 | 0.846123 | 0.861438 | 0.861438 | 0.83726 | 0.893002 | 0.861438 | 0.849058 | 0.830829 | 0.861438 | 1 | 0.861438 | |
| 0.750007 | 0.846123 | 0.869408 | 0.896658 | 0.83726 | 0.861438 | 0.935876 | 0.849058 | 0.830829 | 0.875018 | 0.861438 | 1 |
- 聚类
最后我们构造lambda截集,进行聚类
lambda = 0.85;
res = zeros(length(a),length(a));
res = lambda_(result, lambda);
function res = fuzzy_rela_cal(matrix)
%FUZZY 计算矩阵自身与自身的模糊关系矩阵
% 模糊矩阵的乘法与一般的乘法不同,先取大后取小
n=length(matrix);
res = zeros(n,n);
for i=1:nfor j=1:nres(i,j)=max(min([matrix(i,:);matrix(:,j)']));end
endend
function result = lambda_(matrix, lambda)
%LAMBDA_ 聚类,返回聚类矩阵
% 根据参数lambda返回lambda截集下的经典矩阵,并且实现分类
m = length(matrix);
result = zeros(m,m);
result(matrix>=lambda) = 1;
end
经过上面的步骤,我们得到 λ = 0.85 \lambda=0.85 λ=0.85时的矩阵:
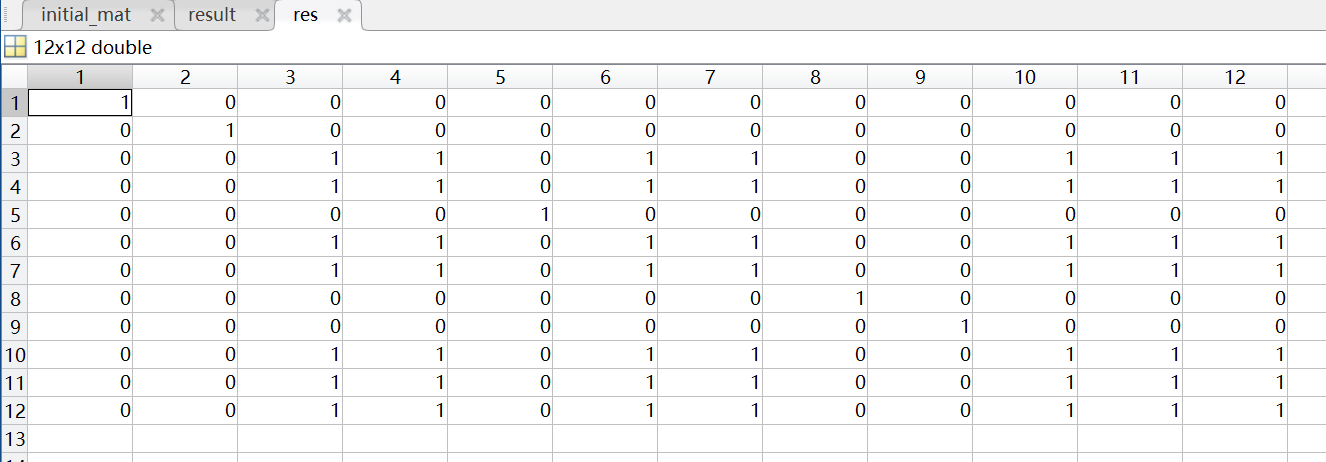
从矩阵可以看出分类情况为:
{ 站 1 } ∪ { 站 2 } ∪ { 站 3 , 站 4 , 站 6 , 站 7 , 站 10 , 站 11 , 站 12 } ∪ { 站 5 } ∪ { 站 8 } ∪ { 站 9 } \{站1\}∪\{站2\}∪\{站3,站4,站6,站7,站10,站11,站12\}∪\{站5\}∪\{站8\}∪\{站9\} {站1}∪{站2}∪{站3,站4,站6,站7,站10,站11,站12}∪{站5}∪{站8}∪{站9}
即为最后的聚类结果。
da);
```matlab
function res = fuzzy_rela_cal(matrix)
%FUZZY 计算矩阵自身与自身的模糊关系矩阵
% 模糊矩阵的乘法与一般的乘法不同,先取大后取小
n=length(matrix);
res = zeros(n,n);
for i=1:nfor j=1:nres(i,j)=max(min([matrix(i,:);matrix(:,j)']));end
endend
function result = lambda_(matrix, lambda)
%LAMBDA_ 聚类,返回聚类矩阵
% 根据参数lambda返回lambda截集下的经典矩阵,并且实现分类
m = length(matrix);
result = zeros(m,m);
result(matrix>=lambda) = 1;
end
经过上面的步骤,我们得到 λ = 0.85 \lambda=0.85 λ=0.85时的矩阵:
从矩阵可以看出分类情况为:
{ 站 1 } ∪ { 站 2 } ∪ { 站 3 , 站 4 , 站 6 , 站 7 , 站 10 , 站 11 , 站 12 } ∪ { 站 5 } ∪ { 站 8 } ∪ { 站 9 } \{站1\}∪\{站2\}∪\{站3,站4,站6,站7,站10,站11,站12\}∪\{站5\}∪\{站8\}∪\{站9\} {站1}∪{站2}∪{站3,站4,站6,站7,站10,站11,站12}∪{站5}∪{站8}∪{站9}
即为最后的聚类结果。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!