树形dp TT的苹果树

题意：

在大家的三连助攻下，TT 一举获得了超级多的猫咪，因此决定开一间猫咖，将快乐与大家一同分享。并且在开业的那一天，为了纪念这个日子，TT 在猫咖门口种了一棵苹果树。
一年后，苹果熟了，到了该摘苹果的日子了。
已知树上共有 N 个节点，每个节点对应一个快乐值为 w[i] 的苹果，为了可持续发展，TT 要求摘了某个苹果后，不能摘它父节点处的苹果。
TT 想要令快乐值总和尽可能地大，你们能帮帮他吗？

Input
结点按 1～N 编号。
第一行为 N (1 ≤ N ≤ 6000) ，代表结点个数。
接下来 N 行分别代表每个结点上苹果的快乐值 w[i]（-128 ≤ w[i] ≤ 127)。
接下来 N-1 行，每行两个数 L K，代表 K 是 L 的一个父节点。
输入有多组，以 0 0 结束。
Output
每组数据输出一个整数，代表所选苹果快乐值总和的最大值。

输入样例
7
1
1
1
1
1
1
1
1 3
7 4
2 3
4 5
6 4
3 5
0 0

输出样例
5

思路：

对于在树结构上进行的动态规划叫做树形dp，由于树的性质，一般采用递归进行。

对于这道题，按照要求采取的果子在树上的距离应该大于等于2，即采取了某个果子，那么这个果子的父节点和子节点都不能取。

dp[i][1/0]代表以i为节点的子树能达到的最大的气氛值，dp[i][1]代表i节点选了，dp[i][0]代表i节点没选，状态转移方程是

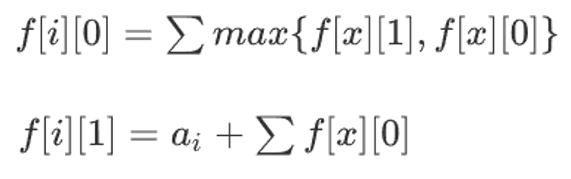
若是父节点选了，那么子节点一定不能选，若是父节点没选，子节点可选可不选。

为了减少调用函数的次数，即为了减少重复的对某个节点dp值得计算，设立一个数组vis[i][0/1]，vis[i][0] == true代表i号节点不选的值已经计算过，直接在数组中调用即可，vis[i][1] == true代表i号节点选则的值已经计算过。

代码：

#include
#include
#include
using namespace std;//dp[i][1/0]代表以i为节点的子树能达到的最大的气氛值
//dp[i][1]代表i节点选了
//dp[i][0]代表i节点没选struct Edge
{int v, next;
}edge[6005];int head[6005];long long tot;bool vis[6005][2];//[][0]代表不取，[][1]代表取void add(int u, int v)
{edge[tot].v = v;edge[tot].next = head[u];head[u] = tot;tot++;
}int dp[6005][2];
int w[6005];
bool isRoot[6005];void thisNotGet(int);void thisGet(int now)
{vis[now][1] = true;dp[now][1] += w[now];for (int i = head[now]; i != -1; i = edge[i].next){//子节点一定不能取if (vis[edge[i].v][0] == false)thisNotGet(edge[i].v);dp[now][1] += dp[edge[i].v][0];}
}void thisNotGet(int now)
{vis[now][0] = true;//下面可选可不选for (int i = head[now]; i != -1; i = edge[i].next){if (vis[edge[i].v][0] == false)thisNotGet(edge[i].v);if (vis[edge[i].v][1] == false)thisGet(edge[i].v);dp[now][0] += max(dp[edge[i].v][0], dp[edge[i].v][1]);}
}int main()
{int N;while (cin >> N){if (N == 0) {cin >> N;return 0;}tot = 0;memset(dp, 0, sizeof(dp));memset(head, -1, sizeof(head));memset(w, 0, sizeof(w));memset(isRoot, true, sizeof(isRoot));memset(vis, false, sizeof(vis));for (int i = 1; i <= N; i++)cin >> w[i];for (int i = 1; i < N; i++){int child, father;cin >> child >> father;add(father, child);isRoot[child] = false;}int root;for (int i = 1; i <= N; i++)if (isRoot[i])root = i;thisGet(root);thisNotGet(root);if (dp[root][0] > dp[root][1])cout << dp[root][0] << endl;else cout << dp[root][1] << endl;}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！