算法基础之数学知识模板
文章目录
- 一、质数
- 1.试除法判断质数
- 2.试除法分解质因数
- 3.筛法
- 二.约数
- 1.试除法求约数
- 2.约数个数
- 3.约数之和
- 4.最大公约数
- 三、欧拉函数
- 四、快速幂
- 五、拓展欧几里得算法
- 六、中国剩余定理
- 七、高斯消元法
- 八、组合数
- 1.递推
- 2.预处理
- 3.卢卡斯定理
- 4.高精度组合数
- 5.卡特兰数
- 九、容斥原理
- 十、博弈论
- 1.nim游戏
- 2.SG函数
- 十一、有趣的数学
一、质数
1.试除法判断质数
bool is_prime(int x)//最基础的方法
{int sqrt_x = sqrt(x);if(x < 2)return false;else{for(int i = 2; i <= sqrt_x; ++i)//或i <= n / iif(!(x % i))return false;return true;}
}
2.试除法分解质因数
void prime_resolve(int x)
{for (int i = 2; i <= x / i; ++ i){if(!(x % i)){//满足这个条件的i必为质数,因为如果i不是质数,比如i=4int cnt = 0;//那么当i=2时包含4,即包含2的部分已经被处理过了,所以能进入该判断的i必为质数while(!(x % i)){x /= i;++ cnt;}printf("%d %d\n", i, cnt);}}if(x > 1)printf("%d 1\n", x);//x中最多只含有一个大于sqrt(x)的质因子(反证法可知)puts("");
}
3.筛法
朴素筛法,O(nInn)
void get_prime(int n)
{for (int i = 2; i <= n; ++ i){if(!st[i])//标记为false则必为质数prime[cnt ++] = i;//cnt记录质数个数,prime记录有哪些质数for(int j = i + i; j <= n; j += i)//把i的倍数筛掉st[j] = true;}
}
埃式筛法,O(nloglogn)
void get_prime(int n)
{for (int i = 2; i <= n; ++ i){if(!st[i]){//与朴素筛法区别是只筛掉了质数的倍数,而后者把几乎所有数的倍数都筛了,且一个数n的质数个数不大于n/Innprime[cnt ++] = i;for(int j = i + i; j <= n; j += i)st[j] = true;}}
}
线性筛法,O(n)
void get_prime(int n)//线性筛,O(n),关键是保证每个合数都只被它的最小的质因数筛掉,这样就保证只筛一次,n个数即筛n次,所以是线性时间
{for (int i = 2; i <= n; ++ i){//因为是把所有素数都筛出来所以是2~nif(!st[i])prime[cnt ++] = i;for(int j = 0; prime[j] <= n / i; ++j){//当i很大时,n/i几乎小于1,即之后都不需要判断了,如果i是素数,则标记,如果i不是素数,那么之前小于等于sqrt(n)的某个素数一定会把i给筛掉(因为i很大了),所以直接跳过这步判断是没有问题的st[prime[j] * i] = true;//将prime[j]*i标记为合数, (1) i%pj == 0, pj定为i最小质因子,pj也定为pj*i最小质因子,因为prime[j]是从最小的素数开始的,所以prime[j]*i一定是被其最小的素数筛掉if(!(i % prime[j]))//一个数只筛一次的关键步骤,防止多筛,如12,当i=4时,如果没有i%prime[0]即i%2协助跳出循环,那么之后会发生i*prime[1]即4*3把12筛掉的情况,很明显12的最小质因数是2,这样会导致多筛;当i=6时,才能把6*prime[0]即12筛掉,break;//; (2) i%pj != 0, pj定小于i的所有质因子,所以pj也为pj*i最小质因子}}
}
二.约数
1.试除法求约数
vector<int> get_divisor(int x)
{vector<int> res;for(int i = 1; i <= x / i; ++ i){if(!(x % i)){res.push_back(i);if(x / i != i)//防止加入两个相同的数如7*7=49res.push_back(x / i);}}sort(res.begin(), res.end());return res;
}
2.约数个数
根据算术基本定理,任意合数 x = a 1 p 1 ∗ a 2 p 2 ∗ ⋅ ⋅ ⋅ ∗ a n p n x=a1^{p1}*a2^{p2}*···*an^{pn} x=a1p1∗a2p2∗⋅⋅⋅∗anpn(a1 有约数个数 N = ( p 1 + 1 ) ∗ ( p 2 + 1 ) ∗ ⋅ ⋅ ⋅ ∗ ( p n + 1 ) N=(p1+1)*(p2+1)*···*(pn+1) N=(p1+1)∗(p2+1)∗⋅⋅⋅∗(pn+1) 模板题 根据算术基本定理,任意合数 x = a 1 p 1 ∗ a 2 p 2 ∗ ⋅ ⋅ ⋅ ∗ a n p n x=a1^{p1}*a2^{p2}*···*an^{pn} x=a1p1∗a2p2∗⋅⋅⋅∗anpn(a1 由t=t∗a+1: 模板题 辗转相除法 线性筛求欧拉函数 模板题 证明:数学知识(2)44:00或知乎链接 二进制的思想理解快速幂 应用:求乘法逆元(逆元将除法转换成乘法) 裴蜀定理: 题解 递归复杂版 经过拓展欧几里得算法后可以得到方程的一组特解 ( x 0 , y 0 ) , d = g c d ( a , b ) (x0,y0),d=gcd(a,b) (x0,y0),d=gcd(a,b),即 a ∗ x 0 + b ∗ y 0 = d a*x0+b*y0=d a∗x0+b∗y0=d; 模板题 用拓展欧几里得算法解同余方程 先跳过,之后补上。。。 a,b小于2000时使用; 1 首先讲第一列的值都初始化成1,然后有递推公式: f [ i ] [ j ] = f [ i − 1 ] [ j ] + f [ i − 1 ] [ j − 1 ] f[i][j]=f[i-1][j]+f[i-1][j-1] f[i][j]=f[i−1][j]+f[i−1][j−1] 理解: a,b小于 1 0 5 10^5 105时使用; 模板题 a,b小于 1 0 18 10^{18} 1018时使用; 模板题 当题目中不允许取模而组合数太大且数量不多时使用; 模板题 a n s = C 2 n n − C 2 n n − 1 = C 2 n n n + 1 ans=C_{2n}^{n}-C_{2n}^{n-1}=\frac{C_{2n}^{n}}{n+1} ans=C2nn−C2nn−1=n+1C2nn 模板题 ⋃ i = 1 m S i = ( S 1 + S 2 + … + S i ) − ( S 1 ∩ S 2 + S 1 ∩ S 3 + … + S m − 1 ∩ S m ) + ( S 1 ∩ S 2 ∩ S 3 + … + S m − 2 ∩ S m − 1 ∩ S m ) + … + ( − 1 ) m − 1 ( ⋂ i = 1 m S ) \bigcup_{i=1}^m{S_i}=(S_1+S_2+…+S_i)-\left( S1\cap S2+S1\cap S3+…+S_{m−1}\cap S_m \right) +\left( S_1\cap S2\cap S3+…+S_{m−2}\cap S_{m−1}\cap S_m \right) +…+\left( -1 \right) ^{m-1}\left( \bigcap_{i=1}^m{S} \right) i=1⋃mSi=(S1+S2+…+Si)−(S1∩S2+S1∩S3+…+Sm−1∩Sm)+(S1∩S2∩S3+…+Sm−2∩Sm−1∩Sm)+…+(−1)m−1(i=1⋂mS) 模板题 nim游戏 先手必败状态: a 1 ⊕ a 2 ⊕ a 3 ⊕ ⋅ ⋅ ⋅ ⊕ a n = 0 a_1\oplus a_2\oplus a_3\oplus ···\oplus a_n=0 a1⊕a2⊕a3⊕⋅⋅⋅⊕an=0 模板题 大佬精彩博客 n条互不平行的直线的交点数为 n ∗ ( n − 1 ) / 2 n*(n-1)/2 n∗(n−1)/2
#include 3.约数之和
求 a 0 + a 1 + a 2 + ⋅ ⋅ ⋅ + a n a^0+a^1+a^2+···+a^n a0+a1+a2+⋅⋅⋅+an的关键步骤:while (p -- ) t = (t * a + 1) % mod;
t = 1 t=1 t=1
t = a + 1 t=a+1 t=a+1
t = a 2 + a + 1 t=a^2+a+1 t=a2+a+1
……
t = a p + a p − 1 + … + 1 t=a^p+a^{p−1}+…+1 t=ap+ap−1+…+1#include 4.最大公约数
int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}
三、欧拉函数
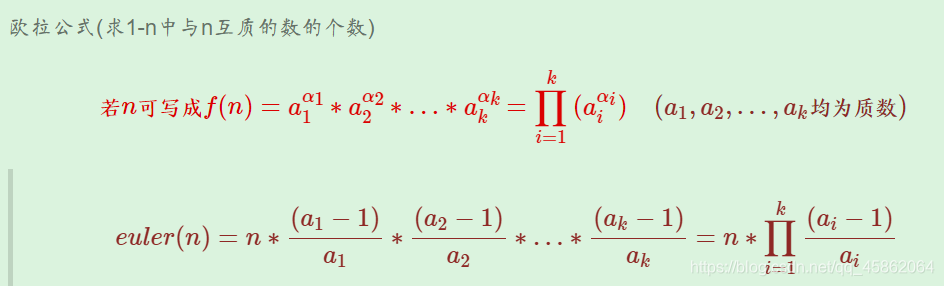

由定义求欧拉函数#include #include
欧拉定理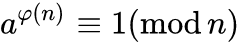
n为质数时则有费马小定理;四、快速幂
ll fm(int a, int k, int p)//求a^k%p
{ll res = 1;//任意数都可用二进制表示,所以k可以用01串表示while(k){//即a^k可用a^0*a^1*a^i*a^n表示,如2^5=2^(101)=2^4*2^1= 1*2^(100) * 0*2^(010) * 1*2*(001)if(k & 1)//如果二进制串的最后一位为1,表示需要乘以一个a,为0则不用管res =res * a % p;k >>= 1;//把二进制串当前位去掉a = (ll)a * a % p;//由于指数位数少了1,则表示底数应该平方,如3^4=3^(100), 指数100右移一位后, a^(10)=a^2 ,则a=3^2,即进行了平方}return res;
}

模板题五、拓展欧几里得算法
若a,b 是整数,且 g c d ( a , b ) = d gcd( a , b ) = d gcd(a,b)=d,那么对于任意的整数 x , y x , y x,y, a x + b y ax+by ax+by 都一定是 d的倍数,特别地,一定存在整数 x , y x,y x,y,使 a x + b y = d a x + b y = d ax+by=d成立
推论:对于方程 a x + b y = 1 ax+by=1 ax+by=1,只有当整数 a , b a , b a,b互质时,方程才有整数解。
应用:对于方程 a x + b y = z a x + b y = z ax+by=z,只有满足 g c d ( a , b ) ∣ z gcd ( a , b ) ∣ z gcd(a,b)∣z,方程才有整数解。
(设 g c d ( a , b ) = d ( a 1 x + b 1 y = d ) ) gcd(a,b)=d (a1x+b1y=d)) gcd(a,b)=d(a1x+b1y=d)),则两边同时扩大m倍,得 a x + b y = z ( 即 z = d ∗ m ) ax+by=z(即z=d*m) ax+by=z(即z=d∗m),所以要有 g c d ( a , b ) ∣ z gcd(a,b)|z gcd(a,b)∣z)
正常版:void exgcd(int a, int b, int &x, int &y)
{if(!b){x = 1;y = 0;}else{exgcd(b, a % b, x, y);int t = x;x = y;//x1 = y2y = t - a / b * y;}
}
void exgcd(int a, int b, int &x, int &y)
{if(!b){x = 1;y = 0;}else{//结合上个版本这里的递归看!exgcd(b, a % b, y, x);//由于引用,且x,y顺序对调,这里的y接收回溯的x,x接收回溯的y,即在这里y=x2,x=y2y -= a / b * x;//原本x1=y2,而这里由于x2=y2,所以x=x}
}
exgcd(a, b, x, y);
通解 x = x 0 − b / d ∗ k x=x0-b/d*k x=x0−b/d∗k
y = y 0 − b / d ∗ k y=y0-b/d*k y=y0−b/d∗k (因为 d d d是 b b b约数,所以 b / d b/d b/d
必为整数)
对于 a ∗ x 0 + m ∗ y 0 = g c d ( a , m ) a*x0+m*y0=gcd(a,m) a∗x0+m∗y0=gcd(a,m),左右两边同时乘以一个k后有 a ∗ x + m ∗ y = b a*x+m*y=b a∗x+m∗y=b,则 b / g c d ( a , m ) b/gcd(a,m) b/gcd(a,m)即为k,所以 x = x 0 ∗ k x=x0*k x=x0∗k#include 六、中国剩余定理
七、高斯消元法

模板题
题解八、组合数
1.递推
排列数可以看成是一个下三角,如
1 1
1 2 1
1 3 3 1
······
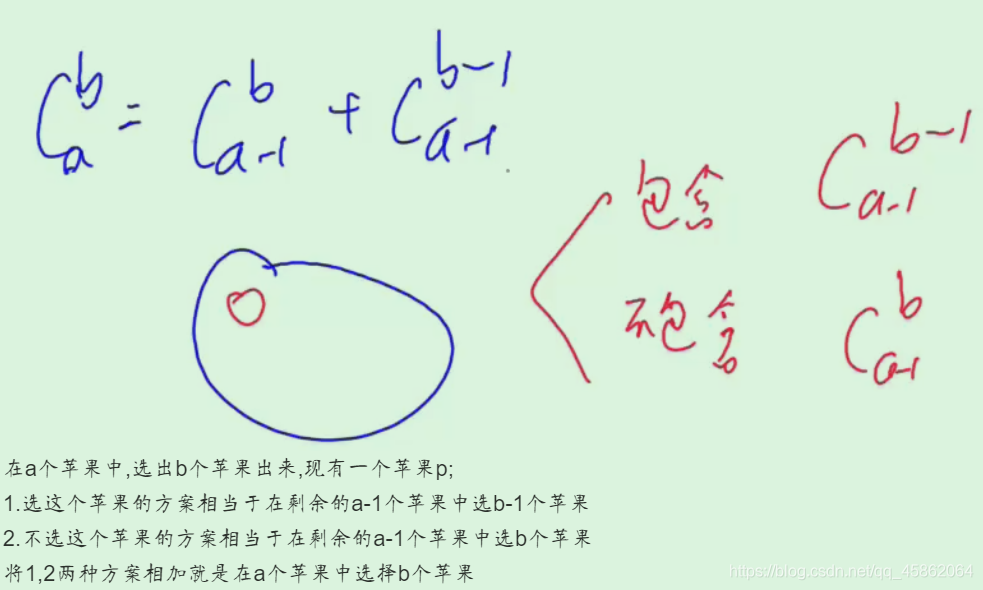
时间复杂度:O( N 2 N^2 N2)const int N = 2010, mod = 1e9 + 10;
typedef long long ll;
ll f[N][N];
void comb(void)
{for(int i = 0; i <= 2000; ++ i){for(int j = 0; j <= i; ++ j){if(!j) //初始化,第一列恒置为1f[i][j] = 1;else //递推公式f[i][j] = (f[i - 1][j] +f[i - 1][j - 1]) % mod;}}
}
2.预处理

由 C a b = a ! b ! ( a − b ) ! C_{a}^{b}=\frac{a!}{b!\left( a-b \right) !} Cab=b!(a−b)!a!
该公式求得组合数,而除法转换成求逆元;
时间复杂度:O( n l o g n nlogn nlogn)#include 3.卢卡斯定理

C a b ≡ C a % p b % p ∗ C a p b p ( m o d p ) C_{a}^{b}\equiv C_{a\%p}^{b\%p}*C_{\frac{a}{p}}^{\frac{b}{p}}\left( mod\,\,p \right) Cab≡Ca%pb%p∗Cpapb(modp)
组合数直接运算:
C a b = a ∗ ( a − 1 ) ∗ ⋅ ⋅ ⋅ ∗ ( a − b + 1 ) 1 ∗ 2 ∗ ⋅ ⋅ ⋅ ∗ b C_{a}^{b}=\frac{a*\left( a-1 \right) *···*\left( a-b+1 \right)}{1*2*···*b} Cab=1∗2∗⋅⋅⋅∗ba∗(a−1)∗⋅⋅⋅∗(a−b+1)
除法转换成对p的逆元;#include 4.高精度组合数
质因数分解+高精度
参考题解#include 5.卡特兰数
卡特兰数推导+题解
用逆元求组合数;#include 九、容斥原理
集合为奇则加,否则减;
精彩题解#include 十、博弈论
1.nim游戏
先手必胜状态:
a 1 ⊕ a 2 ⊕ a 3 ⊕ ⋅ ⋅ ⋅ ⊕ a n ≠ 0 a_1\oplus a_2\oplus a_3\oplus ···\oplus a_n\ne 0 a1⊕a2⊕a3⊕⋅⋅⋅⊕an=02.SG函数
重点是用代码模拟SG函数的第一部分,即遍历所有可选数字集合,并向下递归,最后mex操作找到未出现过的最小的自然数作为答案;
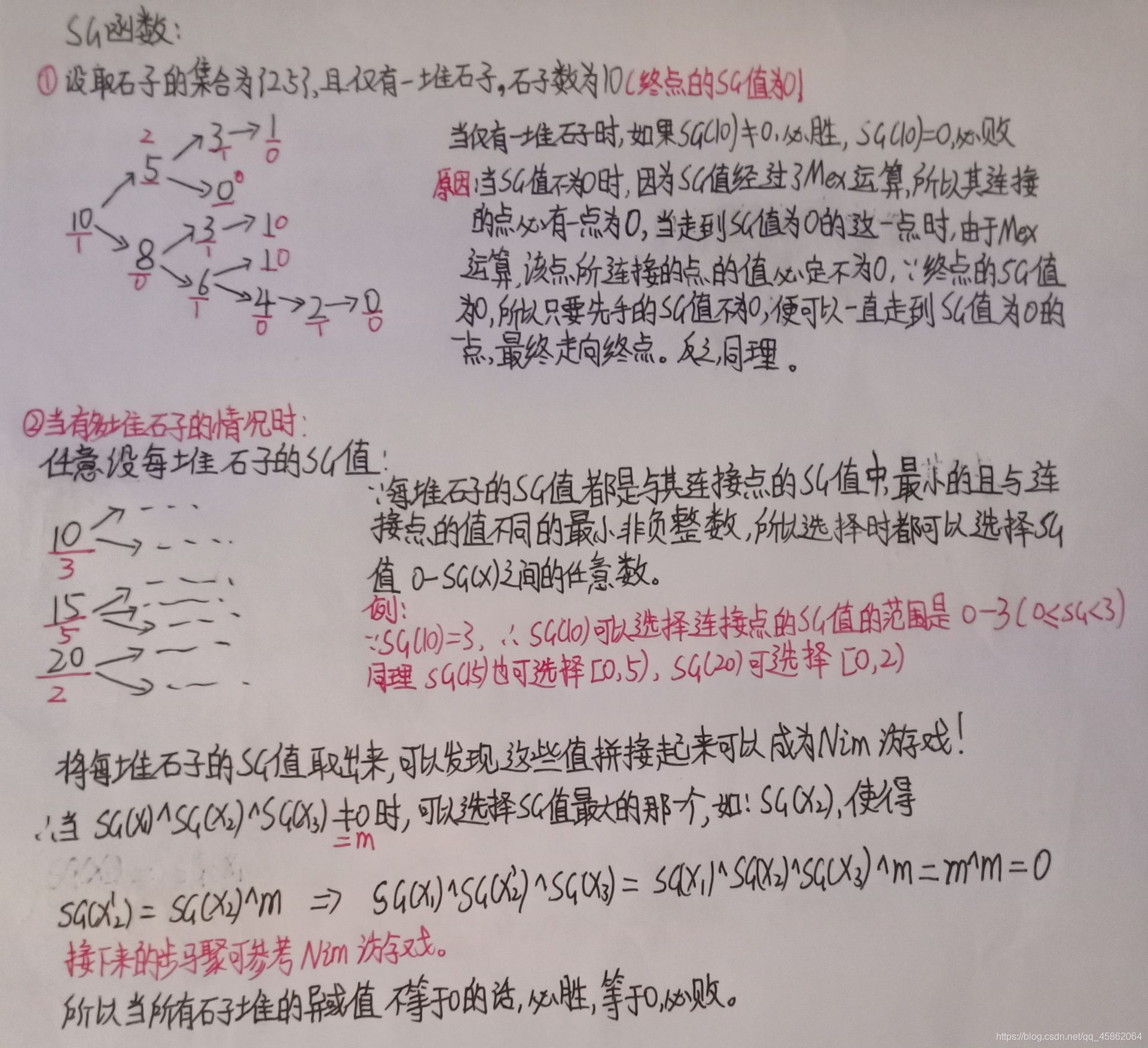
模板题#include 十一、有趣的数学
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!