史上最强数据结构----栈和队列相关笔试面试题

栈的队列相关笔试面试题

• 1. 栈和队列面试题
• • 1.1 括号匹配问题
  • 1.2 用队列实现栈
  • 1.3 用栈实现队列
  • 1.4 设计循环队列
• 2. 概念选择题
• 3. 栈和队列的用途

1. 栈和队列面试题

1.1 括号匹配问题

题目：

思路：

首先将所给的字符串进行遍历，如果是左括号就将它压入栈中，根据栈后进先出的特性，然后逐个取出栈中的左括号与后面剩下的右括号进行逐对进行匹配，如果不匹配就返回false，如果都匹配了就返回true。

例如：

代码：

typedef char STDataType;
typedef struct Stack
{STDataType* a;int top;//栈顶的位置int capacity;//容量
}ST;
void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->capacity = 0;ps->top = 0;
}
void StackDestory(ST*ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->capacity =ps->top =  0;
}
void StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity)//满了进行扩容{int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;ps->a = (STDataType*)realloc(ps->a,sizeof(STDataType)*newCapacity);if (ps->a == NULL){printf("fail malloc\n");exit(-1);}ps->capacity = newCapacity;}ps->a[ps->top++] = x;
}
void StackPop(ST* ps)
{assert(ps);assert(ps->top > 0);--ps->top;
}
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}
STDataType StackTop(ST* ps)
{assert(ps);assert(ps->top > 0);return ps->a[ps->top - 1];
}
int SizeStack(ST* ps)
{assert(ps);return ps->top;
}
//前面的所有代码就是定义一个栈以及栈的相关函数
bool isValid(char * s){ST st;StackInit(&st);while(*s){if(*s=='['||*s=='('||*s=='{'){StackPush(&st,*s);++s;}else{if(StackEmpty(&st))//当所给的字符串中只有右括号时直接返回false{StackDestory(&st);return false;}char top = StackTop(&st);//从栈中取一个左括号StackPop(&st);//进行出栈操作，让刚才取的字符出栈if((*s==']'&&top!='[')||(*s=='}'&&top!='{')||(*s==')'&&top!='('))//两个字符不相匹配的情况下直接返回false{StackDestory(&st);return false;}else{++s;}}}//栈为空，说明所有左括号都匹配了bool ret =  StackEmpty(&st);//判断是否只有左括号，如果只有左括号此时ret就为false，如果前面都已经匹配完了ret就等于trueStackDestory(&st);return ret;
}

1.2 用队列实现栈

解析上面的实例：

输入的第一行是执行的操作。第二行是执行操作的数据。

输出是对应的返回值。

思路：用两个队列实现栈。

栈的基本结构：

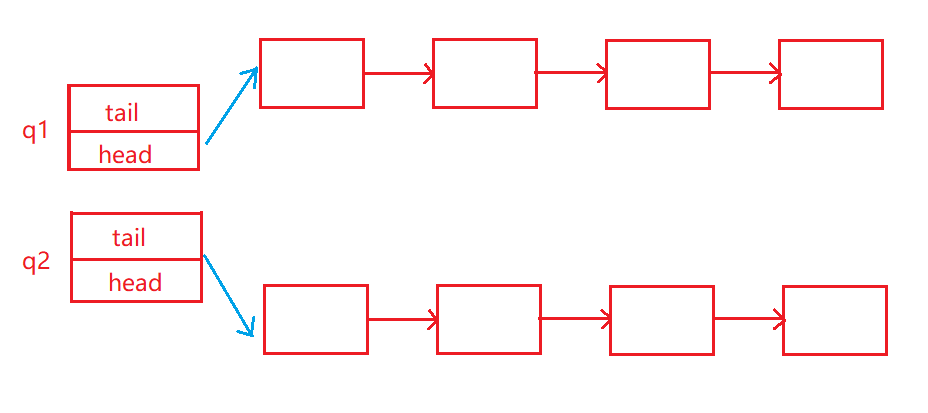
1、入栈，push数据到不为空的队列。

2、出栈，把不为空的队列的数据前N-1导入到另一个空队列，最后剩下的一个删掉。

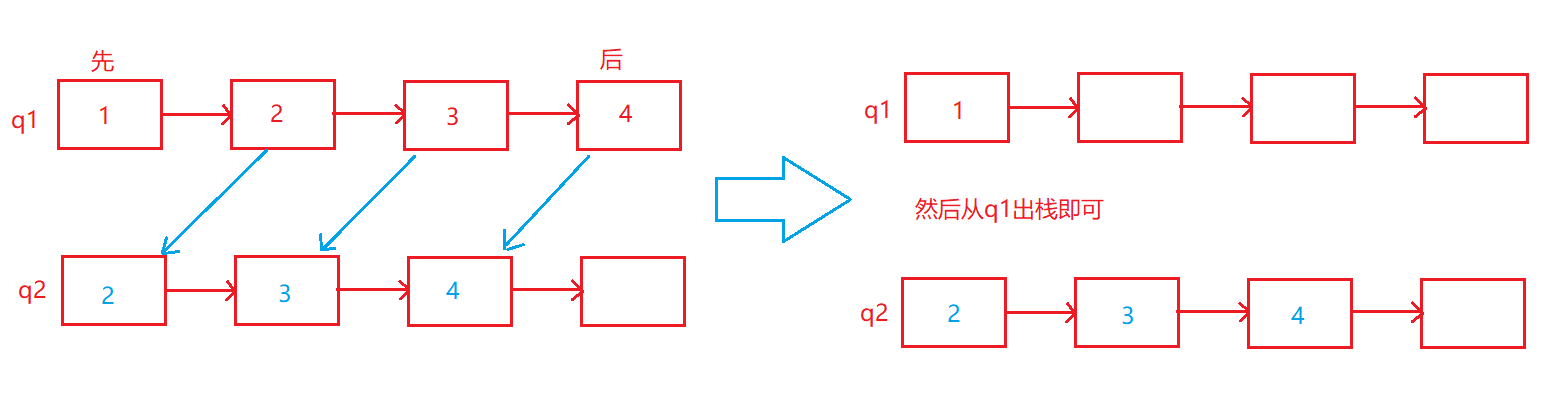
代码：

typedef int QDataType;
typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;
typedef struct Queue
{QNode* head;QNode* tail;
}Queue;
void QueueInit(Queue* pq);
void QueueDestory(Queue* pq);
void QueuePush(Queue*pq,QDataType x);
void QueuePop(Queue*pq);
size_t QueueSize(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
void QueueInit(Queue* pq)
{assert(pq);pq->head =pq->tail = NULL;
}
QNode* BuyQNode(QDataType x)
{QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){printf("fail malloc\n");exit(-1);}newnode->data = x;newnode->next = NULL;return newnode;
}
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = BuyQNode(x);if (pq->tail == NULL){assert(pq->head == NULL);pq->head= pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}}
void QueuePop(Queue* pq)
{assert(pq);assert(pq->tail&&pq->head);if (pq->head->next==NULL)//处理只有一个节点的时候{free(pq->tail);pq->tail = pq->head = NULL;}else//有多个节点{QNode* next = pq->head->next;free(pq->head);pq->head = next;}
}
size_t QueueSize(Queue* pq)
{assert(pq);size_t size = 0;QNode* cur = pq->head;while (cur!= pq->tail->next){size++;cur = cur->next;}return size;
}
QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->head);return pq->head->data;
}
QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->tail);return pq->tail->data;
}
void QueueDestory(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;
}
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head==NULL&&pq->tail==NULL;
}
typedef struct {Queue q1;Queue q2;
} MyStack;MyStack* myStackCreate() {MyStack* pst = (MyStack*)malloc(sizeof(MyStack));assert(pst);QueueInit(&pst->q1);//这一行代码和后面这一行代码等价:QueueInit(&(pst->q1));QueueInit(&pst->q2);//这一行代码和后面这一行代码等价:QueueInit(&(pst->q2));return pst;
}void myStackPush(MyStack* obj, int x) {assert(obj);if(!QueueEmpty(&obj->q1)){QueuePush(&obj->q1,x);}else{QueuePush(&obj->q2,x);}
}int myStackPop(MyStack* obj) {assert(obj);Queue *emptyQ = &obj->q1;Queue*nonEmptyQ = &obj->q2;if(!QueueEmpty(&obj->q1)){emptyQ = &obj->q2;nonEmptyQ = &obj->q1;}//把非空队列的前N个数据，导入空队列，剩下一个删掉//就实现了后进先出while(QueueSize(nonEmptyQ)>1){QueuePush(emptyQ,QueueFront(nonEmptyQ));//将非空队列的队头数据push到非空队列中QueuePop(nonEmptyQ);//将非空队列的队头数据出队}QDataType top = QueueFront(nonEmptyQ);QueuePop(nonEmptyQ);return top;
}int myStackTop(MyStack* obj) {assert(obj);if(!QueueEmpty(&obj->q1)){return QueueBack(&obj->q1);}else{return QueueBack(&obj->q2);}}
bool myStackEmpty(MyStack* obj) {assert(obj);return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}void myStackFree(MyStack* obj) {assert(obj);QueueDestory(&obj->q1);QueueDestory(&obj->q2);free(obj);
}

1.3 用栈实现队列

思路：

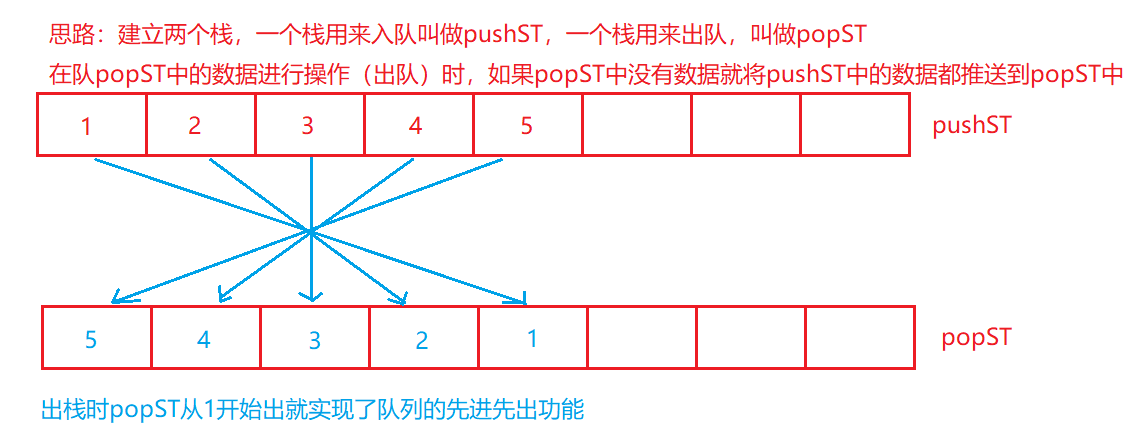
注意：在上面的代码中，在进行出队操作时，只要popST这个栈中有数据，那么我们就不进行倒数据的操作（即将push中的数据倒到popST这个栈中），只有当pop中的数据为空且我们要进行出队时才进行倒数据。

队列结构：

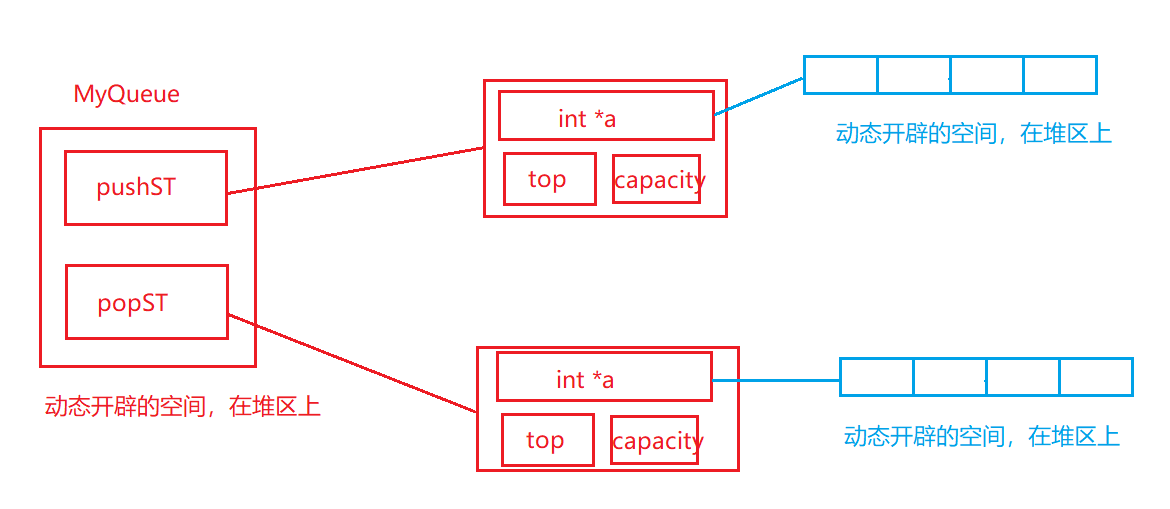
代码：

typedef int STDataType;
//数组栈的实现
typedef struct Stack
{STDataType* a;int top;//栈顶的位置int capacity;//容量
}ST;
void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->capacity = 0;ps->top = 0;
}
void StackDestory(ST*ps)
{assert(ps);free(ps->a);ps->a = NULL;ps->capacity =ps->top =  0;
}
void StackPush(ST* ps, STDataType x)
{assert(ps);if (ps->top == ps->capacity)//满了进行扩容{int newCapacity = ps->capacity == 0 ? 2 : 2 * ps->capacity;STDataType*new = (STDataType*)realloc(ps->a,sizeof(STDataType)*newCapacity);if (new == NULL){printf("fail malloc\n");exit(-1);}ps->a = new;ps->capacity = newCapacity;}ps->a[ps->top++] = x;
}
void StackPop(ST* ps)
{assert(ps);assert(ps->top > 0);--ps->top;
}
bool StackEmpty(ST* ps)
{assert(ps);return ps->top == 0;
}
STDataType StackTop(ST* ps)
{assert(ps);assert(ps->top > 0);return ps->a[ps->top - 1];
}
int SizeStack(ST* ps)
{assert(ps);return ps->top;
}
void StackInit(ST*ps);
void StackDestory(ST* ps);
void StackPush(ST* ps,STDataType x);
void StackPop(ST* ps);
bool StackEmpty(ST* ps);
int SizeStack(ST* ps);
STDataType StackTop(ST* ps);
typedef struct {ST pushST;ST popST;
} MyQueue;MyQueue* myQueueCreate() {MyQueue * myQueue = (MyQueue*)malloc(sizeof(MyQueue));assert(myQueue);StackInit(&myQueue->pushST);StackInit(&myQueue->popST);return myQueue;
}void myQueuePush(MyQueue* obj, int x) {assert(obj);StackPush(&obj->pushST,x);//入队直接向pushST插入即可
}int myQueuePop(MyQueue* obj){assert(obj);if(StackEmpty(&obj->popST))//push为空，就进行倒数据，就符合先进先出的顺序了{while(!StackEmpty(&obj->pushST)){StackPush(&obj->popST,StackTop(&obj->pushST));StackPop(&obj->pushST);}}STDataType ret = StackTop(&obj->popST);//临时保存返回的数据StackPop(&obj->popST);return ret;
}int myQueuePeek(MyQueue* obj) {assert(obj);if(StackEmpty(&obj->popST)){while(!StackEmpty(&obj->pushST)){StackPush(&obj->popST,StackTop(&obj->pushST));StackPop(&obj->pushST);}}return StackTop(&obj->popST);
}bool myQueueEmpty(MyQueue* obj) {assert(obj);return StackEmpty(&obj->pushST)&&StackEmpty(&obj->popST);
}void myQueueFree(MyQueue* obj) {assert(obj);StackDestory(&obj->pushST);StackDestory(&obj->popST);free(obj);
}

1.4 设计循环队列

为了避免空和满混淆，无法区分，多开一个空间。

1. front = tail时是空

2. tail下一个位置是front时是满

满的两种情况：

1、obj->tail = k && obj->head = 0

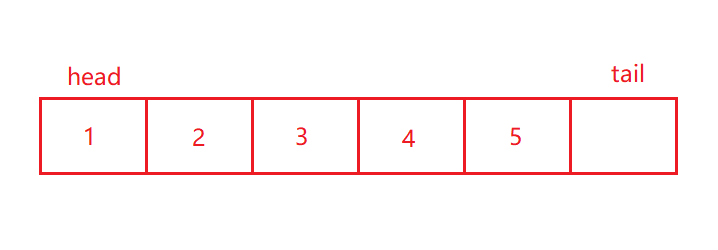
2、obj->tail+1 = obj->head

代码：

typedef struct {int *a;int head;//循环队列的头int tail;//循环队列的尾int capacity;//循环队列元素的最大数目
} MyCircularQueue;bool myCircularQueueIsEmpty(MyCircularQueue* obj);//判断循环队列是否为空的声明
bool myCircularQueueIsFull(MyCircularQueue* obj);//判断循环队列是否为满的声明
MyCircularQueue* myCircularQueueCreate(int k) //循环队列的初始化
{MyCircularQueue*myCircularQ = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));assert(myCircularQ);int *tmp = (int*)malloc(sizeof(int)*(k+1));assert(tmp);myCircularQ->a = tmp;myCircularQ->head = 0;myCircularQ->tail = 0;myCircularQ->capacity = k;return myCircularQ;
}bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) //向循环队列插入一个元素，如果成功插入则返回真。
{assert(obj);if(myCircularQueueIsFull(obj))//满了的情况{return false;}obj->a[obj->tail] = value;if(obj->tail==obj->capacity)//此时已经到达了开辟数组的最后一个位置，tail再进行++操作后会跳跃到第一个位置{obj->tail = 0;}else{++obj->tail;}return true;
}bool myCircularQueueDeQueue(MyCircularQueue* obj) //从循环队列中删除一个元素，如果成功删除则返回真。
{assert(obj);if(myCircularQueueIsEmpty(obj))//循环队列中为空的情况{return false;}if(obj->head==obj->capacity)//循环队列中的head在开辟的最后的一个空间位置的情况，head要发生跳跃{obj->head = 0;}else{++obj->head;}return true;
}int myCircularQueueFront(MyCircularQueue* obj) //从队首获取元素，如果队列为空，返回 -1 。
{assert(obj);if(myCircularQueueIsEmpty(obj))//队列元素为空的情况return -1;return obj->a[obj->head];
}int myCircularQueueRear(MyCircularQueue* obj)//获取队尾元素，如果队列为空，返回 -1 。
{assert(obj);if(myCircularQueueIsEmpty(obj))//循环队列元素为空的情况return -1;if(obj->tail==0)//尾在头的时候，就要返回最后一个空间的位置{return obj->a[obj->capacity];}else{return obj->a[obj->tail-1];//正常情况返回tail的前一个位置}
}bool myCircularQueueIsEmpty(MyCircularQueue* obj) //判断循环队列是否满
{assert(obj);return obj->tail==obj->head;//尾下标等于头下标的时候就是空
}bool myCircularQueueIsFull(MyCircularQueue* obj) //判断循环队列是否满
{assert(obj);if(obj->tail==obj->capacity && obj->head==0)//判断的是尾下标指向最后一块空间，头下标在最靠前的空间{return true;}else{return obj->tail+1 ==obj->head;}
}  void myCircularQueueFree(MyCircularQueue* obj) //循环队列的销毁
{assert(obj);free(obj->a);free(obj);
}

2. 概念选择题

1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出 栈的顺序是（B）。

A 12345ABCDE

B EDCBA54321

C ABCDE12345

D 54321EDCBA

2.若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（C）

A 1,4,3,2

B 2,3,4,1

C 3,1,4,2

D 3,4,2,1

解析：C选项中，3出来之后要想出1的话，就必须先出2。

3.循环队列的存储空间为 Q(1:100) ，初始状态为 front=rear=100 。经过一系列正常的入队与退队操作 后， front=rear=99 ，则循环队列中的元素个数为（ D）

A 1

B 2

C 99

D 0

解析：由前面循环队列的实现，很容易就得知此时元素的个数为0。

4.以下( )不是队列的基本运算？ （B）

A 从队尾插入一个新元素

B 从队列中删除第i个元素

C 判断一个队列是否为空

D 读取队头元素的值

5.现有一循环队列，其队头指针为front，队尾指针为rear；循环队列长度为N，实际最多存储N - 1个数据。其队内有效长度为（B）(假设队头不存放数据)

A (rear - front + N) % N + 1

B (rear - front + N) % N

C ear - front) % (N + 1)

D (rear - front + N) % (N - 1)

解析：此题要考虑两种情况：

第一种情况：front在rear的前面

第二种情况：front在rear的后面

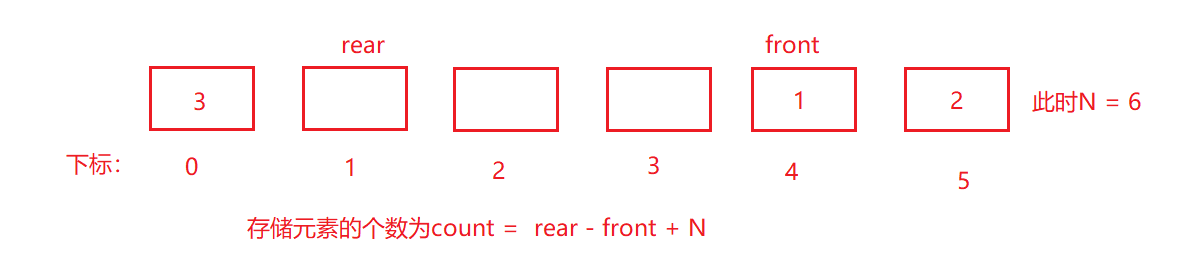
注意：从最后绕到了最前面其实就相当于在最后面越界继续相加！如下图所示：

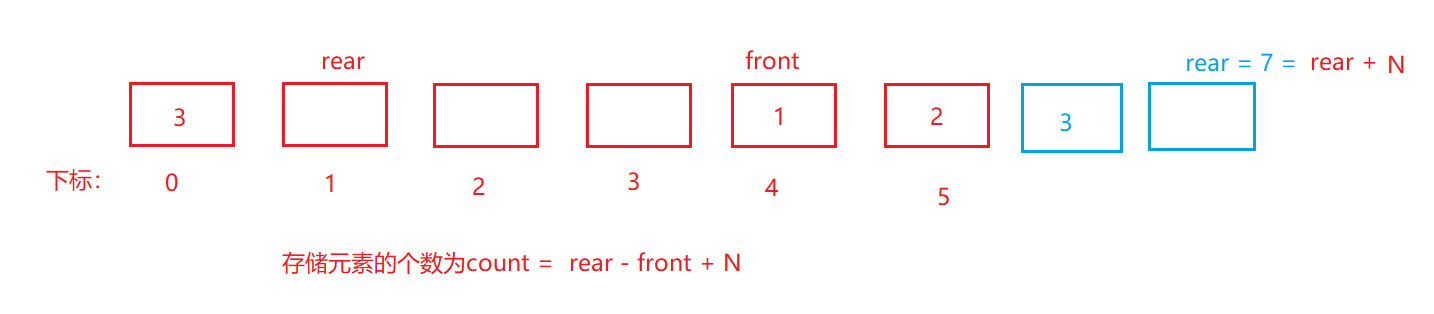
综合上面两种情况：最终公式为：

count = (rear - front + N ) % N （为什么第一种也加了N？因为对于front在rear前面的情况来说，是否加N对结果没有任何的影响，因为还要对N进行取模操作）

3. 栈和队列的用途

栈：用来解决括号匹配，逆波兰表达式的求解，递归改非递归等等。

队列：公平排队，广度优先遍历等等。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！