2022牛客暑期多校训练营1（ACDGIJ）

题集链接；

文字题解、视频题解；

目录：

• • A Villages: Landlines
  • • • 思路
      • 代码
  • C Grab the Seat!
  • • • 思路
      • 代码
  • D Mocha and Railgun
  • • • 思路
      • 代码
  • G Lexicographical Maximum
  • • • 思路
      • 代码
  • I Chiitoitsu
  • • • 思路
      • 代码
  • J Serval and Essay
  • • • 思路
      • 代码
  • ED

A Villages: Landlines

区间和并

思路

一维线上有若干个建筑物，每个建筑物有自己的覆盖范围，问所有建筑物间空白区域长度（题目描述有些复杂了）；

每个建筑物对应了一段区间，求出合并后区间间的长度即可；

代码

#include 
using namespace std;
typedef long long ll;
pair<ll, ll> ps[200005];
int main()
{int n;ll p, q;cin >> n;for (int i = 1; i <= n; i++){scanf("%lld%lld", &p, &q);ps[i].first = p - q, ps[i].second = p + q;}sort(ps + 1, ps + n + 1);ll l, r, ans = 0;l = ps[1].first, r = ps[1].second;for (int i = 2; i <= n; i++){if (ps[i].first <= r)r = max(ps[i].second, r);else{ans += ps[i].first - r;l = ps[i].first, r = ps[i].second;}}cout << ans;return 0;
}

C Grab the Seat!

计算几何（？）

思路

文字描述比较繁琐~
以样例2的第一次变化为例：

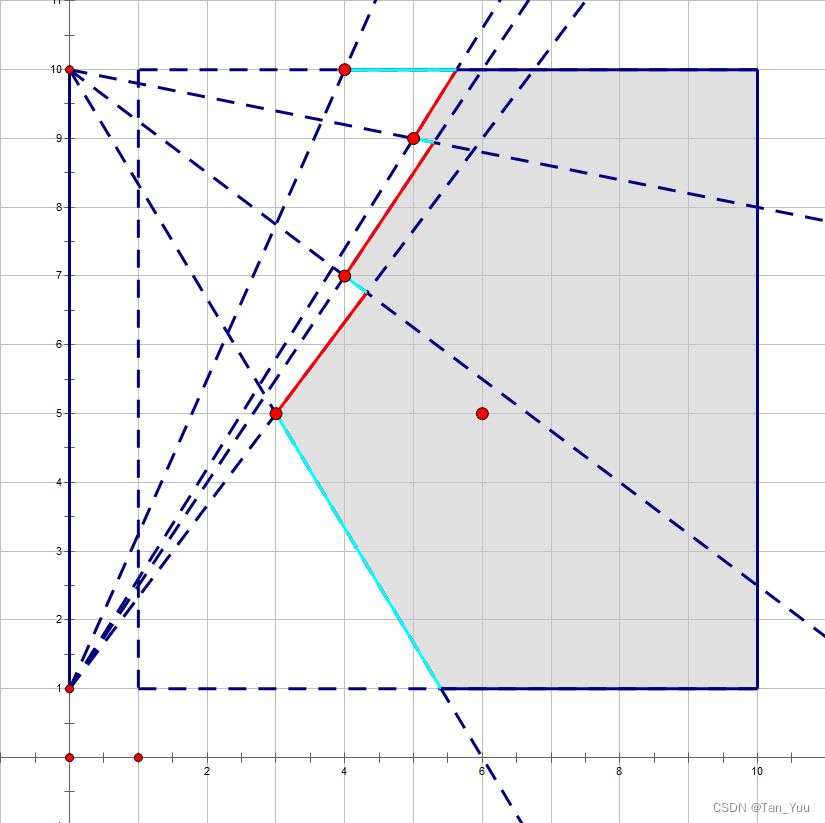
我们可以观察到，灰色区域的所有点（含边界）都不是好点，而影响灰色边界范围的，仅是每一行最靠前的一个有人位；

我们将灰色区域的“可变边界”（由有人位贡献的边界）划分成红色和青色两部分，然后可以通过从下至上和从上至下两次遍历维护每行的好点数；

对于每次遍历，我们只需要记录已遍历部分中斜率最大/最小的边界线，由其与此行的交点坐标限定此行的好点数。在维护边界线时，注意边界情况（斜率为0）；

两次遍历后，累加每行的好点数即可得到答案，每次查询的时间复杂度为$O(n)$；

代码

#include 
using namespace std;
typedef long long ll;
typedef long double ld;
const ll M = 1e9 + 7;
const double eps = 1e-6;
pair<int, int> p[200005];
set<int> lne[200005];
ll bar[200005];
ll cnt(int n, int m)
{int mnl = n + 1, mxl = 0;for (int i = 1; i <= m; i++){bar[i] = n;if (!lne[i].empty())mnl = min(mnl, i), mxl = max(mxl, i);}pair<double, double> now = {1, 0};for (int i = 1; i <= m; i++){if (!lne[i].empty()){pair<double, double> tmp = {(double)*lne[i].begin(), (double)i};if ((tmp.second - 1) / tmp.first > (now.second - 1) / now.first)now = tmp;}ll lim = n;if (fabs(now.second) > eps) //边界点有效{if (fabs(now.second - 1) > eps) //边界点不临边lim = (i - 1.0) * now.first / (now.second - 1) - eps;else if (i == 1) //边界点临边且该行为边{lim = now.first - 1 + eps;}bar[i] = min(bar[i], lim);}// printf("\\%d\n", bar[i]);}now = {1, m + 1};for (int i = m; i >= 1; i--){if (!lne[i].empty()){pair<double, double> tmp = {(double)*lne[i].begin(), (double)i};if ((tmp.second - m) / tmp.first < (now.second - m) / now.first)now = tmp;}ll lim = n;if (fabs(now.second - m - 1) > eps) //边界点有效{if (fabs(now.second - m) > eps) //边界点不临边lim = (i - m) * now.first / (now.second - m) - eps;else if (i == m) //边界点临边且该行为边{lim = now.first - 1 + eps;}bar[i] = min(bar[i], lim);}}ll ans = 0;for (int i = 1; i <= m; i++){// printf("*%d\n", bar[i]);ans += bar[i];}return ans;
}
int main()
{int n, m, k, q;cin >> n >> m >> k >> q;for (int i = 1; i <= k; i++){scanf("%d%d", &p[i].first, &p[i].second);}for (int i = 1; i <= k; i++){lne[p[i].second].insert(p[i].first);}while (q--){pair<int, int> tmp;int cg;scanf("%d%d%d", &cg, &tmp.first, &tmp.second);lne[p[cg].second].erase(p[cg].first);p[cg] = tmp;lne[tmp.second].insert(tmp.first);printf("%lld\n", cnt(n, m));}return 0;
}

D Mocha and Railgun

计算几何

思路

有一个以原点为圆心，半径给定的圆，圆内给定一个点Q和长度d，以Q为中点，2d为长度在圆内构造线段（数据保证线段一定不会出圆），问能够投影在线段某一侧（无所谓）的圆周最大长度；

不难想象（没有进行证明），在线段方向为径向时，题求长度最长；

代码

#include 
using namespace std;
typedef long long ll;
typedef long double ld;
const ld eps = 1e-12;
const ld PI = acos(-1.0);
int sign(ld x)
{if (fabs(x) < eps)return 0;if (x > 0)return 1;elsereturn -1;
}
int main()
{int t;cin >> t;while (t--){ld r, x, y, d, dis1, dis2;scanf("%Lf%Lf%Lf%Lf", &r, &x, &y, &d);double disq = sqrt(x * x + y * y);dis1 = disq - d;dis2 = disq + d;ld ac1, ac2;ac1 = acos(dis1 / r);ac2 = acos(dis2 / r);printf("%.12Lf\n", (ac1 - ac2) * r);}return 0;
}

G Lexicographical Maximum

贪心

思路

给定一个数字，求小于等于它的数字中，字典序最大的数字；

贪心策略：如果该数满足除最后一位外都为9，则输出该数。否则输出相比此数少一位的9；

代码

#include 
using namespace std;int main()
{string s;cin >> s;bool f = true;for (int i = 0; i != s.length() - 1; i++){if (s[i] != '9'){f = false;break;}}if (f)cout << s << '\n';elsefor (int i = 0; i != s.length() - 1; i++){cout << 9;}return 0;
}

I Chiitoitsu

概率期望

思路

一副牌有34种牌，每种四张，在排队中给出13张初始手牌，保证初始手牌中相同的牌不超过两张；

每轮做如下操作：

1. 在牌堆中随机抽出一张牌，加入手牌；
2. 如果手牌中满足有不同种类的7对相同牌（11，33，22，77，99……）则结束游戏；
3. 否则弃掉一张牌，保持13张手牌；

给出初始手牌，问最优（最快结束）策略下结束游戏的轮数期望；

对于给定两个参数：牌堆剩余牌数l & 待配对牌数n，对于所有l,n相同的情况，此时到游戏结束的轮数期望也相同；

我们定义给定l,n的轮数期望为 $f(l,n)$ ，则有递归式：
f ( l , n ) = 1 + { 3 n l f ( l − 1 , n − 2 ) if  n > 1 0 else + { l − 3 n l f ( l − 1 , n ) if  l > 3 n 0 else f(l,n)=1+\begin{cases} \frac{3n}{l}f(l-1,n-2)&\text{if }n>1\\ 0&\text{else} \end{cases}+ \begin{cases} \frac{l-3n}{l}f(l-1,n)&\text{if }l>3n\\ 0&\text{else} \end{cases} f(l,n)=1+{l3n​f(l−1,n−2)0​if n>1else​+{ll−3n​f(l−1,n)0​if l>3nelse​
直观来说，前面的cases描述的是抽到待配对牌中的一张，后面的cases描述的是没有抽到；

记忆化存储 $f(l,n)$ 的值即可；

代码

#include 
using namespace std;
typedef long long ll;
typedef long double ld;
const ll M = 1e9 + 7;
ll qm(ll a, ll b = M - 2)
{ll ans = 1;for (; b; b >>= 1){if (b & 1)ans = ans * a % M;a = a * a % M;}return ans;
}
ll tab[150][14];
ll f(ll lft, ll ndd)
{if (tab[lft][ndd])return tab[lft][ndd];ll ans = 1;if (ndd > 1)ans += 3 * ndd * qm(lft) % M * f(lft - 1, ndd - 2) % M;if (lft > 3 * ndd)ans += (lft - 3*ndd) * qm(lft) % M * f(lft - 1, ndd) % M;ans %= M;return tab[lft][ndd] = ans;
}
int main()
{int t,tt=1;cin >> t;while (t--){string g;int cnt = 0;map<string, int> mp;cin >> g;for (int i = 0; g[i]; i += 2){mp[g.substr(i, 2)]++;if (mp[g.substr(i, 2)] == 2)cnt++;}printf("Case #%d: %lld\n", tt++, f(123, 13 - 2 * cnt));}return 0;
}

J Serval and Essay

拓扑排序 并查集

思路

给出一个无重边自环的有向图，选定某一点作为起点，以拓扑排序的逻辑进行扩展，求出扩展后点数最大值；

拓扑排序优化失败，之后并查集暴力过；

代码

#include 
using namespace std;
typedef long long ll;
typedef long double ld;
const ll M = 1e9 + 7;
const double eps = 1e-6;vector<int> rod[200005];
int cnt[200005];//cnt实际无意义
pair<int, int> bel[200005];
int ord[200005];
inline int read()
{int v = 0, c = 1;char ch = getchar();while (!isdigit(ch)){if (ch == '-')c = -1;ch = getchar();}while (isdigit(ch)){v = v * 10 + ch - 48;ch = getchar();}return v * c;
}
int find(int x)
{if (bel[x].first == x)return x;elsereturn bel[x].first = find(bel[x].first);
}
bool check(int x)
{if (find(x) != x || rod[x].empty()) //如果该点不独立或这个点没有父节点return false;int now = find(rod[x][0]);for (auto v : rod[x]) //判断是否所有父节点都在一个集合里{if (now != find(v))return false;}if (now == x) //判断父节点是否与自己在一个集合return false;return true;
}
int main()
{int t, n, k, q, tt = 1;cin >> t;while (t--){scanf("%d", &n);for (int i = 1; i <= n; i++)rod[i].clear(), bel[i] = {i, 1};for (int i = 1; i <= n; i++){// scanf("%d", &cnt[i]);cnt[i] = read();for (int j = 1; j <= cnt[i]; j++){q = read();rod[i].push_back(q);}}for (int i = 1; i <= n; i++){ord[i] = i;}// random_shuffle(ord + 1, ord + n + 1);随机化后会超时int ans = 1;while (1){// printf("*");int flag = 0;for (int i = 1; i <= n; i++){int nw = ord[i];if (check(nw)) //判断这个点能否进行合并{flag = 1;int f = find(rod[nw][0]);bel[nw].first = f;bel[f].second += bel[nw].second;ans=max(bel[f].second,ans);}}if (!flag) //如果所有点都不能进行合并，结束break;}// for (int i = 1; i <= n; i++)//     ans = max(ans, bel[i].second);printf("Case #%d: %d\n", tt++, ans);}return 0;
}
//参考https://ac.nowcoder.com/acm/contest/view-submission?submissionId=52793209

ED

1. 该学数学了，不然H补不了；
2. 这场题解不太好写，也许和我太长时间没写题解有关系；
3. 14159；

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！