单层感知器介绍

单层感知器介绍

一、单层感知器介绍

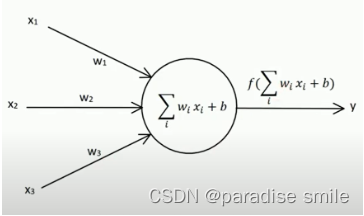
输入节点：x1,x2,x3

输出因子：y

权向量：w1,w2,w3

偏置因子：b

激活函数：
s i g n ( x ) = { 1 x ≥ 0 − 1 x ≤ 0 sign(x) = \begin{cases} 1 \quad x \geq 0 \\ -1 \quad x \leq 0 \end{cases} sign(x)={1x≥0−1x≤0​

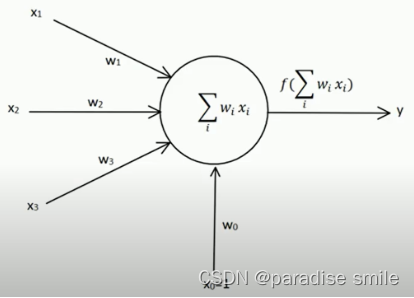
二、感知器的学习规则

y = f ( ∑ i = 1 m x i w i ) y = f(\sum_{i=1}^{m}x_iw_i) y=f(i=1∑m​xi​wi​)
i=0,1,2…y是网络输出 f是sign函数
Δ w i = η ( t − y ) x i \Delta w_i = \eta(t-y)x_i Δwi​=η(t−y)xi​
η表示学习率

t表示正确的标签

t和y的取值为正负1
Δ w i = ± 2 η x i \Delta w_i = \pm 2\eta x_i Δwi​=±2ηxi​

w i = w i + Δ w i w_i = w_i + \Delta w_i wi​=wi​+Δwi​

示例：

假设： t = 1 , η = 1 , x 1 = 1 , w 1 = − 5 , b = 0 s t e p 1 : y = s i g n ( 1 ∗ ( − 5 ) ) = − 1 Δ w = 1 ∗ ( 1 − ( − 1 ) ) ∗ 1 = 2 w 1 = w 1 + Δ w = − 3 s t e p 2 : y = s i g n ( 1 ∗ ( − 3 ) ) = − 1 Δ w = 1 ∗ ( 1 − ( − 1 ) ) ∗ 1 = 2 w 1 = w 1 + Δ w = − 1 s t e p 3 : y = s i g n ( 1 ∗ ( − 1 ) ) = − 1 Δ w = 1 ∗ ( 1 − ( − 1 ) ) = 2 w 1 = w 1 + Δ w = 1 y = s i g n ( 1 ∗ 1 ) = 1 = t 假设：t=1,\eta=1,x_1=1,w_1=-5,b=0 \\ \\ step1: y = sign(1*(-5)) = -1 \\ \Delta w = 1*(1-(-1))*1 = 2 \\ w1 = w1 + \Delta w = -3 \\ \\ step2:y = sign(1*(-3)) = -1 \\ \Delta w = 1*(1-(-1)) * 1 =2 \\ w1 = w1 + \Delta w = -1\\ \\ step3:y = sign(1*(-1)) = -1 \\ \Delta w = 1*(1-(-1)) = 2 \\ w1 = w1 + \Delta w = 1\\ y = sign(1*1) = 1 = t 假设：t=1,η=1,x1​=1,w1​=−5,b=0step1:y=sign(1∗(−5))=−1Δw=1∗(1−(−1))∗1=2w1=w1+Δw=−3step2:y=sign(1∗(−3))=−1Δw=1∗(1−(−1))∗1=2w1=w1+Δw=−1step3:y=sign(1∗(−1))=−1Δw=1∗(1−(−1))=2w1=w1+Δw=1y=sign(1∗1)=1=t

三、模型收敛条件

1.误差小于某个预先设定的较小的值

2.两次迭代之间的权值变化已经很小

3.设定最大迭代次数，当迭代次数超过最大次数就停止

四、单层感知器程序

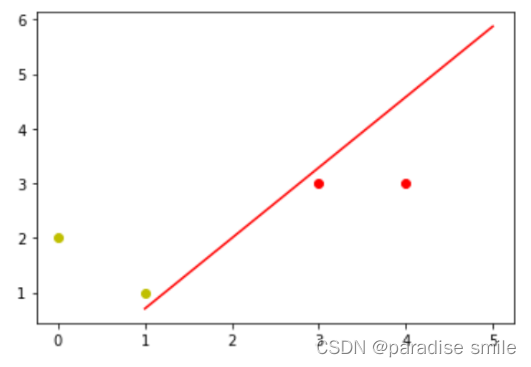
题目：假设平面坐标系上有四个点，(3,3),(4,3)这两个点的标签为1，(1,1),(0,2)这两个点的标签为-1。构建神经网络来分类。

思路：我们要分类的数据是2维数据，所以只需要2个输入节点，我们可以把神经元的偏置值也设置成一个节点，这样我们需要3个输入节点。

输入数据有4个(1,3,3),(1,4,3),(1,1,1),(1,0,2)，数据对应的标签为(1,1,-1,-1)

初始化权值w0 ,w1 ,w2取-1到1的随机数

学习率(learning rate)设置为0.11

激活函数为sign函数

#导入包
import numpy as np
import matplotlib.pyplot as plt

#导入数据
x_data = np.array([[1, 3, 3],[1, 4, 3],[1, 1, 1],[1, 0, 2]])
#标签
y_data = np.array([[1], [1],[-1],[-1]])
#初始化w
w = (np.random.random([3, 1]) - 0.5) * 2learning_rate = 0.11
net = 0# 更新函数def update():global x_data, y_data, w, learning_data, net# 预测值predict_value = np.sign(np.dot(x_data, w))Delta_w = learning_rate * x_data.T.dot(y_data - predict_value)w = w + Delta_wfor i in range(100):update()print(w)print(i)net = np.sign(x_data.dot(w))print(net)if (net == y_data).all():print('Finish')print(i)break# 导入数据画图# 正样本x_1 = [3, 4]
y_1 = [3, 3]# 负样本x_2 = [1, 0]
y_2 = [1, 2]#截距k
k = -w[1] / w[2]
b = -w[0] / w[2]
print('k=', k)
print('b=',b)xdata = (1, 5)
plt.scatter(x_1, y_1,c='r')
plt.scatter(x_2, y_2, c='y')
plt.plot(xdata, k*xdata+b, 'r-')
plt.show()

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！