矩阵于线性代数

矩阵于线性代数

虽然从本科开始就接触了线性代数，对于矩阵的理解却一直停留在书本的习题上，以至于后来很多跟矩阵相关的数学概念都没有能及时领悟。所以我想通过这篇文章对我再次学习矩阵的理解进行总结。个人觉得西方人对于矩阵的理解还是相对更好一些，因为教学更偏向于去理解如何将问题向量化，然后在用MATLAB或者PYTHON去计算结果。矩阵和向量在当今的大数据时代也更为重要。希望之后有时间可以把接下来学习过程中矩阵的应用分享到这里。

注：很多知识都来自于互联网（我不生产知识，我只是知识的搬运工），此篇博文参考Youtube 3b1b，B站也有熟肉。

向量

提到矩阵，首先要回顾的就是向量。只是向量在不止一门学科里被提及到：物理的向量指的是一个箭头，有长度，有方向，可以在摆放在空间的任意位置（1a）；计算机里的向量更像是一个列表（1b）。而我们这里的向量是一个有方向，有大小，但是起源于原点的箭头（1c）。

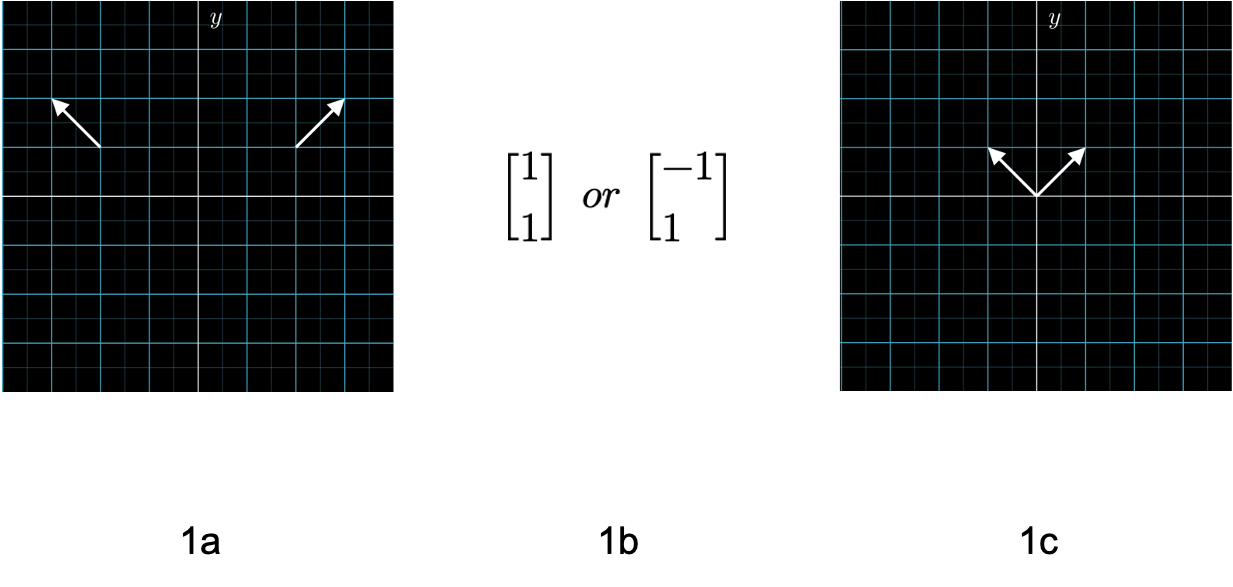
关于向量的运算这里不再赘述。

矩阵与线性变换

矩阵是什么？怎么去理解矩阵乘以向量？怎么去理解矩阵乘以矩阵？

线性代数的核心应该就是线性变换吧，变换指的是坐标的变换，而坐标系就是可以用矩阵来表示的（用列向量来表示坐标系的单位向量）。线性，简单来说，就是任意一条直线，变换后依旧保持直线或变成一个点（降维）。另外还有一个重要的特征，原点不变。

比方说我们常见的XY坐标系就是：

假设坐标系中有两个向量（，）和（，），如果我们现在希望变换到另一个坐标系，比方说UV：

这两个向量在UV坐标系中是（，）和（，），但是基于我们原先的XY坐标系却是（，）和（，）：

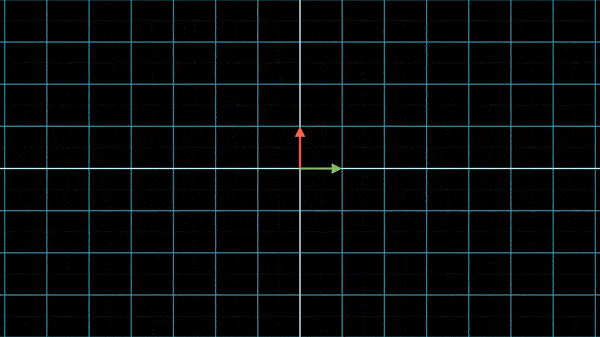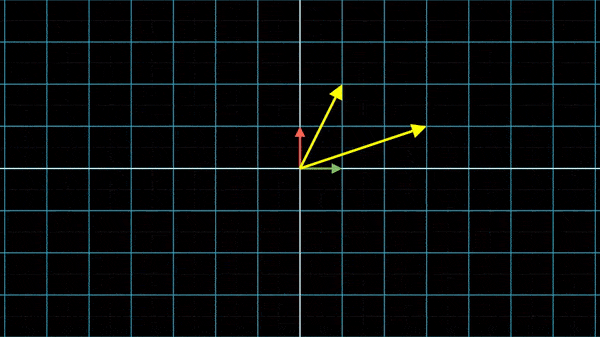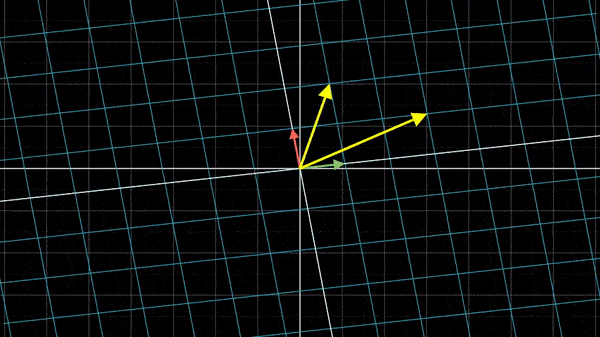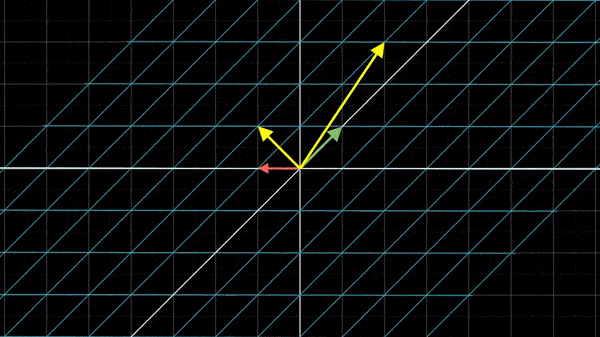
所以矩阵乘以向量，其实是将该矩阵所表示的坐标系中的向量翻译到XY坐标系中：

,

.

然而，刚刚那个UV坐标系可以通过两次变换得到（先，再）：

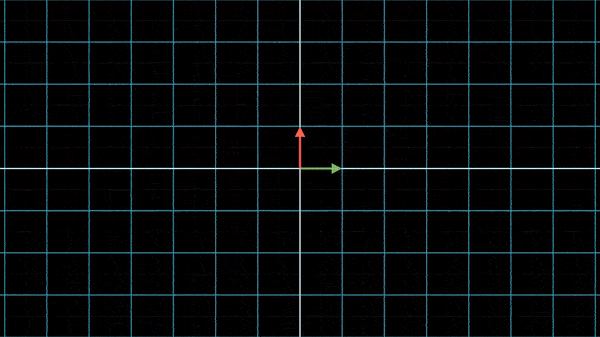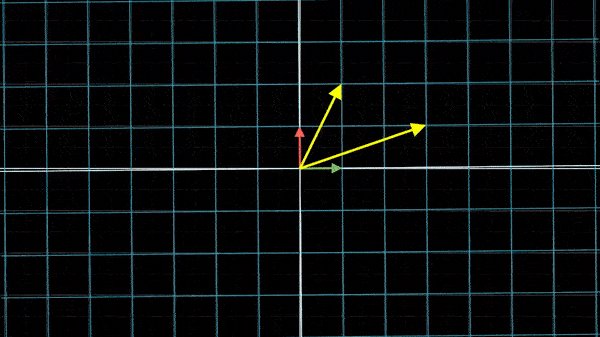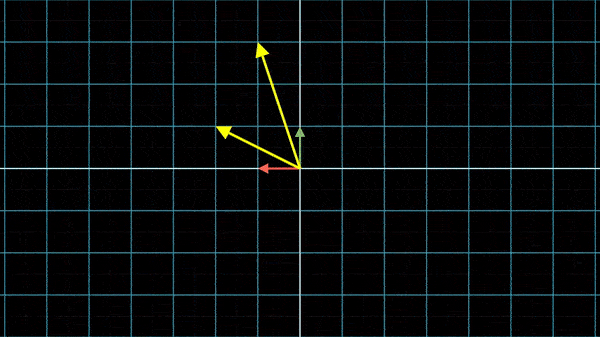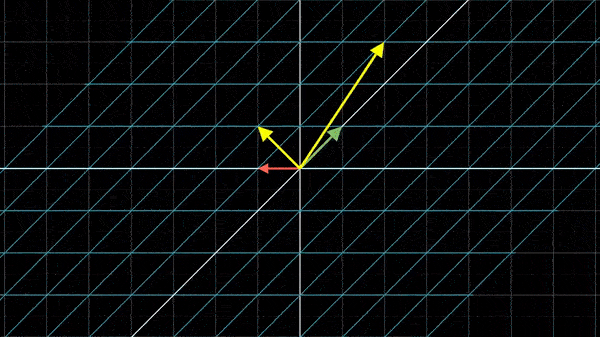
所以矩阵乘以矩阵其实就是对XY坐标系先变换一次得到了新的基向量，再对XY坐标系变换一次，观察新的基向量落于什么位置。但是变换的顺序是不可以更换的。假如我们刚刚是先应用，再应用，结果会是（）：

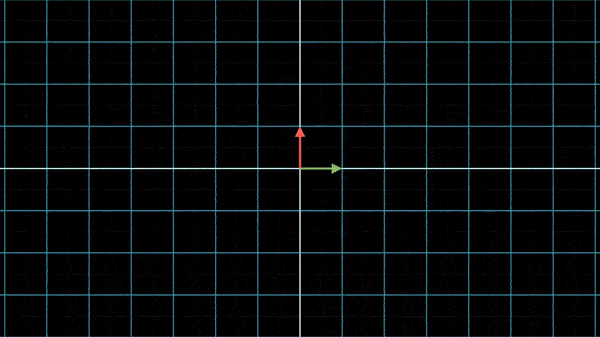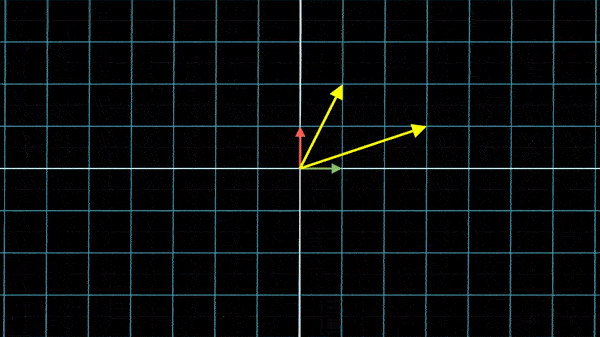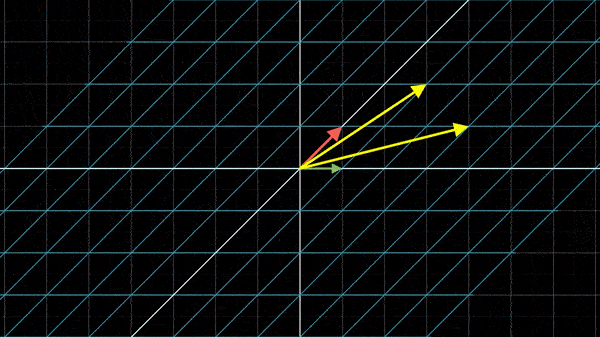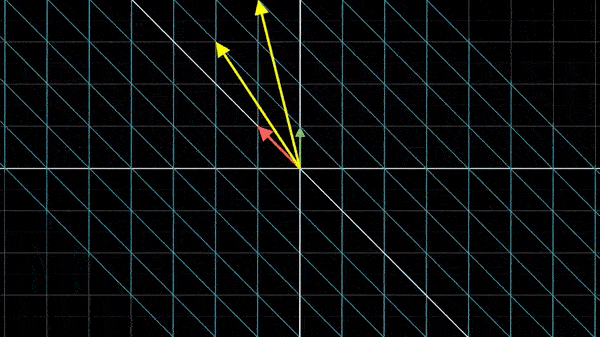
矩阵相关概念

秩

矩阵的秩是什么？假设矩阵A为：

,

根据书本我们可以计算如下：

.

那么，4 又是什么呢？这让我想起了《琅琊榜》中霓凰与林殊相认的场景：所有人都在问苏哲是谁，当发现他是梅长苏后，只有霓凰会继续追查，梅长苏又是谁。

前面提到了，矩阵其实就是将XY坐标系换到另一个坐标系。所以A矩阵就是将原先的标准XY基向量变成：

矩阵的秩动态示意图

从视频中可以看出，我们算出来的4其实是基向量所表示的四边形面积的变化。当然，这个面积的变化不是仅仅针对这个四边形，是所有的形状的面积都会相应的变化：

线性变换后的图形面积

如果我们再根据矩阵B变换一次：

矩阵相乘后得到的秩

我们可以看到，被A矩阵放大的四边形面积被B矩阵再次放大。我们也可以看出：

.

当然，秩可以是负数，意味着坐标系被翻转了；也可以是0，意味着新的基向量线性相关，在一条线上（从二维降到了一维）。

逆矩阵

刚刚的A矩阵将基向量从标准XY基向量变成，那么什么样的变换可以在变换标准XY基向量的同时，将再变回到之前的基向量。这里就引入了逆矩阵：

逆矩阵的动态演示

如果A的秩是0的话，无论你如何再次线性变换基向量，也没办法让新的基向量回到之前的基向量，也就是不存在逆矩阵。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！