【Matlab】三维曲线与三维曲面

三维曲线与三维曲面

三维曲线

plot3函数

plot3(x, y, z)：

1. x、y、z为同型向量时，每一个位置的(x, y, z)组成一个点的坐标。
2. x、y、z为同型矩阵时，每一列对应一条曲线，因此，x（或y或z）的列数为绘制出的曲线条数。
3. x、y、z中有矩阵有向量时，若向量为行向量，则应与矩阵的列数相同；若向量为列向量，则应与矩阵的行数相同。

plot3(x1, y1, z1, 选项, x2, y2, z2, 选项, ……)：同时绘制多条曲线。

t=0:0.01:2*pi;
t=t';
x=[t t t t t];
y=[sin(t) sin(t)+1 sin(t)+2 sin(t)+3 sin(t)+4];
z=[t t t t t];
subplot(121)
plot3(x, y, z)
grid ont=0:0.01:2*pi;
x=t;
y=[sin(t); sin(t)+1; sin(t)+2; sin(t)+3; sin(t)+4];
z=t;
subplot(122)
plot3 (x, y, z)
grid on

fplot3函数

fplot3(funx, funy, funz, tlims, 选项)：funx、funy、funz代表定义曲线x、y、z坐标的函数，通常采用函数句柄的形式。tlims为参数函数自变量的取值范围，用二元向量[tmin，tmax]描述，默认为[-5，5]。用于绘制参数方程曲线。

xt = @(t) exp(-t/ 10).*sin(5*t);
yt = @(t) exp(-t/ 10).*cos(5*t);
zt = @(t) t;
fplot3(xt, yt, zt, [-12 12], 'r-.')

三维曲面

一般步骤：

1. 平面网格数据的生成：一般使用meshgrid函数。
2. 选择合适的函数绘制三维曲面。

平面网格数据的生成

首先理解什么是网格数据？

下图，左下角为(2, 3)，右上角为(6, 8)的矩形区域，包含30个点，将这些点的x、y坐标都按照相对位置的关系分别赋值到两个矩阵X、Y中，可以得到$6\times 5$​的矩阵X，存储每个点的x坐标，和$6\times 5$的矩阵Y，存储每个点的y坐标。

得到平面网格数据就相当于得到了左下角为(2, 3)，右上角为(6, 8)的矩形区域内全部点的坐标了，对于每个点我们知道该点对应的z坐标，得到(x, y, z)三维坐标，就可以在坐标系中标注出来了，当知道坐标的点足够多时便可绘制出曲面。这就是绘制全面函数的原理。

对于上图而言，其X矩阵为：

X =2     3     4     5     62     3     4     5     62     3     4     5     62     3     4     5     62     3     4     5     62     3     4     5     6	

其Y矩阵为：

Y =3     3     3     3     34     4     4     4     45     5     5     5     56     6     6     6     67     7     7     7     78     8     8     8     8

手动生成

x= 2:6;
y = (3:8)';
X = ones(size(y))*x
Y = y*ones(size(x))

结果同上。

meshgrid函数

[X Y] = meshgrid(x, y)：x、y为向量，分别对应x坐标和y坐标，经测试行向量列向量均可。

[X Y] = meshgrid(x)：此时相当于x=y。

[X Y] = meshgrid(2:6, 3:8)

结果同上。

绘制三维曲面

mesh函数

mesh(x, y, z, c)：x、y为平面网格数据，即上面得到的X和Y，z为对应点的高度，也是上面提到的，x、y、z为同型矩阵，c用于指定在不同高度下曲面的颜色，一般省略，省略时c=z。

mesh(z, c)：当x和y省略时，z矩阵的第二维下标当作x轴坐标，z矩阵的第一维下标当作y轴坐标。

注意：与mesh用法类似的函数，如需要网格数据作为参数的函数，当网格数据对应的z坐标信息已经知道时，即题目已给出，则x、y参数可以为x坐标和y坐标的向量，无需使用meshgrid函数生成网格数据！之所以要生成网格数据，是因为大部分题目的xy对应的z坐标是未知的，因此要生成网格数据后代入满足的方程求解出对应的z坐标后才能进行绘制等操作。

t = 1:5;
z=[0.5*t; 2*t; 3*t];mesh(z);

surf函数

surf(x, y, z, c)：同上。

surf(z, c)：同上。

mesh函数与surf函数的区别

mesh函数用于绘制不是特别精细的三维曲面网格图，同一层面的线条用相同的颜色表示。

surf函数用于绘制比较光滑的三维曲面网格图，各线条之间的补面用颜色填充。

t = -2:0.2:2;
[X,Y] = meshgrid(t);
Z= X .* exp(-X.^2- Y.^2);subplot(131)
mesh(X,Y,Z);subplot(132)
surf(X,Y,Z);subplot(133)
plot3(X,Y,Z);grid on % 写在绘制图像下面才能生效

plot3函数此时的调用形式为三个参数为同型矩阵，则每一列表示一条曲线。

fsurf函数

fsurf(funx, funy, funz, uvlims)：funx、funy、funz代表定义曲面x、y、z坐标的函数，通常采用函数句柄的形式。uvlims为funx、funy和funz的自变量的取值范围,用4元向量[umin, umax, vmin, vmax]描述﹐默认为[-5,5,-5,5]。一般用于参数方程且参数方程中含两个参数。

fmesh函数

fmesh(funx, funy, funz, uvlims)：参数含义同上。一般用于参数方程且参数方程中含两个参数。

funx = @(u, v) u.*sin(v);
funy = @(u, v) -u.*cos(v);
funz = @(u, v) v;
fsurf(funx, funy, funz,[-5,5,-5,-2])
hold on
fmesh(funx, funy, funz,[-5,5,-2,2])
hold off

特殊的绘制三维曲面函数

meshc函数

带等高线的三维网格曲面函数。

用法同mesh。

meshz函数

带底座的三维网格曲面函数。

用法同mesh。

surfc函数

具有等高线的曲面函数。

用法同mesh。

surfl函数

具有光照效果的曲面函数。

用法同mesh。

[x,y]=meshgrid(0:0.1:2, 1:0.1:3);
z=(x-1).^2+(y-2).^2-1;
subplot(2,2,1);
meshc(x, y, z); title('meshc(x, y,z)')
subplot(2,2,2);
meshz(x, y, z) ; title('meshz(x, y,z)')
subplot(2,2,3);
surfc(x, y, z); title('surfc(x, y,z)')
subplot(2,2,4);
surfl(x, y,z); title('surfl(x, y,z)')

sphere函数

[x y z] = sphere(n)：绘制单位球，n为此球要通过多少个多边形平面围成，n越大越光滑，返回平面网格数据x和y，以及它们对应的高度，得到的x、y、z可以直接调用mesh类函数或surf类函数绘制球。

!!! 绘制任意球心，任意半径的球：

%% 绘制球：(x-10)²+(y-5)²+(z-3)²=10² 
a = 10; b = 5; c = 3; r = 10; % 用户定义或输入球心坐标和半径
[x y z] = sphere(30);
X = x*r + a;
Y = y*r + b;
Z = z*r + c;
surf(X, Y, Z)
title('(x-10)²+(y-5)²+(z-3)²=10² ')
grid on

cylinder函数

[x,y,z]=cylinder：函数返回一半径和高度都为1的圆柱体x，y，z轴的坐标值，圆柱体沿其周长有20个等距分布的点

[x,y,z]=cylinder®：函数一个半径为r、高度为1的圆柱体的x，y，z轴的坐标值，圆柱体沿其周长有20个等距分布的点

[x,y,z]=cylinder(r,n)：函数一个半径为r、高度为1的圆柱体的x，y，z轴的坐标值，圆柱体沿其周长有n个等距分布的点

此时生成的x、y、z是两行的矩阵。x的第一行与第二行相等，分别表示圆形上点的x坐标；y同理x；z的第一行是下底面的z坐标，z的第二行是上底面的z坐标，即0和1。

本质上，圆柱就是由两个圆形上的散点绘制而成。

!!! 绘制底面圆心任意，高度任意的圆柱：

a = -1; b = 2; up = 5; down = -2; % 底面圆心(a, b)，高度为[down, up]
[x y z] = cylinder(2, 30);
surf(x+a, y+b, repmat([-2;5], 1, length(x))) % 保证z与x同型，且每列都是-2 5
grid on

subplot(1,3,1);
[x y z]=cylinder; % 圆柱
surf(x, y, z);subplot(1,3,2);
t=linspace(0,2*pi,40);
[x y z]=cylinder(2+cos(t),30); % 花瓶
surf(x, y, z);subplot(1,3,3);
[x y z]=cylinder(0:0.2:2,30); % 圆锥
surf(x, y, z);

[x, y, z]= cylinder(1, 60);
z=[-1*z(2,:); z(2,:)]; % 高[-1, 1]
surf(x, y, z);
hold on
surf(y, z, x);
xlabel('x')
ylabel('y')
zlabel('z')
axis equal

图形修饰处理

视点处理

视点，即看物体的位置，看物体的位置不同，看到物体的样子也就不同；视点位置可由方位角和仰角表示。

方位角又称旋转角，视点与原点的连线在xoy面的投影与y轴负方向的夹角为方位角。正值表示逆时针，负值表示顺时针。

仰角又称视角，视点与原点的连线与xoy面的夹角。正值表示在xoy面上方，负值表示在xoy面下方。

view函数

view(az, el)：az为方位角，el为仰角，单位均为度；默认方位角为-37.5°，仰角为30°。

view(x, y, z)：在直角坐标系中直接设置视点位置为(x, y, z)

view(2)：观察物体的二维样式，即俯视图，等价于view(0, 90)

view(3)：观察物体的三维样式，即默认，等价于view(-37.5, 30)

[x, y]=meshgrid(0:0.1:2, 1:0.1:3);
z=(x- 1).^2+(y-2).^2-1;subplot(2,2,1); 
mesh(x, y, z) % 等价于view(3)
title('方位角=-37.5{\circ},仰角=30{\circ}')subplot(2,2,2); 
mesh(x, y,z)
view(0,90); % 等价于view(2)
title('方位角=0{\circ},仰角=90{\circ}')subplot(2,2,3); 
mesh(x, y, z)
view(90,0); 
title('方位角=90{circ},仰角=0{\circ}')subplot(2,2,4); 
mesh(x, y,z)
view(-45,-60); 
title('方位角=-45{\circ} ,仰角=-60{\circ}')

色彩处理

色图矩阵是若干行三列的矩阵，每个元素范围[0, 1]，0表示亮度为0，1表示亮度最大，三列分别表示RGB的颜色亮度，每行为颜色亮度的变化。

内建色图（自带色图）：

colormap函数

colormap cmapname：cmapname内建色图的名字，设置图像为此色图。

colormap(cmap)：cmap为色图矩阵，设置图像为此色图矩阵表示的色图。

surf(peaks)
colormap hot
% colormap(hot(64)) % 与上面等价，内建色图是64行的矩阵，hot(n)表示生成64行的热度色图矩阵，其他色图矩阵的生成方式一致。

自定义色图矩阵

c = 0:0.2:1;
cmap = [c' c' c'];
surf(peaks)
colormap(cmap) % 等价于colormap(gray(6))

%% 我比较喜欢的一个配色
mycolorpoint=[[0 0 16];[8 69 99];[57 174 156];[198 243 99];[222 251 123];[239 255 190]];
mycolorposition=[1 11 33 50 57 64];
mycolormap_r=interp1(mycolorposition,mycolorpoint(:,1),1:64,'linear','extrap');
mycolormap_g=interp1(mycolorposition,mycolorpoint(:,2),1:64,'linear','extrap');
mycolormap_b=interp1(mycolorposition,mycolorpoint(:,3),1:64,'linear','extrap');
mycolor=[mycolormap_r',mycolormap_g',mycolormap_b']/255;
mycolor=round(mycolor*10^4)/10^4;%保留4位小数peaks(20);
colormap(mycolor)

[配色来自](利用matlab构建自己的colormap（色彩搭配）_hyhhyh21的博客-CSDN博客_colormap hsv)

三维图形表面的着色

shading faceted：将每个网格片用其高度对应的颜色进行着色，网格线是黑色。
shading flat：将每个网格片用同一个颜色进行着色，且网格线也用相应的颜色。
shading interp：在网格片内采用颜色插值处理。

[x, y, z]= cylinder(pi:-pi/5:0, 10);
colormap(lines);subplot(1,3,1);
surf(x, y, z); 
shading flatsubplot(1,3,2);
surf(x, y, z); 
shading interpsubplot(1,3,3);
surf (x, y, z);
% 默认使用shading faceted

图形裁剪

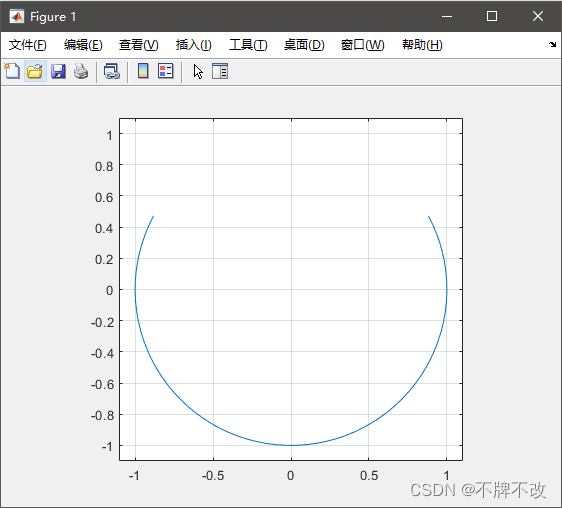
将图形中需要裁剪部分对应的函数值设置成NaN，这样在绘制图形时,函数值为NaN的部分将不显示出来，从而达到对图形进行裁剪的目的。

t = linspace(0,2*pi,100);
x= sin(t);
y = cos(t);
p = y > 0.5;
y(p)= NaN; % 将逻辑矩阵中为1的对应位置元素设置为NaN，即设置为不存在，但y的长度还是100plot(x, y)
axis([-1.1, 1.1, -1.1, 1.1])
axis square
grid on

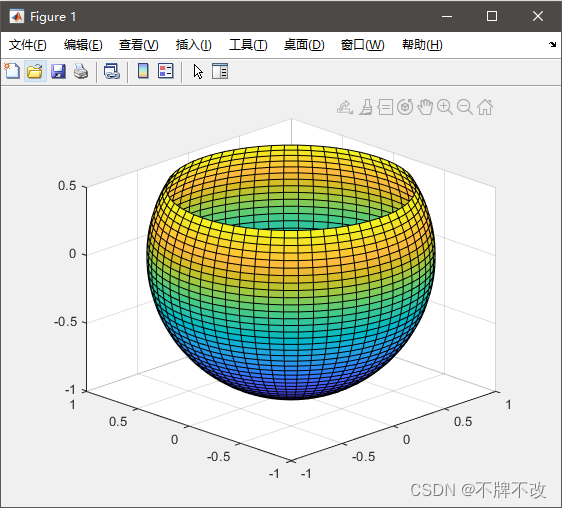
[X,Y,Z] = sphere(60);
p = Z>0.5;
Z(p)= NaN;
surf(X,Y,Z)
axis([-1,1,-1,1,-1,1])
axis equal
view(-45,20)

注意：A(B)：其中A为矩阵，B为逻辑矩阵，则相当于获取了B逻辑矩阵中为1的位置在A矩阵中对应位置的元素。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！