AVL树的实现

1.简述

AVL树本质是二叉查找树，与二叉查找树不同的是AVL树带有平衡条件
平衡条件： 每个节点的左子树和右子树的高度最多相差1，空树的高度为-1
插入分以下四种情况：

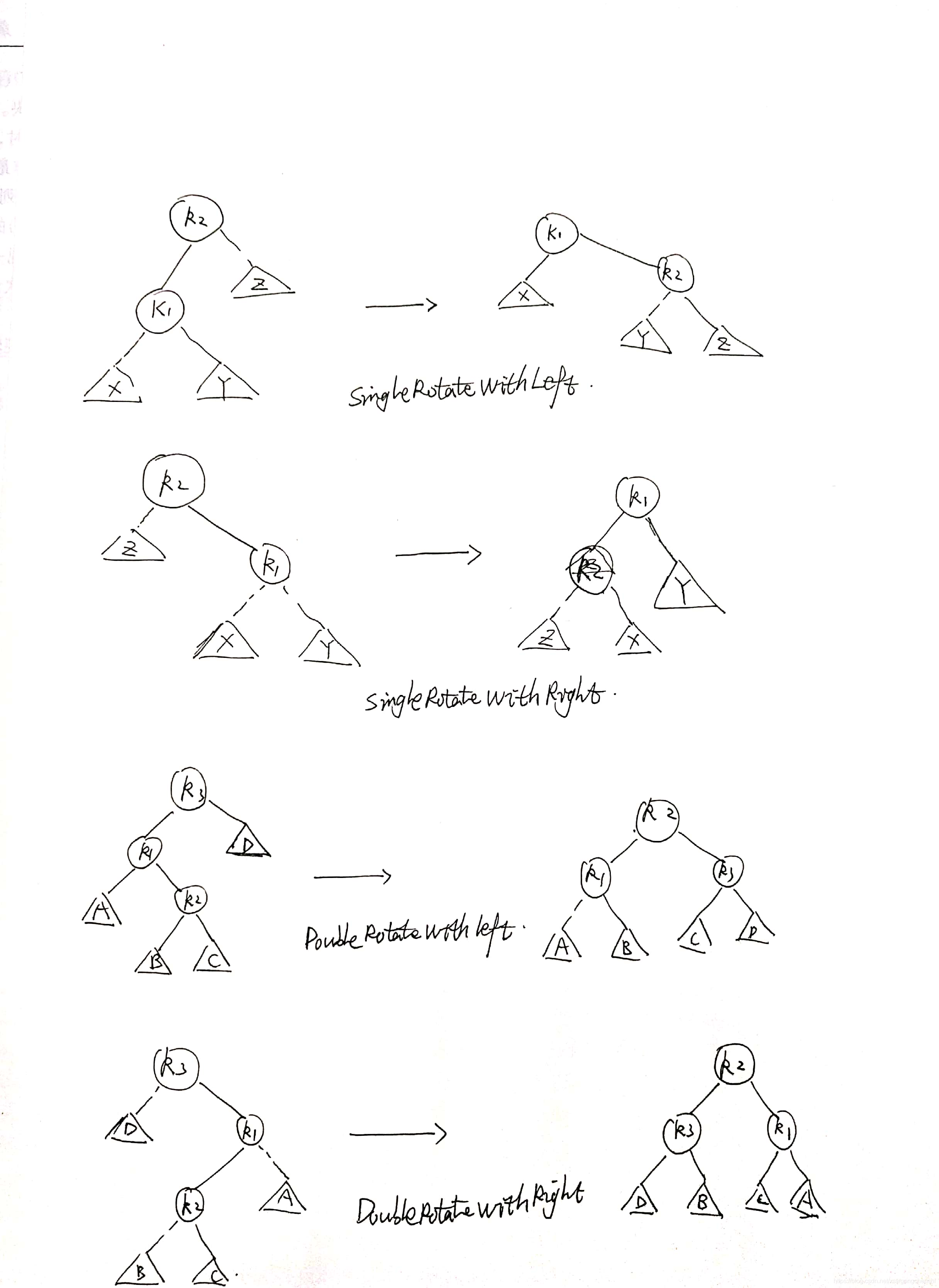
• 1 对a的左子树的左子树进行一次插入
• 2 对a的左子树的右子树进行一次插入
• 3 对a的右子树的左子树进行一次插入
• 4 对a的右子树的右子树进行一次插入
  （1/4情况为单旋；2/3情况为双旋转）
  

2.声明

#ifndef _AVL_H_
#define _AVL_H_class AvlNode;
typedef AvlNode* Position;
typedef AvlNode* AvlTree;class AvlNode {
public:int element;AvlTree left;AvlTree right;int height;		//记录树的高度
};int Height(Position p);
AvlTree MakeEmpty(AvlTree T);
Position FindMin(AvlTree T);
Position FindMax(AvlTree T);
Position Find(int element, AvlTree T);
AvlTree Insert(int element, AvlTree T);Position SingleRotateWithLeft(Position k2);
Position SingleRotateWithRight(Position k2);
Position DoubleRoateWithLeft(Position k3);
Position DoubleRoateWithRight(Position k3);
#endif // !_AVL_H_

3.实现

#include
#include"avl.h"
#include
using namespace std;int Height(Position p)
{if (p == NULL)return -1;elsereturn p->height;
}AvlTree MakeEmpty(AvlTree T)
{if (T != NULL){MakeEmpty(T->left);MakeEmpty(T->right);delete T;T = NULL;}return NULL;
}Position Find(int element, AvlTree T)
{if (T == NULL)return NULL;if (element<T->element)return Find(element, T->left);else{if (element>T->element)return Find(element, T->right);elsereturn T;}}//一直往左孩子走
Position FindMin(AvlTree T)
{if (T != NULL){while (T->left != NULL)T = T->left;}return T;
}Position FindMax(AvlTree T)
{if (T != NULL){while (T->right != NULL)T = T->right;}return T;
}/**
* 单旋
*/
Position SingleRotateWithLeft(Position k2)
{Position k1;k1 = k2->left;k2->left = k1->right;k1->right = k2;k2->height = max({ Height(k2->left),Height(k2->right)})+1;k1->height = max({Height(k1->left),k2->height})+1;return k1;
}Position SingleRotateWithRight(Position k2)
{Position k1;k1 = k2->right;k2->right = k1->left;k1->left = k2;k2->height = max({ Height(k2->left),Height(k2->right) }) + 1;k1->height = max({ Height(k1->right),k2->height }) + 1;return k1;
}/**
* 双旋
*//**
* 先进行一次单右旋，再进行一次单左旋
*/
Position DoubleRoateWithLeft(Position k3)
{k3->left = SingleRotateWithRight(k3->left);return SingleRotateWithLeft(k3);
}Position DoubleRoateWithRight(Position k3)
{k3->right = SingleRotateWithLeft(k3->right);return SingleRotateWithRight(k3);
}AvlTree Insert(int element, AvlTree T)
{if (T == NULL){T = new AvlNode();T->element = element;T->height = 0;T->right = T->left = NULL;}else{if (element < T->element){T->left = Insert(element, T->left);if (Height(T->left) - Height(T->right) == 2){if (element < T->left->element)SingleRotateWithLeft(T);elseDoubleRoateWithLeft(T);}}elseif (element>T->element){T->right = Insert(element, T->right);if (Height(T->right) - Height(T->left) == 2){if (element > T->right->element)T = SingleRotateWithRight(T);elseT = DoubleRoateWithRight(T);}}}//element 已经存在T->height = max({ Height(T->left),Height(T->right) }) + 1;return T;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！