读彬彬有礼压缩感知相关论文笔记4——凸优化问题
这篇文章看完,由于原博主写的很清楚明了,所以自己的理解并不多,这篇文章只能算是转载了~
原文地址:压缩感知中的数学知识:凸优化
1. n维空间两点间任意连线
对于任意两点x和y,来自n维空间的Rn(n维实欧氏空间),则对于0<=μ<=1,关系μx+(1-μ)y表示x和y连线之间的所有点。
这是不是一个大家都知道的结论啊,但为什么我就是想不明白呢?我来证明一下吧,简化到一维的情况,即x和y就是两个实数。
假设y>x(即y-x>0),在一维情况下,只要证明x<=μx+(1-μ)y<=y就可以了。
证明:
x-[μx+(1-μ)y]=(1-μ)x-(1-μ)y=(1-[μx+(1-μ)y]<=0(因为1-μ>=0,x-y<0)
所以x<=μx+(1-μ)y
y-[μx+(1-μ)y]=μ(y-x)>=0
所以μx+(1-μ)y<=y
得证!
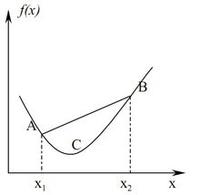
2. 凸函数
f[μx1+(1-μ)x2]<μf(x1)+(1-μ)f(x2) ,其中0<μ<1
其实,总结一下就是,函数中两点之间两线上的任一点的横坐标对应的函数值都要小于等于此横坐标对应的连线值。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!