分金子[2017年360春招笔试编程题]

如题 :

A、B两伙马贼意外地在一片沙漠中发现了一处金矿，双方都想独占金矿，但各自的实力都不足以吞下对方，经过谈判后，双方同意用一个公平的方式来处理这片金矿。处理的规则如下：他们把整个金矿分成n段，由A、B开始轮流从最左端或最右端占据一段，直到分完为止。 

马贼A想提前知道他们能分到多少金子，因此请你帮忙计算他们最后各自拥有多少金子?（两伙马贼均会采取对己方有利的策略）

解题思路 ：运用动态规划的算法思想求解最优解往往是有效的，动态规划与分治法的区别在于动态规划保存了先前的值，这里我们构建一个二维数组dp用来保存

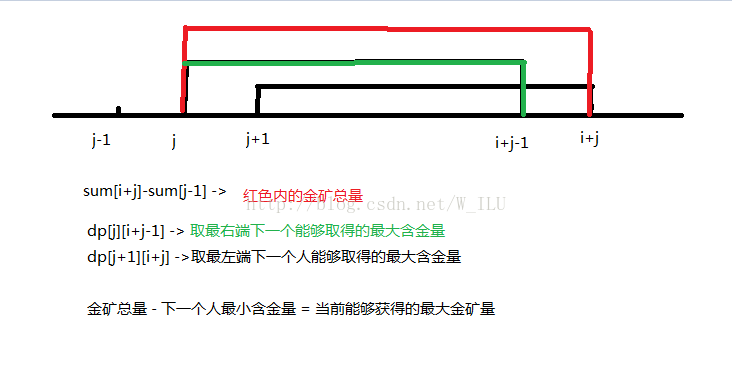
dp[x][y] -> 第x堆到第y堆的最优解，即含金量最高

min(dp[i+1][j],dp[i][j+1]) -> 下一个人拿到的最少的金矿

初始条件：dp[i][i]=a[i] //每一堆的金矿数

具体代码实现如下:public static void main(String[] args) {int t;//测试数据组数.Scanner in = new Scanner(System.in);t = in.nextInt();for (int k = 1; k <= t; k++) {int n;n = in.nextInt();int[][] dp = new int[n+1][n+1];//dp[x][y]保存第x堆到第y堆的最优解int[] a = new int[n+1];//每堆金矿含金量.int[] sum = new int[n+1];//n堆金矿总含金量.for (int j = 1; j <= n; j++) {a[j] = in.nextInt();sum[j] = sum[j-1] + a[j];dp[j][j] = a[j];}for (int i = 1; i < n; i++) {//外层循环控制for (int j = 1; j+i <= n; j++) {int t_sum = sum[i+j] - sum[j-1];//j1到j1+i1堆的总含金量int min_gold = Math.min(dp[j+1][i+j], dp[j][i+j-1]);//得到取最左端或者最右端的最小含金量dp[j][j+i] = t_sum-min_gold;//总含金量-最小含金量=最大剩余含金量}}System.out.println("Case #"+k+": "+dp[1][n]+" "+(sum[n]-dp[1][n]));}}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！