时间序列实战:指数平滑之能源需求预测
来源:TimeSeries
本文以Kaggle上一个能源需求预测的案例为基础,实战演示指数平滑(Holt-Winters)方法应用全流程。调用模型虽简单,但是入模前的数据分析、处理,模型参数的优化、效果的分析亦尤为重要,能够分析全面产出最优的方案又显得不那么简单。本文期望通过一个简单场景,回顾ML应用的基本流程。
Kaggle原文地址:https://www.kaggle.com/yashwanthmachiraju/forecasting-energy-demand/notebook
导入模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.holtwinters import ExponentialSmoothing读取数据
来自PJM超过10年的每小时能源消耗数据,单位:兆瓦。
df = pd.read_csv('data/PJME_hourly.csv')
df['Datetime'] = pd.to_datetime(df['Datetime'])
df.sort_values(by=['Datetime'], axis=0, ascending=True, inplace=True)
df.reset_index(inplace=True, drop=True)
print(df)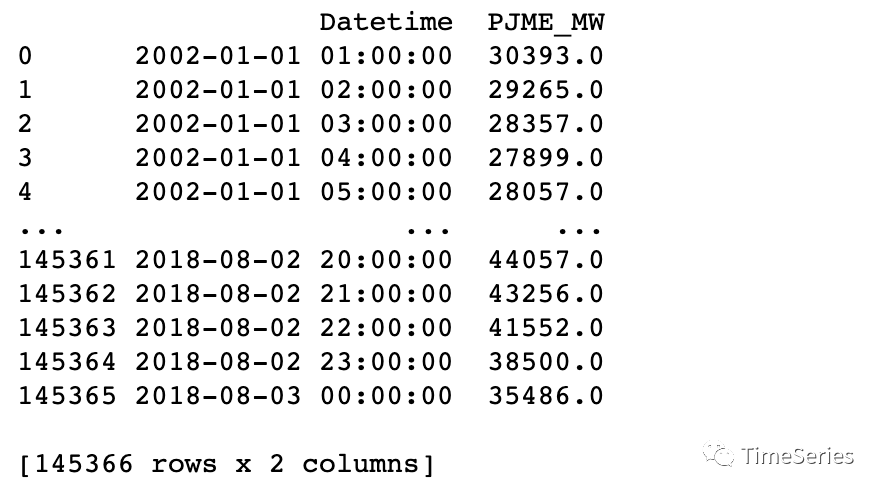
可视化
df.set_index('Datetime').plot(style='r', figsize=(20,4), legend=False)
plt.show()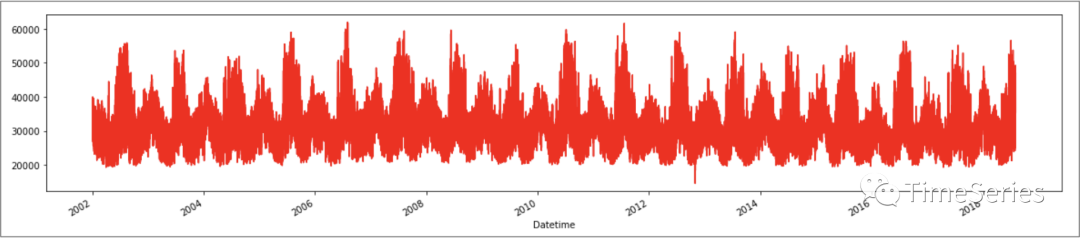
检查数据
从上图数据基本已经能看出数据时间范围、数据粒度、数据大体特征(周期型)、直观上是否有异常点(2012~2014貌似有一个)。
>> 那就先来看看数据是否有缺失值 -> 无。
print(df[pd.isnull(df['PJME_MW'])])>> 再来看看是否有异常值,结合数据可视化时的序列曲线图感觉2012~2014可能有异常值。进一步探索发现异常偏低数据集中在12年的10月30日当天。
print(df[df['PJME_MW'] <= 15000])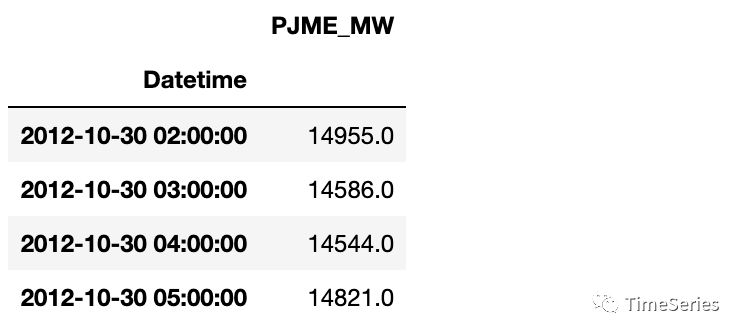
>> 但同往年趋势特征对比整体水平偏低但并无明显异常,所以决定对此不再做异常处理。
ts1 = df[(df['Datetime'] >= '2012-10-29 01:00:00') & (df['Datetime'] <= '2012-10-31 23:00:00')]['PJME_MW']
ts2 = df[(df['Datetime'] >= '2011-10-29 01:00:00') & (df['Datetime'] <= '2011-10-31 23:00:00')]['PJME_MW']plt.figure(figsize=(20,4))
ts1.reset_index(drop=True).plot(label='2012', legend=True)
ts2.reset_index(drop=True).plot(label='2011', legend=True)
plt.show()>> 下面接着再来看看时间粒度(读取数据时能看出来应该是小时级粒度)、是否等频(有无日期缺失、有无日期重复)。发现数据日期有重复且有日期缺失情况。(下图中黄色字体均值为1表明1小时1条)。
df['SPAN'] = df['Datetime'].diff().astype('timedelta64[h]').astype(float)
print(df.head())
print(df['SPAN'].median(), df['SPAN'].min(), df['SPAN'].max())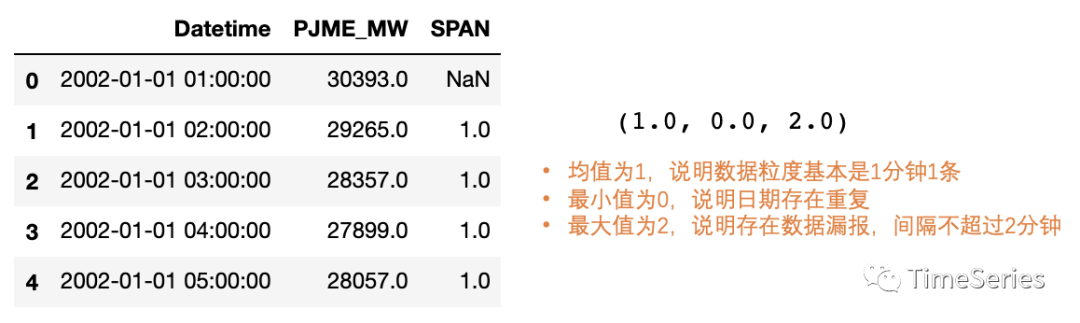
>> 既然数据日期有重复、有遗漏,不免好奇哪些重复、哪些遗漏,或者说重复&遗漏下数据的表现是怎样的。
# 日期重复数据
print(pd.merge(df, df[df['SPAN'] == 0]['Datetime'], on='Datetime'))# 漏报前后数据
index = df[df['SPAN'] == 2].index[0]
print(df.loc[index-3: index+3])# 漏报次数
print(df[df['SPAN'] == 2].shape[0]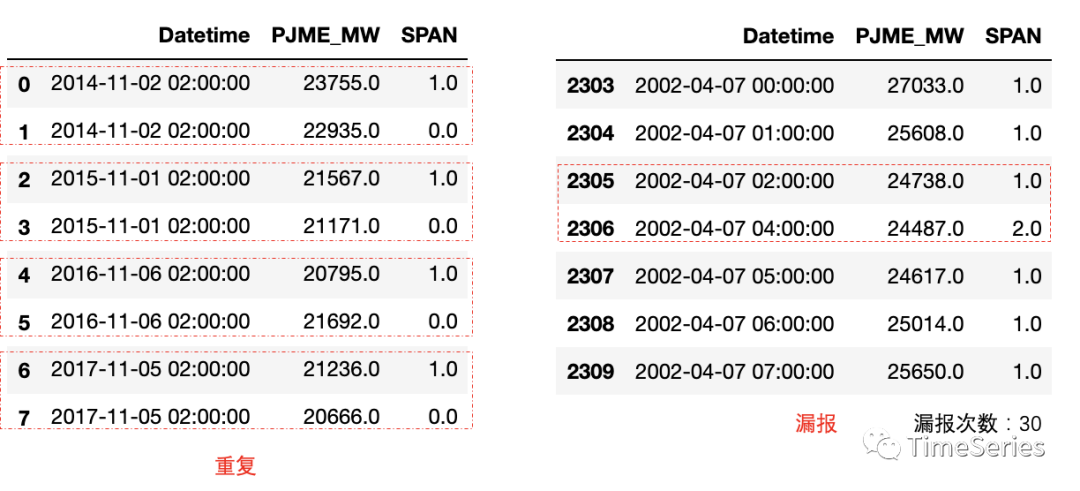
清洗数据
根据以上检查,发现数据相对还是比较干净的,但有2点问题:
1.日期有重复 -> 以上检查中可以看到数据并不是完全重复,猜测可能偶有一分钟内多次上传数据,此时为了数据粒度统一,舍弃较早的一条。
2.数据有漏报 -> 因传感器/网络等设施问题难免有数据漏报的情况,当前数据漏报间隔较短且漏报次数较少,可以使用插值的方法补充漏报数据。
# 去重
df.drop_duplicates(subset='Datetime', keep='last', inplace=True)# 插值
df.set_index('Datetime', inplace=True)
date_range = pd.date_range(start=df.index.min(), end=df.index.max(), freq='H')
df = df.reindex(date_range)
df['PJME_MW'].interpolate(method='linear', inplace=True)print(df)# 删除临时列
df.drop('SPAN', axis=1, inplace=True)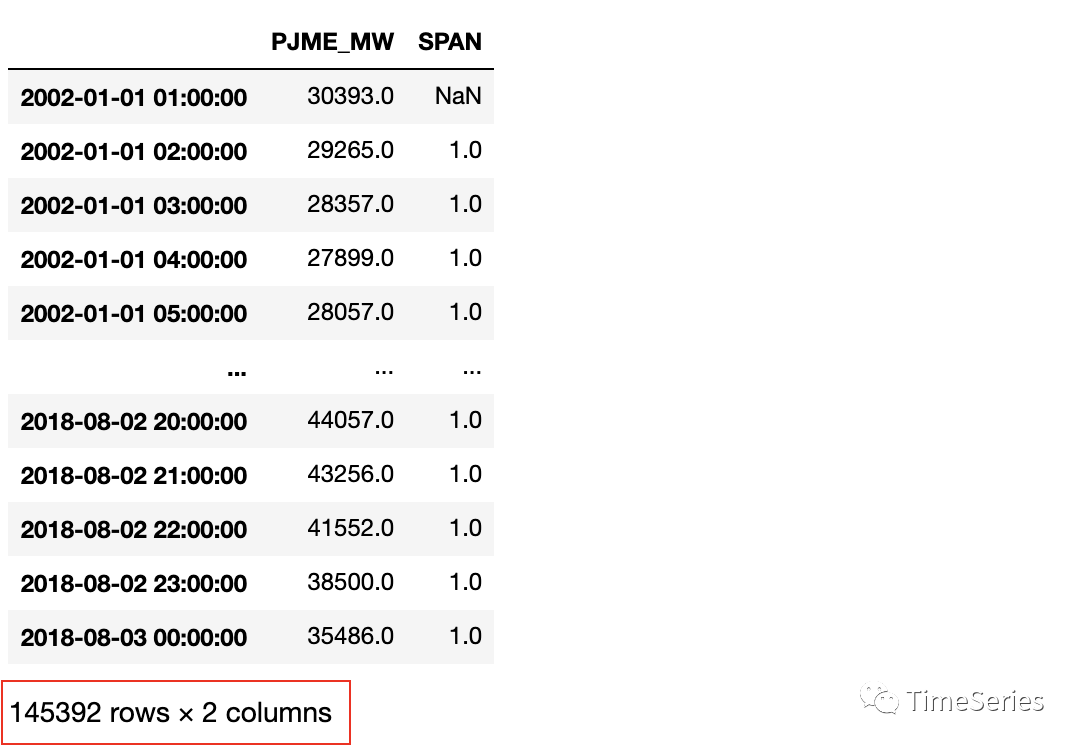
拆分训练集/验证集
需求为预测未来1年的数据,首先一个问题是不管用什么模型都至少要有一份数据能够验证模型效果。所以首先要拆分训练集和验证集,如果要更精确的验证模型效果还需拆分测试集。时间序列中一般根据时间拆分,较早的一段时间数据用于训练模型,最近的一段时间用于验证/测试模型效果。
比如我们要用过去5年的数据训练模型,可以留出最近1年的数据作为验证集,再往前推5年的数据做训练集。
train_years = 5
val_years = 1last_date = df.index[-1]
val_start_date = last_date - pd.DateOffset(years=val_years)
train_start_date = val_start_date - pd.DateOffset(months=train_years)print(train_start_date, val_start_date, last_date)
df_train = df.loc[(df.index >= train_start_date) & (df.index < val_start_date)]
df_val = df.loc[df.index >= val_start_date]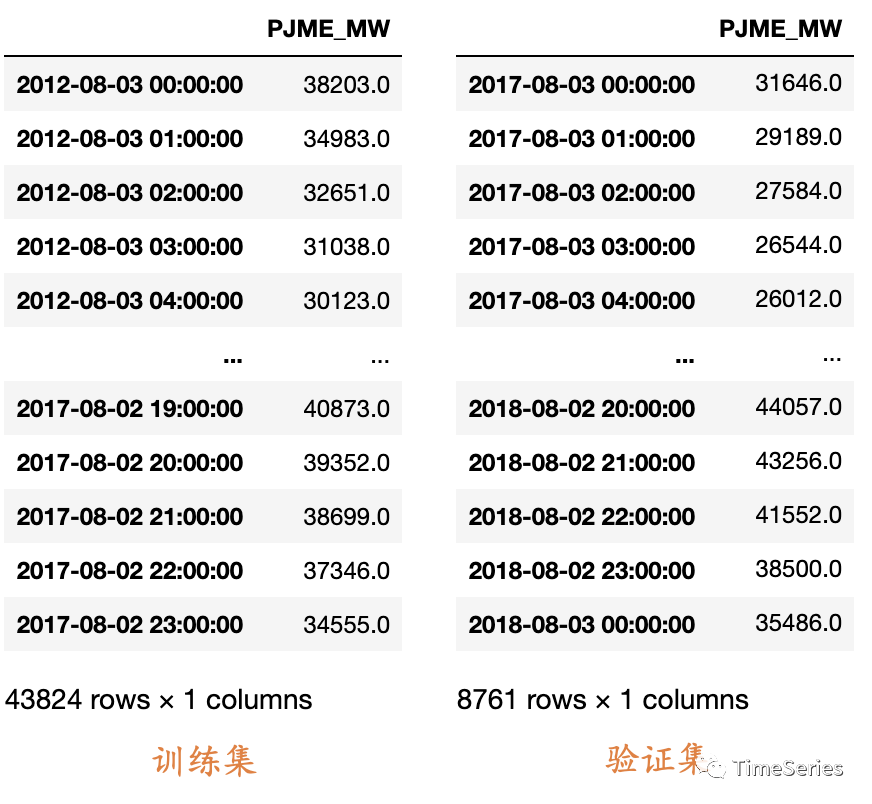
训练模型
模型选择
从数据的可视化图中能直观的看出来,当前数据为无趋势的周期型时间序列数据,周期大小为1年。本次限定使用指数平滑方法,有周期故使用三次指数平滑(Holt-Winters)方法,具体使用季节性加法模型还是乘法模型可进行实验根据评估指标选择。
模型训练
>> 评估指标:MAPE
def mape(y_true, y_pred):y_true, y_pred = np.array(y_true), np.array(y_pred)pe = (y_true - y_pred) / y_trueape = np.abs(pe)mape = np.mean(ape)return f'{mape*100:.2f}%'>> 训练模型
周期大小为24*365(一年,每天24个数据点),无趋势不指定trend,有季节性暂指定为加法模型。
模型训练时考虑数据量较大,设置模型参数初始值不进行暴力搜索,优化算法使用‘L-BFGS-B’,目的为提高计算速度,不然实在太慢。
periods = 24*365fit = ExponentialSmoothing(df_train['PJME_MW'],seasonal_periods=periods,seasonal='add').fit(method='L-BFGS-B', use_brute=False)
print(fit)
fcast = fit.forecast(len(df_val))mape_hw = mape(y_true=df_val['PJME_MW'], y_pred=fcast)
print(f'Our Holt-Winter model has a mean average percentage error of {mape_hw}')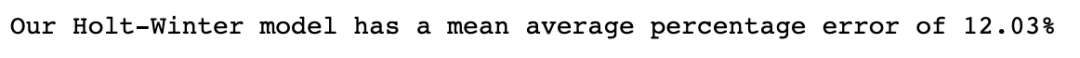
>> 参数调优
HW中的参数使用‘L-BFGS-B’优化算法自动优化,对比季节性加法模型,乘法模型效果较好MAPE为11.75%。
fit = ExponentialSmoothing(df_train['PJME_MW'],seasonal_periods=periods,seasonal='mul').fit(method='L-BFGS-B', use_brute=False)fcast = fit.forecast(len(df_val))mape_hw = mape(y_true=df_val['PJME_MW'], y_pred=fcast)print(f'Our Holt-Winter model has a mean average percentage error of {mape_hw1}')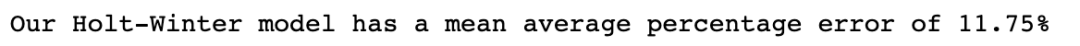
模型分析
通过进一步分析,认为使用7年数据训练模型效果较好,此时在近1年上的验证集上MAPE为9.7%。
分析内容有以下两点:
(1). 分析训练数据的大小对模型效果的影响
(2). 分析模型在不同年份上的表现看模型是否稳定
def test_train_size(df):val_years = 1periods = 24*365for train_years in range(1,10):# 拆分日期last_date = df.index[-1]val_start_date = last_date - pd.DateOffset(years=val_years)train_start_date = val_start_date - pd.DateOffset(years=train_years)# 训练集/验证集df_train = df.loc[(df.index >= train_start_date) & (df.index < val_start_date)]df_val = df.loc[df.index >= val_start_date]# 模型训练fit = ExponentialSmoothing(df_train['PJME_MW'],seasonal_periods=periods,seasonal='mul').fit(method='L-BFGS-B', use_brute=False)# 模型预测fcast = fit.forecast(len(df_val))# 模型评估mape_hw = mape(y_true=df_val['PJME_MW'], y_pred=fcast)# 打印结果if train_years == 1:val_date_desc = 'val_date_range : {}-{}'.format(val_start_date.strftime('%Y%m%d'), last_date.strftime('%Y%m%d'))print(val_date_desc)train_date_desc = 'train_date_range: {}-{}'.format(train_start_date.strftime('%Y%m%d'), val_start_date.strftime('%Y%m%d'))print(train_date_desc, 'train_years:', train_years, 'mape:', mape_hw)# 分析不同年数训练数据在18年(20170803-20180803)验证集上的表现
test_train_size(df)# 分析不同年数训练数据在17年(20160803-20170803)验证集上的表现
last_date = df.index[-1] - pd.DateOffset(years=1)
test_train_size(df.loc[df.index<=last_date])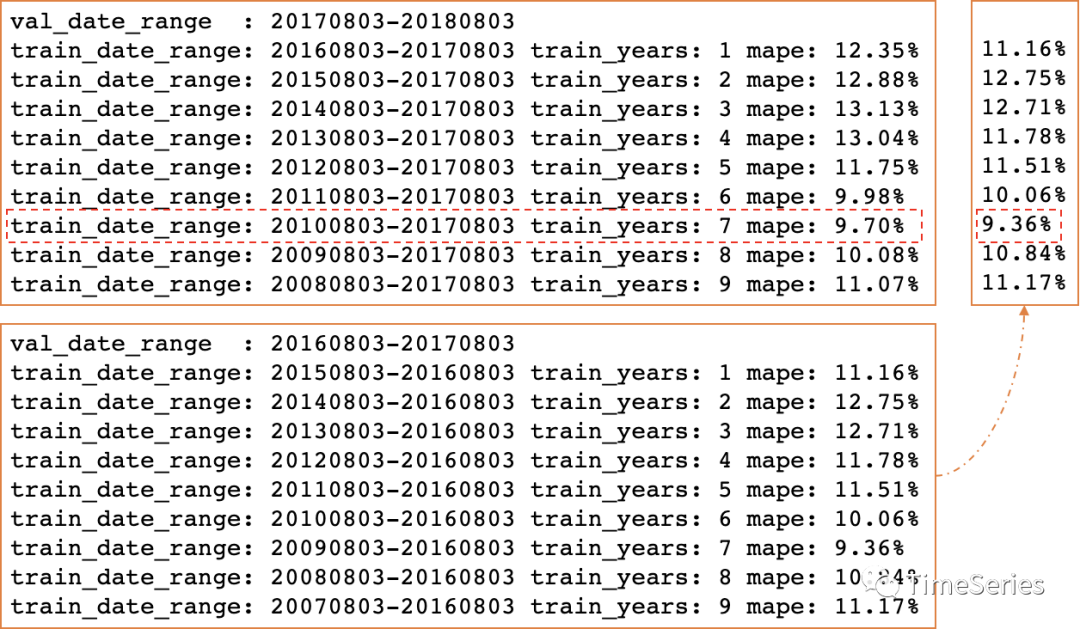
模型预测
确定训练数据时间跨度及模型各项参数后,使用最新数据重新训练模型,并预测未来一段时间的能源需求。
# 起始日期
last_date = df.index[-1]
train_start_date = last_date - pd.DateOffset(years=7)# 训练集
df_train = df.loc[df.index >= train_start_date]# 模型训练
fit = ExponentialSmoothing(df_train['PJME_MW'],seasonal_periods=periods,seasonal='mul').fit(method='L-BFGS-B', use_brute=False)# 模型预测
fcast = fit.forecast(24*365)
date_range = pd.date_range(start=df_train.index.min(), end=fcast.index.max(), freq='H')
df_train = df_train.reindex(date_range)
df_train['predict'] = fcastprint(fcast.index.min(), fcast.index.max())# 可视化
plt.figure(figsize=(20,4))
df_train['PJME_MW'].plot()
df_train['predict'].plot()
plt.xlabel('Date & Time')
plt.ylabel('Energy Demand [MW]')
plt.title('Holt-Winter Forecast of Hourly Energy Demand')
plt.show()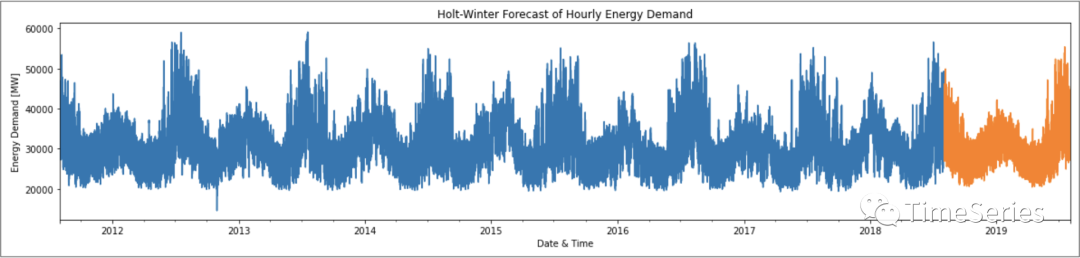
-------- End --------

精选资料
回复关键词,获取对应的资料:
| 关键词 | 资料名称 |
|---|---|
| 600 | 《Python知识手册》 |
| md | 《Markdown速查表》 |
| time | 《Python时间使用指南》 |
| str | 《Python字符串速查表》 |
| pip | 《Python:Pip速查表》 |
| style | 《Pandas表格样式配置指南》 |
| mat | 《Matplotlib入门100个案例》 |
| px | 《Plotly Express可视化指南》 |
精选视频
可视化: Plotly Express
财经: Plotly在投资领域的应用 | 绘制K线图表
排序算法: 汇总 | 冒泡排序 | 选择排序 | 快速排序 | 归并排序 | 堆排序 | 插入排序 | 希尔排序 | 计数排序 | 桶排序 | 基数排序

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!