概率论的学习整理--番外2：和二项式，组合相关的杨辉三角

1 杨辉三角

下面2个图，来自于百度百科，内容我整理了一些，确实是很有意思的

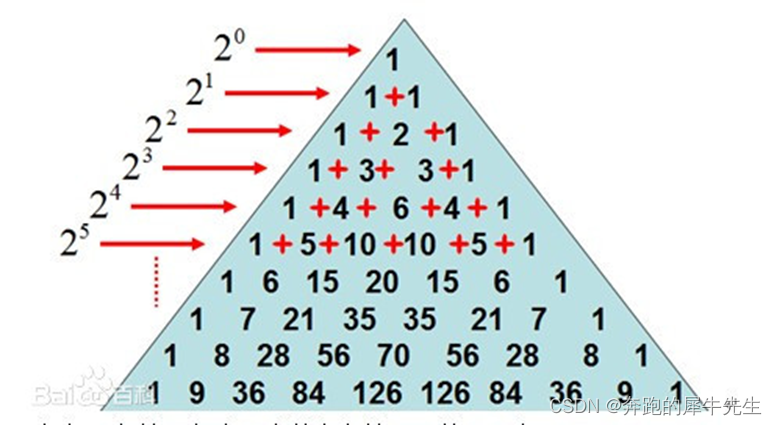
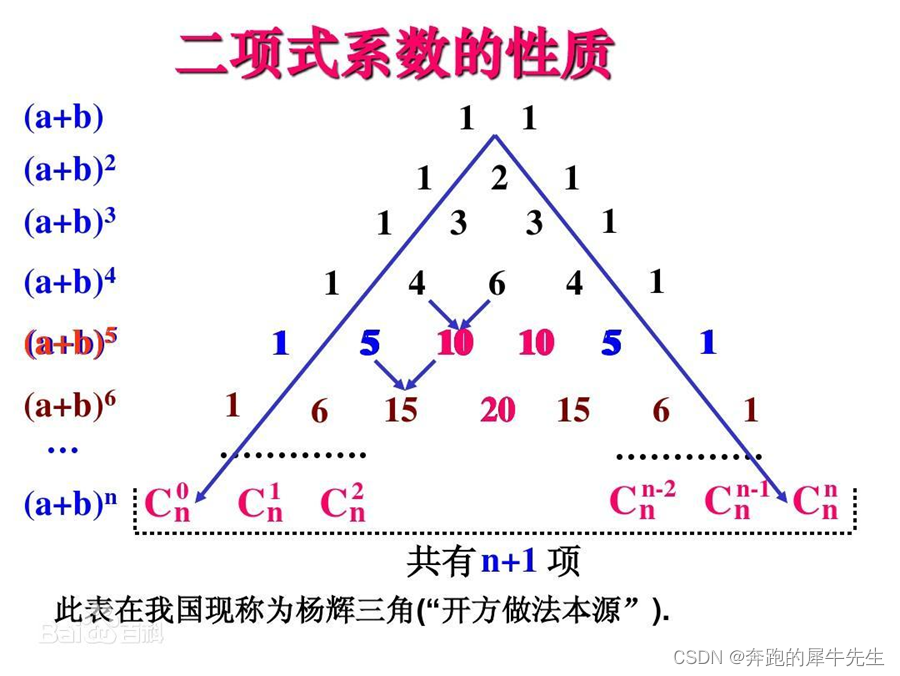
2 杨辉三角的一些神奇规律总结

2.1 直观看可以总结的规律

• 每个下层的数，都是上层相邻的两个数之和

2.2 和二项式对应的规律

• 每层的数，列举出来，刚好就是 (a+b)^n 的展开的所有系数 ，其中n=层数     
• 展开式，合并同类项之前，刚好是2^n个项数                
• 合并同类项后，项数（系数）数量  刚好也是 n+1个                

二项式相关

• (a+b)^n                
• =(a+b)*(a+b)^n-1                
• (a+b)必然是2项，乘(a+b)^n-1，就是2^n个展开项，但是可以合并为n+1项                

二项式定理

• (a+b)^n=C(n,0)*a^n*b^0+C(n,1)*a^n-1*b^1+…+C(n,n)*a^0*b^n

二项式系数之和

• 当a=1,b=1时
• (a+b)^n=2^n= C(n,0)+C(n,1)+…+C(n,n)

2.3  二进制的枚举      

• 二项式的展开是杨辉三角
• 同时2项式 = 2^n
• 这样，2^n 展开的这一系列 2^0，2^1，2^2....... 这不就是二进制吗？      

         
2.4  印度数学的视角              

• 如果把杨辉三角的多个数连起来，看成1个数字，比如第1层看成11，第2层看成121
• 每层之间，数值之间可以乘11                
• 那么每层都是11的指数函数，11^0，11^1，11^2  ... ...              
• 这个是从小孩的一本印度数学书上看来的，虽然初看起来花里胡哨，但是这个杨辉三角的解释还是很有道理的。。。。所以印度那边教数学，用*11乘，搞了一个速算方法

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！