“符号三角” 问题的回溯法求解方法

“符号三角” 问题的回溯法求解方法

符号三角问题：下面都是“-”。 下图是由14个“+”和14个“-”组成的符号三角形。2个同号下面都是“+”，2个异号下面都是“-”。

在一般情况下，符号三角形的第一行有n个符号。符号三角形问题要求对于给定的n，计算有多少个不同的符号三角形，使其所含的“+”和“-”的个数相同。
实现如下功能：
1.分别输出n的值为1----20时，对应的符号三角形个数，如没有满足条件的符号三角形，则输出0
代码：
public class TRAN {
static int n;//第一行的符号个数
static int half;//n*(n+1)/4
static int count;//当前“+”或者“-”的个数
static int[][] p;//符号三角形矩阵
static long sum;//已找到的符号三角形的个数
public static float Compute(int nn) {

	n = nn;count = 0;sum = 0;half = (n*(n+1))>>1;if((half>>1)<<1 != half) {return 0;}half = half>>1;p = new int[n+1][n+1];backtrack01(1);return sum;
}
public static void backtrack01(int t) {if(count>half || (t*(t-1)/2-count > half)) {//对题解树的剪枝return;}if(t>n) {sum++;//符号三角形的总数目+1}else {//每个位置都有两种情况0,1for(int i = 0;i<2;i++) {p[1][t] = i;count += i;//对"-"个数进行技术，为了进行剪枝操作//接下来绘制其余的n-1行for(int j = 2;j<=t;j++) {//通过异或的方式求其余行数的放置方式p[j][t-j+1] = p[j-1][t-j+1]^p[j-1][t-j+2];count += p[j][t-j+1];	}backtrack01(t+1);//恢复现场for(int j = 2;j<=t;j++) {count -= p[j][t-j+1];}count -= i;}}
}
public static void main(String[] args) {// TODO Auto-generated method stubint n;for(n=1;n<=20;n++) {float SUM = Compute(n);	System.out.println("n的值为"+n+"时对应的符号三角形总数： " + SUM);}
}

}

运行截图：

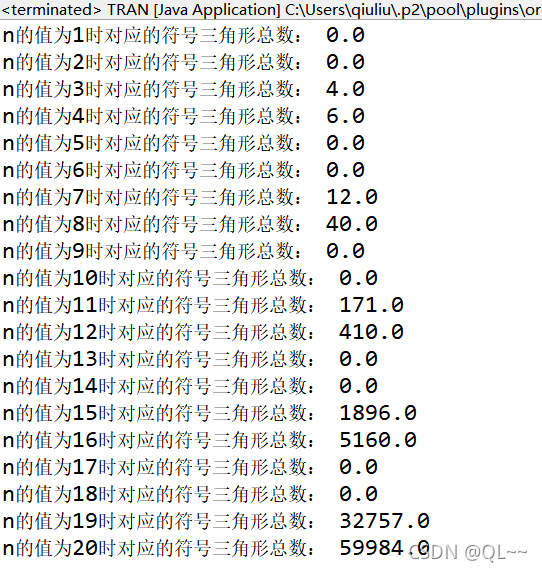
2.输入一个整数n，输出对应的符号三角形的个数，并依次显示出所有的符号三角形。
代码：

public class TRAN {static int n;//第一行的符号个数static int half;//n*(n+1)/4static int count;//当前“+”或者“-”的个数static int[][] p;//符号三角形矩阵static long sum;//已找到的符号三角形的个数public static float Compute(int nn) {n = nn;count = 0;sum = 0;half = (n*(n+1))>>1;if((half>>1)<<1 != half) {return 0;}half = half>>1;p = new int[n+1][n+1];backtrack(1);return sum;}public static void backtrack(int t) {if((count>half)||((t*(t-1)/2-count > half))) //对题解树的剪枝return;if(t>n) {sum++;//打印符号三角形for(int i =1;i<=n;i++) {for(int k = 1;k

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！