【论文精度】PARR

《Semantic Communications with Discrete-time Analog Transmission A PAPR Perspective》

原文链接

对时间离散幅度连续的信号（DTAT）进行JSCC传输（DTAT对性能提升有帮助，故研究之），会有产生PAPR过高的问题，采取OFDM调制后，PAPR过高的问题会加剧。所以提出问题：DeepJSCC的reconstruction performance是否以牺牲PAPR换取？作者从三个角度减少PAPR，分别是：线性预编码OFDMA、clipping、整合PAPR loss。
实验结果证明：
clipping操作（整合到训练过程）在PSNR下降不多的情况下，Γ−3大幅下降，较好地实现reconstruction performance与PAPR间的trade-off

1.基础知识

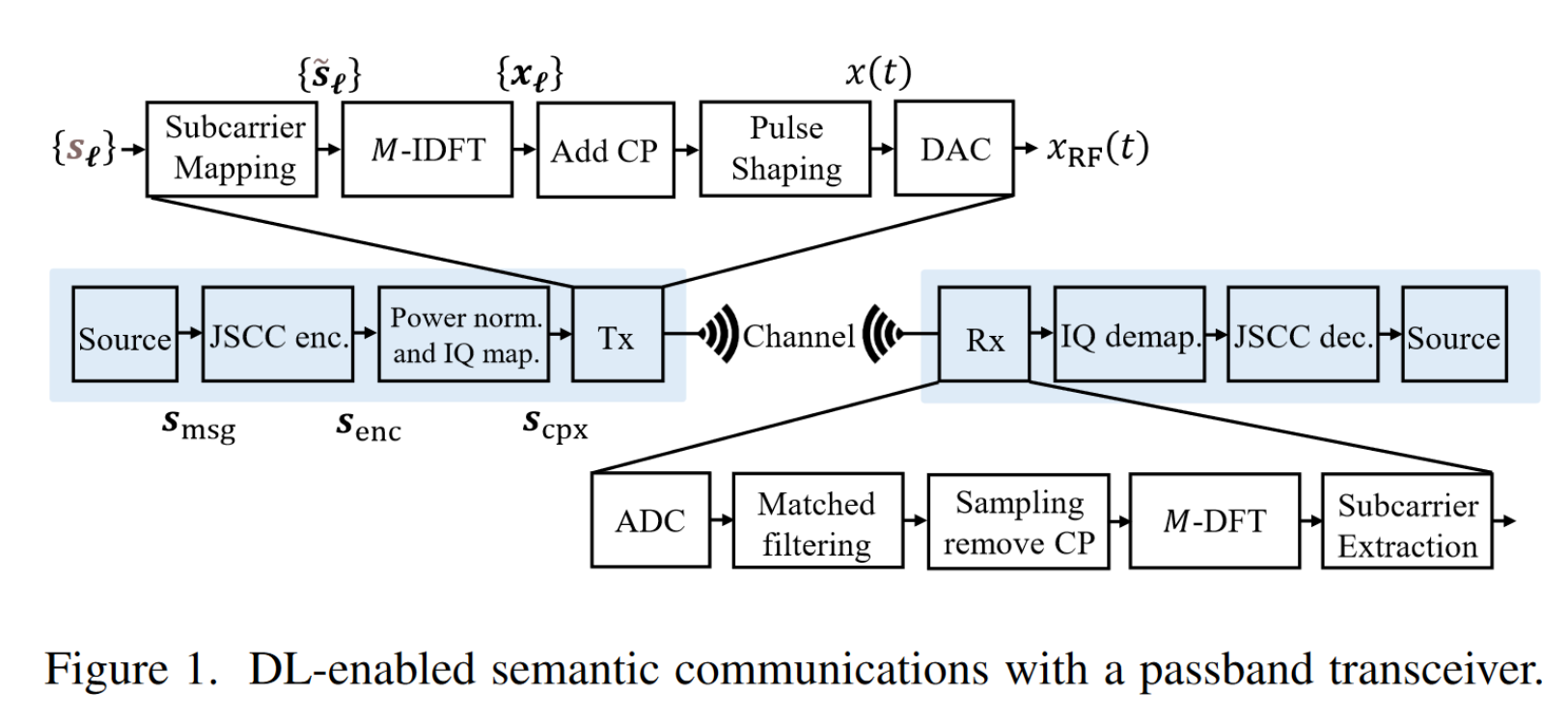
1.1.有必要深入理解OFDM

知乎这篇回答[1]，作者讲的很好。

1.1.1.基本介绍

OFDM是一种特殊的多载波传输方案，它可以被看作是一种调制技术，也可以被当作一种复用技术。

简单来说：OFDM是一种多载波的传输方法，它将频带划分为多个子信道并行传输数据，将高速数据流分成多个并行的低速数据流，然后调制到每个信道的子载波上进行传输。由于它将非平坦衰落无线信道转化成多个正交平坦衰落的子信道，从而可消除信道波形间的干扰，达到对抗多径衰落的目的。

正交频分复用（OFDM）是对多载波调制（MCM）的一种改进，在。它的特点是：各子载波相互正交，所以扩频调制后的频谱可以相互重叠，不但减少了子载波间的相互干扰，还大大提高了频谱利用率。

选择OFDM的一个很大的原因是该系统能够很好的对抗频率选择性衰落和窄带干扰。在单载波系统中，一次衰落或者干扰会导致整个链路失效，但是在多载波系统中，某一时刻只会有少部分的子信道受到深衰落的影响。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-euACzeue-1680007322623)(null)]

实际上这里IFFT充当的是一个实现子载波正交的作用，具体可以推导其DFT公式。

​ X ( k ) = ∑ n = 0 N − 1 x ( n ) e − j 2 π n k N X(k)=\sum_{n=0}^{N-1} x(n) e^{-j \frac{2 \pi n k}{N}} X(k)=n=0∑N−1​x(n)e−jN2πnk​

1.1.2.保护间隔

多径信道会对OFDM符号造成符号间干扰（Inter Symbol Interference，ISI）影响，加入循环前缀（cp）解决之。OFDM中由于子载波间正交，因此不会产生载波间干扰（Inter Carrier Interference，ICI）

OFDM将高速串行信号变成低速的并行信号，码元速率降低（码元周期变长，只要大于最大时延扩展，就可以避免ISI），实现带宽小于相干带宽[2]。

1.1.3.PARR

参考[3]

通带信号PARR的定义
ρ = max ⁡ ∣ x R F ( t ) ∣ 2 E [ ∣ x R F ( t ) ∣ 2 ] \rho=\frac{\max \left|x_{\mathrm{RF}}(t)\right|^2}{\mathbb{E}\left[\left|x_{\mathrm{RF}}(t)\right|^2\right]} ρ=E[∣xRF​(t)∣2]max∣xRF​(t)∣2​
累积分布函数(Cumulative Distribution Function，CDF)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。一般以大写CDF标记,，与概率密度函数probability density function（小写pdf）相对。
对于所有实数 ，累积分布函数定义如下：
F X ( x ) = P ( X ≤ x ) F_X(x)=\mathrm{P}(X \leq x) FX​(x)=P(X≤x)
即累积分布函数表示：对离散变量而言，所有小于等于a的值出现概率的和。

互补累计分布函数（Complementary Cumulative Distribution Function，CCDF） 为了表示OFDM系统中的峰均值PAPR的统计特性所引入的的概念，它定义为多载波传输系统中峰均值超过某一门限值z的概率。互补累积分布函数是对连续函数，所有大于a的值，其出现概率的和。
$F(a)=P(x>a)$

Epoch: 99
[========================>] Step: 196/196
test_PSNR, = meanPAPR (27.8304, array(12.127043, dtype=float32))
Saving…

和单载波系统相比，多载波系统有很高的峰值-平均功率比（Peak to Average Power Ratio，PAPR）

举个数值例子，假设N=12，M=4。OFDMA系统有12个子载波，给甲乙丙3个用户用，则每个用户可以分配到4个子载波呢。那甲乙丙三个用户，占据的是这12个子载波中的哪几个呢？这便是系统如何给用户分配子载波的方式。

DFDMA在整个频带(共有N个子载波)分配M点DFT 的输出同时对没有使用的N-M个子载波全部填充零。

LFDMA将DFT 的输出分配给(在N个子波中)M个连续的子载波。

当以N/M=S的距离等间隔分配 DFT 的输出时，DFDMA 被称为交织IFDMA，其中S称为带宽扩频因子。

2.实验

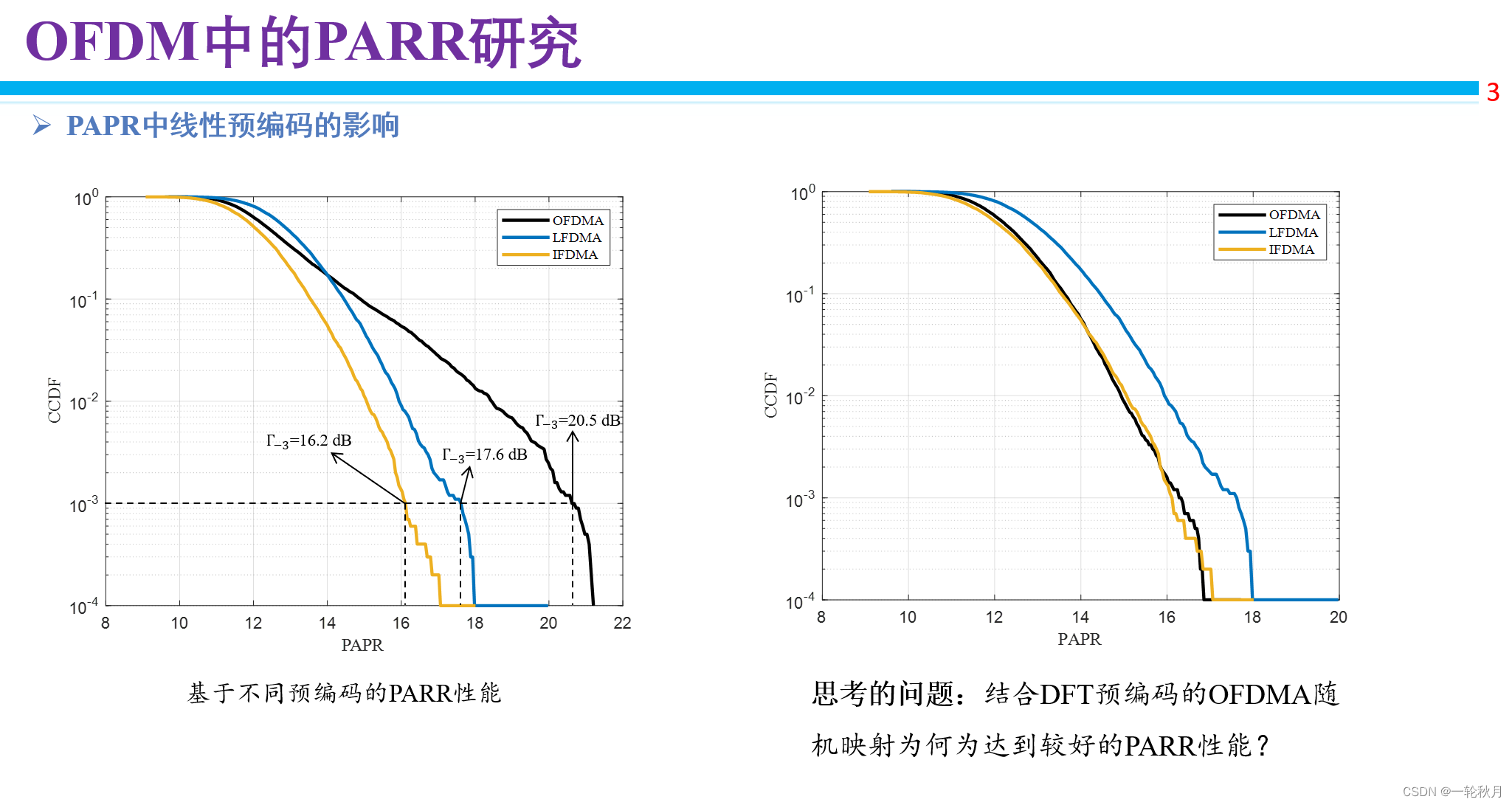
PAPR中线性预编码的影响

OFDMA

bestPSNR: 27.82, MSE: 0.0017, PAPRdB: 12.9373
test_PSNR, = meanPAPR (27.88753, array(12.828785, dtype=float32))

LFDMA：随机选一段N个用户

bestPSNR: 27.79, MSE: 0.0020, PAPRdB: 13.6895
test_PSNR, = meanPAPR (27.8111, array(13.02143, dtype=float32))

IFDMA：以扩频因子为步频选取一段

bestPSNR: 27.87, MSE: 0.0019, PAPRdB: 12.3999
test_PSNR, = meanPAPR (27.87126, array(12.176988, dtype=float32))

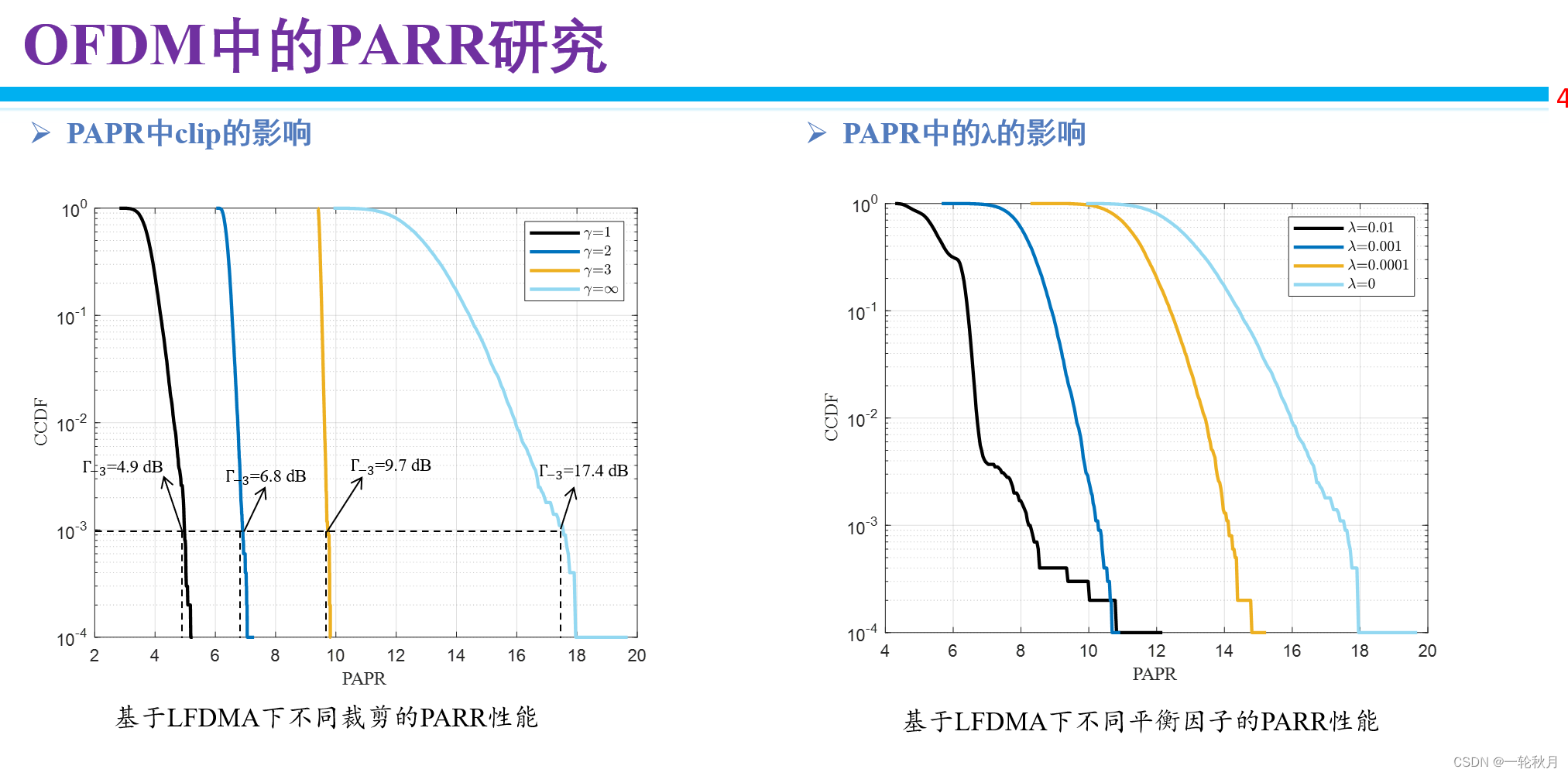
PAPR中clipping的影响

clipping = 1

test_PSNR, = meanPAPR (25.49916, array(3.8139226, dtype=float32))

clipping = 2

test_PSNR, = meanPAPR (27.31314, array(6.4135785, dtype=float32))

clipping = 3

test_PSNR, = meanPAPR (27.76343, array(9.475132, dtype=float32))

clipping = $\infty$
test_PSNR, = meanPAPR (27.8111, array(13.02143, dtype=float32))

PAPR中$\lambda$的影响

$\lambda$ = 0.01

test_PSNR, = meanPAPR (20.08668, array(5.6028976, dtype=float32))

$\lambda$ = 0.001

test_PSNR, = meanPAPR (24.97748, array(7.9412856, dtype=float32))

$\lambda$ = 0.0001

test_PSNR, = meanPAPR (27.62848, array(11.429363, dtype=float32))

$\lambda$ = 0

test_PSNR, = meanPAPR (27.8111, array(13.02143, dtype=float32))

2.1.为何三种线性预编码的结果与预期不符？

因为OFDMA无需预编码，搞清楚预编码和映射是两个概念

参考：

[1].OFDM完整仿真过程及解释（MATLAB）

[2].再谈符号间干扰（一）

[3].第9章：OFDM减小PAPR（1）——DFT扩频

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！