标量，矢量（向量），张量，空间，维度，矩阵，几何

概念

标量：0阶的张量（1维的空间？），一个具体的数值

向量（矢量）：1阶的张量（1*n）（n 维的空间？n 是2，则是2维空间，n是3,则是3维空间），eg：{（x,y）}是平面坐标点的1个1阶张量，有两个基量，{（x,y,z）}是空间坐标内的1阶张量，有三个基量，（一个有属性的数值？？？）

张量：2阶的张量（n*n），eg{(x1,y1),(x2,y2)}是平面坐标点的1个2阶张量，有4个基量，{（x1,y1,z1）(x2,y2,z2)}是空间坐标点的2阶张量，有9个基量，（常用来表示一个集合？？？一个有属性数值的集合？？）

3阶张量

张量百科：What's a Tensor_趣味科普人文_科技_bilibili_哔哩哔哩

张量满足与坐标系的选择无关的特性，是矢量概念的推广，矢量是一阶张量。张量是一个定义在一些向量空间和一些对偶空间的笛卡尔积上的多重线性映射，其坐标是|n|维空间内，有|n|个分量的一种量，其中每个分量都是坐标的函数，而在坐标变换时，这些分量也依照某些规则做线性变量，r称为该张量的秩或阶（与矩阵的秩和阶没有关系），

对于3维空间，r=1时的张量为向量，（x,y,z）,张量分成协变张量（指标在下），逆变张量（指标在上）混合张量（指标在上和指标在下）

向量计算

（觉得这是在笛卡尔坐标系下的成立的）

向量的内积（又名：点乘，点积,向量的积）

点乘，可以看作一个向量在另一个向量上投影后的大小，没有方向信息（可以理解为降维？？），结果是一个标量（如果是3维向量，点乘的结果是不是应该还是一个向量？？）。

公式：a . b =|a|*|b| * cosθ

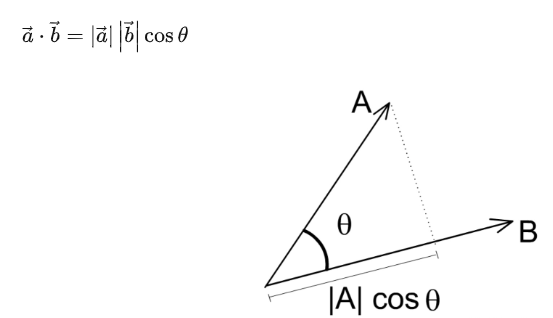
 方向关系：

 a·b>0    方向基本相同，夹角在0°到90°之间

 a·b=0    正交，相互垂直  

 a·b<0    方向基本相反，夹角在90°到180°之间 

推导：

向量的外积（又名：叉乘，叉积，矢积，向量积）

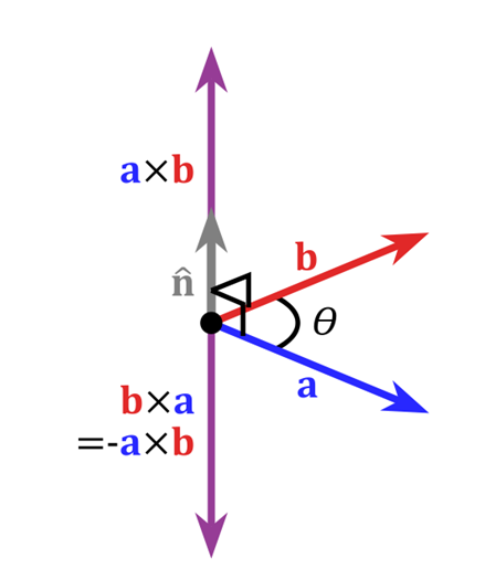
叉乘，可以看作一个向量和另一个向量共面后（两点共线，三点共面，向量有个相同的初始点，所以两个不平行的向量可以确定一个平面），在面的法向量上的大小，结果是一个向量（升维？？），方向是法向量的方向（右手定则），与原始两个向量垂直

公式：a x b=|a||b|sinθ  

 a x b 或者写作a ^ b (防止叉乘符号与字母X 混淆)；

坐标运算：

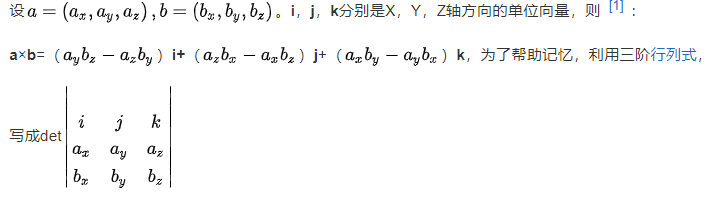
注：

行列式运算：

r：row 行;c:colum 列

i =(-1)^(1(r)+1(c)）*(AyBz-ByAz)=-1^2 *(AyBz-ByAz)=AyBz-ByAz=AyBz-AzBy

j=(-1)^(1(r)+2(c)）*(AxBz-BxAz)=-1^3 *(AxBz-BxAz)=BxAz-AxBz=AzBx-AxBz

k=(-1)^(1(r)+3(c)）*(AxBy-BxAy)=-1^4 *(AxBy-BxAy)=AxBy-BxAy=AxBy-AyBx

代数规则：

 混合积[abc]=（a×b）·c可以得到以a，b，c为棱的平行六面体的体积

1、反交换律：a×b=(-)b×a

2、加法的分配律：a×（b+c）=a×b+a×c。

3、与标量乘法兼容：（ra）×b=a×（rb）=r（a×b）。

4、不满足结合律，但满足雅可比恒等式：a×（b×c）+b×（c×a）+c×（a×b）=0。

5、分配律，线性性和雅可比恒等式别表明：具有向量加法和叉积的R3构成了一个李代数。

6、两个非零向量a和b平行，当且仅当a×b=0

注：

三维向量叉乘可以得到四元数，七维向量叉乘可以得到八元数

点乘和叉乘区别：

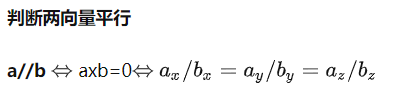
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！