《数据结构》自学考试 课程代码02331 2012版 第05章 树和二叉树 例题集和编程练习

- OS: Mac Catalina 10.15.4
- Hardware: Intel Core i9/16G 2667MHz DDR4
- 编译器版本:Mac Xcode 11.6
第05章 树和二叉树
目录
5.1 二叉树
5.1.1 二叉树的链式存储结构
5.2 二叉树运算
5.2.1 按广义表表示二叉树结构生成二叉链表的算法
5.2.2 按完全二叉树的层次顺序依次输入结点信息建立二叉链表的算法
5.2.3 二叉树的递归遍历算法
5.2.3.1 前序遍历二叉树算法
5.2.3.2 中序遍历二叉树算法
5.2.3.3 后序遍历二叉树算法
5.2.3.4 二叉树递归便利示例
5.2.4 二叉树的非递归遍历算法
5.2.4.1 利用栈的非递归中序遍历算法
5.2.4.2 利用栈的非递归中序遍历算法(指针数组版)
5.2.4.3 利用栈的非递归前序遍历算法
5.2.4.4 非递归的按层遍历二叉链表树
5.2.5 综合例题
5.2.5.1 例题1 前序、中序、后续输出二叉树
5.2.5.2 例题2 求二叉树深度
5.2.5.3 例题3 在二叉树中查询结点并计算二叉结点的层次
5.3 线索二叉树
5.3.1 二叉树的线索化
5.3.1.1 二叉链表加中序线索
5.3.2 二叉线索链表上的运算
5.3.2.1 查找某结点*p的后继结点
5.3.2.2 线索二叉树的遍历
5.4 数和森林
5.4.1 数的存储结构
5.4.1 双亲表示法
5.4.2 孩子链表表示法
5.5 哈夫曼树及其应用
5.5.1 最优二叉树(哈夫曼树)
5.5.1.1 哈夫曼树存储结构
5.5.1.2 选择两个最小权值根结点并返回数组下标
5.5.1.3 构造哈夫曼树算法
5.5.1.4 哈夫曼树构造实例
5.5.2 哈夫曼编码
5.5.2.1 哈夫曼编码字符集存储结构
5.5.2.2 根据哈夫曼树求哈夫曼编码表
5.5.2.3 哈夫曼编码示例
5.6 编程练习
5.6.1 习题22
5.6.2 习题23
5.6.3 习题24
5.1 二叉树
5.1.1 二叉树的链式存储结构
typedef char DataType; // 使用char来代表数据类型
typedef struct node
{DataType data;struct node *lchild, *rchild;
}BinTNode;
typedef BinTNode *BinTree;5.2 二叉树运算
5.2.1 按广义表表示二叉树结构生成二叉链表的算法
// 按广义表表示二叉树结构生成二叉链表的算法
// 参数:
// char *str str为存储广义表的字符串的指针
// 返回:
// BinTNode * 指向二叉树的指针
BinTNode *CreateTree(char *str)
{BinTNode *St[100]; // 用指针数组模拟栈BinTNode *p = NULL;int top, k = 0, j = 0;top = -1; // 置空栈char ch = str[j];BinTNode *b = NULL;while (ch != '\0'){switch (ch){case '(':top++;St[top] = p;k = 1;break;case ')':top--;break;case ',':k = 2;break;default:p = (BinTNode *)malloc(sizeof(BinTNode));p->data = ch;p->lchild = p->rchild = NULL;if (b == NULL)b = p;else{switch(k){case 1:St[top]->lchild = p;break;case 2:St[top]->rchild = p;break;}}}j++;ch = str[j];}return b;
}
int main(void)
{char *str = "(A(B(,D(E,F)),C)";BinTNode *bt = CreateTree(str);Postorder(bt);printf("\nDone.\n");return 0;
}

5.2.2 按完全二叉树的层次顺序依次输入结点信息建立二叉链表的算法
// 按完全二叉树的层次顺序依次输入结点信息建立二叉链表
// Q[1..n]是一个BinTNode类型的指针数组,front和rear分别是队头和队尾指针
// 参数:
// BinTree bt 完全二叉树
// 返回:
// BinTree 建立后的二叉链表
// 程序:
// 喻晓良
// 修改记录:
// 2022-03-12
//-----------------------------------------------------------
BinTree CreateBinTree(BinTree bt)
{BinTNode *Q[100]; // 定义队列BinTNode *s;int front, rear;char ch;ch = getchar();bt = NULL; // 置空二叉树front = 1; rear = 0; // 初始化队列while (ch != '#') // 假设结点值为单字符,#为终止符号{s = NULL;if (ch != '@'){s = (BinTNode *)malloc(sizeof(BinTNode)); // 申请结点s->data = ch; s->lchild = s->rchild = NULL; // 新结点赋值}//endif_1rear++; // 队尾指针自增Q[rear] = s; // 将新结点地址或虚结点地址(NULL)入队if (rear == 1) // 若rear为1,则说明是根结点,用bt指向它bt = s;else{if (s != NULL && Q[front] != NULL) // 当前结点及其双亲结点都不是虚结点{if (rear % 2 == 0) // rear为偶数,新结点应作为左孩子Q[front]->lchild = s;elseQ[front]->rchild = s; // rear为奇数,新结点应作为右孩子}if (rear % 2 != 0)front++; // rear为奇数,front指向下一个双亲}ch = getchar(); // 读下一个结点值} //end whilereturn bt;
}程序示例:
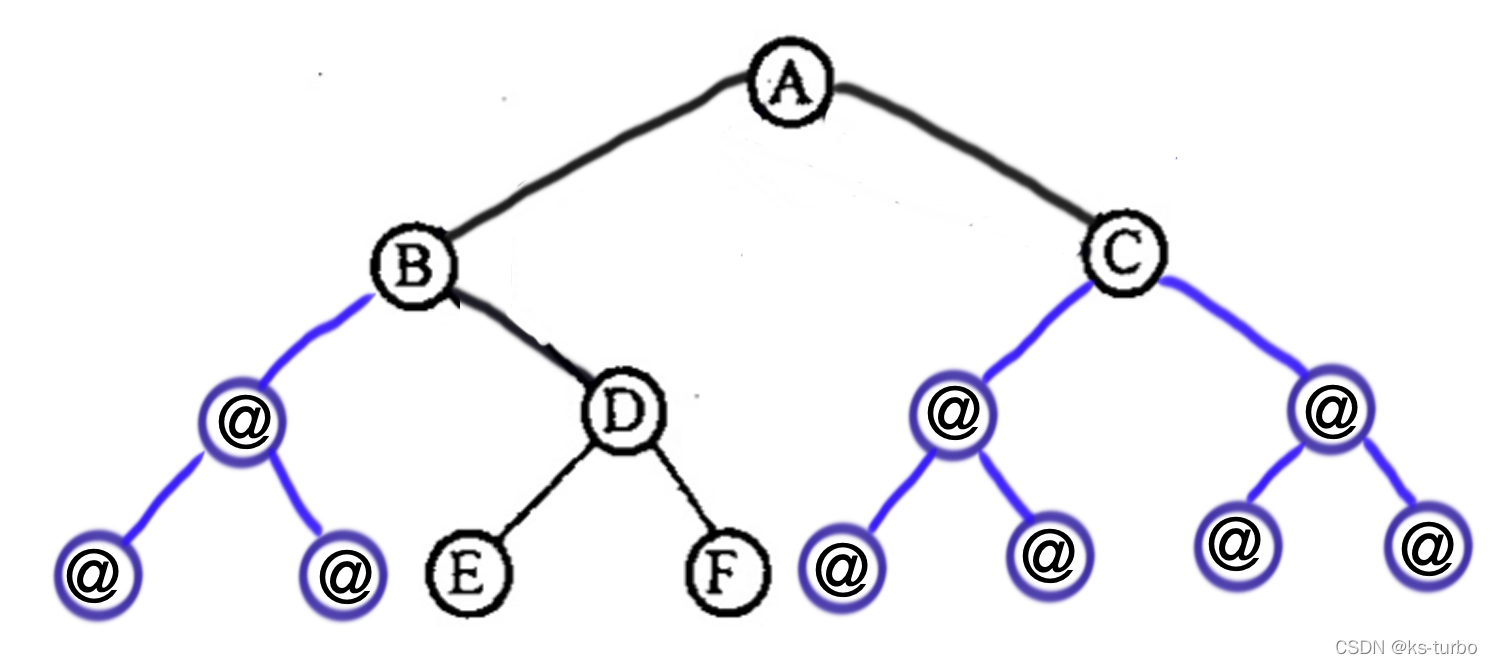
int main(void)
{BinTree bt = NULL;printf("输入完全二叉树,@表示虚结点,#表示输入完毕:\n");bt = CreateBinTree(bt);Postorder(bt);printf("\n完成.\n");return 0;
}

5.2.3 二叉树的递归遍历算法
5.2.3.1 前序遍历二叉树算法
// 前序遍历二叉树算法
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Preorder(BinTree bt)
{if (bt != NULL){printf("%c", bt->data); // 访问根结点Preorder(bt->lchild); // 前序遍历左子树Preorder(bt->rchild); // 前序遍历右子树}
}5.2.3.2 中序遍历二叉树算法
// 中序遍历二叉树算法
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Inorder(BinTree bt)
{if (bt != NULL){Inorder(bt->lchild); // 中序遍历左子树printf("%c", bt->data); // 访问根结点Inorder(bt->rchild); // 中序遍历右子树}
}5.2.3.3 后序遍历二叉树算法
// 后序遍历二叉树算法
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Postorder(BinTree bt)
{if (bt != NULL){Postorder(bt->lchild); // 后序遍历左子树Postorder(bt->rchild); // 后序遍历右子树printf("%c", bt->data); // 访问结点}
}5.2.3.4 二叉树递归便利示例

int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("前序输出二叉树:"); Preorder(bt);printf("\n中序输出二叉树:"); Inorder(bt);printf("\n后序输出二叉树:"); Postorder(bt);printf("\n");return 0;
}

5.2.4 二叉树的非递归遍历算法
5.2.4.1 利用栈的非递归中序遍历算法
// 利用栈的非递归中序遍历算法
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Inorder1(BinTree bt)
{SeqStack S;BinTNode *p;InitStack(&S);printf("入栈根结点: %c(%p)\n", bt->data, bt);Push(&S, bt);while (!IsStackEmpty(&S)){while (GetTop(&S)){printf("入栈左子树地址: %p, 值: %c\n", GetTop(&S)->lchild, ((GetTop(&S)->lchild != NULL) ? GetTop(&S)->lchild->data : ' '));Push(&S, GetTop(&S)->lchild); // 直到左子树空为止}printf("最上面一个空地址退栈\n");p = Pop(&S); // 空指针退栈if (!IsStackEmpty(&S)){printf("结点【%c】\n", GetTop(&S)->data); // 访问根结点printf("退栈地址: %p, 值: %c\n", GetTop(&S), ((GetTop(&S) != NULL) ? GetTop(&S)->data : ' '));p = Pop(&S);printf("右子树入栈地址: %p, 值: %c\n", p->rchild, ((p->rchild != NULL) ? p->rchild->data : ' '));Push(&S, p->rchild); // 右子树进栈}}
}
程序范例:

#include
#include "SeqStack.h"
#include "BinTNode.h"int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("中序非递归遍历输出二叉树:"); Inorder1(bt);printf("\n");return 0;
} 
5.2.4.2 利用栈的非递归中序遍历算法(指针数组版)
// 非递归中序遍历算法(指针数组版)
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Inorder2(BinTree bt)
{BinTNode *ST[100]; // 用指针数组模拟栈int top = 0; // 初始化数组ST[top] = bt;do{while (ST[top] != NULL) // 根结点及其所有的左结点地址装入数组{top = top + 1;ST[top] = ST[top - 1]->lchild;}top = top - 1;if (top >= 0) // 判断数组中地址是否访问完{printf("%c", ST[top]->data); // 访问结点ST[top] = ST[top]->rchild; // 扫描右子树}}while (top != -1);
}程序示例:

#include
#include "SeqStack.h"
#include "BinTNode.h"int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("中序非递归遍历输出二叉树:"); Inorder2(bt);printf("\n");return 0;
} 
5.2.4.3 利用栈的非递归前序遍历算法
// 非递归前序遍历算法(栈方法)
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Preorder1(BinTree bt)
{SeqStack S;InitStack(&S); // 初始化栈Push(&S, bt); // 根结点指针进栈while (!IsStackEmpty(&S)){bt = Pop(&S); // 出栈if (bt != NULL){printf("%c", bt->data); // 访问结点,假设数据域为字符型Push(&S, bt->rchild); // 右子树入栈Push(&S, bt->lchild); // 左子树入栈}}
}程序范例:

#include
#include "SeqStack.h"
#include "BinTNode.h"int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("前序非递归遍历输出二叉树:"); Preorder1(bt);printf("\n");return 0;
}

5.2.4.4 非递归的按层遍历二叉链表树
// 非递归按层遍历二叉链表树
// 按层遍历二叉树,从上到下,从左到右
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
void TransLevel(BinTree bt)
{CirQueue Q;InitQueue(&Q); // 初始化队列为空队列if (bt == NULL)return; // 二叉树为空,返回else{printf("%c", bt->data); // 输出根结点,假设其数据域为字符型EnQueue(&Q, bt); // 根结点入队while (!IsQueueEmpty(&Q)){bt = ExQueue(&Q); // 出队列if (bt->lchild != NULL){printf("%c", bt->lchild->data); // 输出左子树根结点EnQueue(&Q, bt->lchild); // 左子树入队列}if (bt->rchild != NULL){printf("%c", bt->rchild->data); // 输出右子树根结点EnQueue(&Q, bt->rchild); // 右子树入队列}} // end of the while} // end of the if
}程序范例:

#include
#include "SeqStack.h"
#include "CirQueue.h"
#include "BinTNode.h"int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("非递归按层遍历输出二叉树:"); TransLevel(bt);printf("\n");return 0;
}

5.2.5 综合例题
5.2.5.1 例题1 前序、中序、后续输出二叉树
分别写出如图5.12所示的二叉树的前、中、后序遍历序列。

#include
#include "SeqStack.h"
#include "CirQueue.h"int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("非递归栈方式, 前序遍历二叉树:"); Preorder1(bt);printf("\n非递归栈方式, 中序遍历二叉树:"); Inorder1(bt);printf("\n递归栈方式, 后序遍历二叉树:"); Postorder(bt);printf("\n");return 0;
} 
5.2.5.2 例题2 求二叉树深度
// 求二叉树深度的递归算法
// 若一棵二叉树为空,则它的深度为0,否则它的深度等于其左右子树中的最大深度+1
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
int BinTreeDepth(BinTree bt)
{int depl, depr;if (bt == NULL)return 0; // 对于空树,返回0,结束递归else{depl = BinTreeDepth(bt->lchild); // 计算左子树的深度depr = BinTreeDepth(bt->rchild); // 计算右子树的深度if (depl > depr)return depl + 1;elsereturn depr + 1;}
}
示例:

#include
#include "BinTNode.h"int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("二叉树深度为:%d\n", BinTreeDepth(bt));return 0;
} 
5.2.5.3 例题3 在二叉树中查询结点并计算二叉结点的层次
// 在二叉树中查找值为x的结点(前序遍历法)
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// DataType x 值为x
// 返回:
// bool 找到返回true,否则返回false
extern BinTNode *pNodeDomain;
bool FindBT(BinTree bt, DataType x)
{static bool found = false;if ((bt != NULL) && (!found)){if (bt->data == x){pNodeDomain = bt;found = true;}else{FindBT(bt->lchild, x); // 遍历查找左子树FindBT(bt->rchild, x); // 遍历查找右子树}}return found;
}// 求结点的层次
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// BinTNode *p 要找到的结点
// int lh 当前查找在第几层,初始调用从1开始
// 返回:
// int 节点所在层次
int level(BinTree bt, BinTNode *p, int lh)
{static int h = 0;if (bt == NULL) h = 0;else if (bt == p)h = lh;else{level(bt->lchild, p, lh + 1);if (h == 0) // 表示左子树已查完level(bt->rchild, p, lh + 1);}return h;
}
程序示例:

#include
#include "BinTNode.h"BinTNode *pNodeDomain;int main(void)
{BinTree bt = NULL;char ch;int lh = 0;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);//不停地使用getchar()获取缓冲中字符,直到获取的c是“\n”或文件结尾符EOF为止while ((ch = getchar()) != EOF && ch != '\n');printf("输入要查找的值:"); scanf("%c", &ch);if(FindBT(bt, ch)){lh = 1;printf("找到了结点,节点值为:%c,节点的层次为:%d\n",pNodeDomain->data, level(bt, pNodeDomain, lh));}elseprintf("没有查询到.\n");return 0;
} 
5.3 线索二叉树
5.3.1 二叉树的线索化
5.3.1.1 二叉链表加中序线索
// 对以根结点指针为bt的二叉链表树加中序线索的算法
// 参数:
// BinThrTree bt 二叉线索根结点
// 返回:
// void
void InorderThread(BinThrTree bt)
{static BinThrNode *pre = NULL;if (bt != NULL) // 当二叉树为空时结束递归{InorderThread(bt->lchild); // 左子树线索化if (bt->lchild == NULL)bt->ltag = 1;elsebt->ltag = 0;if (bt->rchild == NULL)bt->rtag = 1;elsebt->rtag = 0;if (pre){if (pre->rtag == 1) // 给前趋结点加后继线索pre->rchild = bt;if (bt->ltag == 1) // 给当前结点加前趋线索bt->lchild = pre;}pre = bt; // 将刚访问过的当前结点置为前趋结点InorderThread(bt->rchild); // 右子树线索化}
}程序示例:

#include
#include "BinThrTree.h"int main(void)
{BinThrTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("构造二叉树完成,开始加中序索引...\n");InorderThread(bt);printf("中序索引完成,开始输出二叉线索树...\n");TinorderThrTree(bt);return 0;
}
代码中使用到5.3.2.1的程序段和5.3.2.2的程序段。见下文。

5.3.2 二叉线索链表上的运算
5.3.2.1 查找某结点*p的后继结点
// 中序线索二叉树上求结点*p的中序后继结点
// 参数:
// BinThrNode *p 节点*p
// 返回:
// BinThrNode 后继结点
BinThrNode *InorderNext(BinThrNode *p)
{if (p->rtag == 1) // rchild域为右线索return p->rchild; // 返回中序后继结点指针else{p = p->rchild; // 从*p的右孩子开始while (p->ltag == 0)p = p->lchild; // 沿左指针向下查找return p;}
}5.3.2.2 线索二叉树的遍历
// 遍历以bt为根结点指针的中序线索二叉树
// 参数:
// BinThrTree bt 以bt为根结点指针的中序线索二叉树
// 返回:
// void
void TinorderThrTree(BinThrTree bt)
{BinThrNode *p;if (bt != NULL) // 二叉树不为空{p = bt; // 使p指向根结点while (p->ltag == 0)p = p->lchild; // 查找出中序遍历的第一个结点do{printf("[%c <- %d ",(p->lchild == NULL ? ' ' : p->lchild->data),p->ltag);printf("%c", p->data); // 输出访问结点值printf(" %d -> %c]\n", p->rtag,(p->rchild == NULL ? ' ' : p->rchild->data));p = InorderNext(p); // 查找结点*p的中序后继结点}while (p != NULL); // 当p为空时算法结束}
}
5.4 数和森林
5.4.1 数的存储结构
5.4.1 双亲表示法

#define MaxTreeSize 100
typedef char DataType;typedef struct
{DataType data; // 树结点数据域int parent; // 双亲位置域
} PTNode;typedef struct
{PTNode nodes[MaxTreeSize];int n; // 结点数
}PTree;5.4.2 孩子链表表示法

#define MAXTreeSize 100
typedef char DataType;
typedef struct cnode // 孩子链表结点类型
{int child; // 孩子结点在指针数组中的序号struct cnode *next;
}CNode;typedef struct
{DataType data; // 树中结点数据域CNode *firstchild; // 孩子结点头指针
}PANode; // 指针数组结点类型typedef struct
{PANode nodes[MAXTreeSize]; // 指针数组int n, r; // n为结点数, r为根结点在指针数组中的位置(即下标)
}CTree;5.5 哈夫曼树及其应用
5.5.1 最优二叉树(哈夫曼树)
5.5.1.1 哈夫曼树存储结构
#define n 100 // 叶子结点数
#define m 2 * n - 1 // 哈夫曼树中结点总数
typedef struct
{float weight; // 权值int lchild, rchild, parent; // 左右孩子及双亲指针
}HTNode; // 树中结点类型
typedef HTNode HuffmanTree[m + 1]; // 0号单元不用
5.5.1.2 选择两个最小权值根结点并返回数组下标
// 在HT[1..k]中选择parent为0且权值最小的两个根结点
// 其序号分别存储在s1和s2指向的对应变量中
// 参数:
// HuffmanTree HT 一维数组形式的哈夫曼树
// int k 数组下标的最大范围
// int *s1 返回的最小值下标
// int *s1 返回的次最小值下标
// 返回:
// void
void SelectMinItem(HuffmanTree HT, int k, int *s1, int *s2)
{if (k < 2) return;const float MAX_VALUE = 65535.0;int i, j;float min = MAX_VALUE;// 取最小权值for (i = 1; i <= k; i++){if (HT[i].weight < min && HT[i].parent == 0){j = i;min = HT[i].weight;}}*s1 = j;//取次最小权值min = MAX_VALUE;for (i = 1; i <= k; i++){if (HT[i].weight < min && HT[i].parent == 0 && i != *s1){j = i;min = HT[i].weight;}}*s2 = j;
}5.5.1.3 构造哈夫曼树算法
// 创建哈夫曼树
// 参数:
// HuffmanTree HT 一维数组形式的哈夫曼树
// 返回:
// void
void CreateHuffmanTree(HuffmanTree HT)
{int i;int s1, s2;for (i = 1; i <= m; i++) // 初始化哈夫曼树{HT[i].lchild = 0;HT[i].rchild = 0;HT[i].parent = 0;HT[i].weight = 0;}for (i = 1; i <= n; i++) // 输入前n个叶结点的权值scanf("%f", &HT[i].weight);for (i = n + 1; i <= m; i++) // 在HT[1..i-1]中选择parent为0且权值最小的两个根结点,序号分别为s1和s2{select(HT, i - 1, &s1, &s2);HT[s1].parent = i;HT[s2].parent = i;HT[i].lchild = s1;HT[i].rchild = s2;HT[i].weight = HT[s1].weight + HT[s2].weight; // 权值之和}
}
5.5.1.4 哈夫曼树构造示例
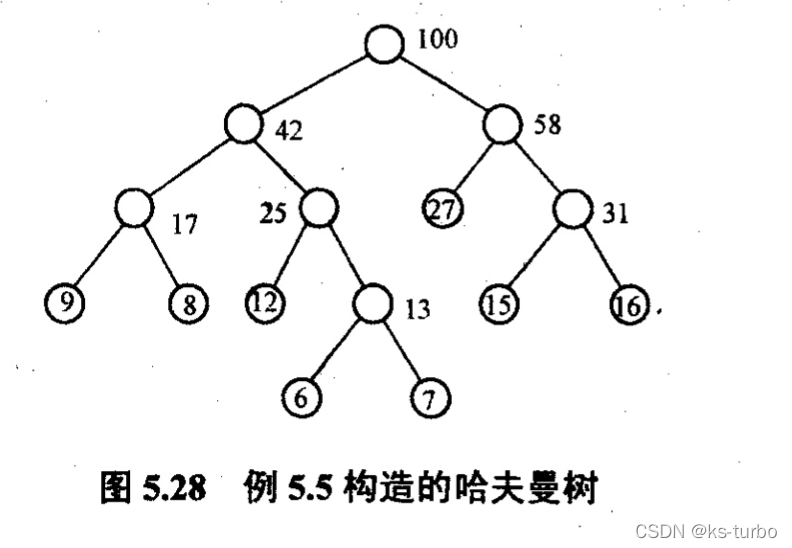
#include
#include "HuffmanTree.h"int main(void)
{HuffmanTree ht;printf("开始输入8个权值:");CreateHuffmanTree(ht);return 0;
}

5.5.2 哈夫曼编码
5.5.2.1 哈夫曼编码字符集存储结构
typedef struct
{char ch; // 存放编码的字符char bits[n + 1]; // 存放编码的位串int len; // 编码长度
}CodeNode;
typedef CodeNode HuffmanCode[n + 1];
5.5.2.2 根据哈夫曼树求哈夫曼编码表
// 依据哈夫曼树HT求哈夫曼编码表
// 参数:
// HuffmanTree HT 一维数组形式的哈夫曼树
// HuffmanCode HC 返回哈夫曼编码表
// 返回:
// void
void HuffmanEncoding(HuffmanTree HT, HuffmanCode HC)
{int c, p , i; // c和p分别指示HT中孩子和双亲的位置char cd[n + 1]; // 临时存放编码串int start; // 指示编码在cd中的起始位置cd[n] = '\0'; // 最后一位放上串结束符for (i = 1; i <= n; i++){start = n; // 初始位置c = i; // 从叶子结点HT[i]开始上溯HC[i].ch = HT[i].ch; // 复制字符while ((p = HT[c].parent) > 0) // 直到上溯到ht[c]是树根为止{// 若HT[c]是HT[p]的左孩子,则生成代码0,否则生成代码1cd[--start] = (HT[p].lchild == c) ? '0': '1';c = p;} // end of whilestrcpy(HC[i].bits, &cd[start]); // 将临时串cd中的编码拷贝到编码表中HC[i].len = n - start; // 保存编码长度} // end of for
}5.5.2.3 哈夫曼编码示例

#include
#include "HuffmanCode.h"int main(void)
{int i, j;HuffmanTree HT;HuffmanCode HC;printf("输入8个字母和对应的权值:\n");CreateHuffmanTree(HT);HuffmanEncoding(HT, HC);printf("输出哈夫曼树的权:\n");for (int i = 1; i <= m; i++)printf("%4.0f", HT[i].weight);printf("\n输出哈夫曼编码表:\n");for (i = 1; i <= n; i++){printf("字符:%2c 权值:%3.0f 长度:%2d 编码为: ", HC[i].ch, HT[i].weight, HC[i].len);for (j = 0; j <= n; j++){if(HC[i].bits[j] == '\0') break;printf("%2c", HC[i].bits[j]);}printf("\n");}return 0;
} 
5.6 编程练习
5.6.1 习题22
以二叉链表作为存储结构,试利用指针数组实现编写非递归的前序遍历二叉树的算法。

// 非递归前序遍历算法(指针数组版)
// 参数:
// BinTree bt 采用二叉树链表存储结构,并设结点值为字符型
// 返回:
// void
void Preorder2(BinTree bt)
{BinTNode *ST[100]; // 用指针数组模拟栈int top = 0; // 初始化数组ST[top] = bt;do{while (ST[top] != NULL) // 根结点及其所有的左结点地址装入数组{printf("%c", ST[top]->data); // 访问结点top = top + 1;ST[top] = ST[top - 1]->lchild;}top = top - 1;if (top >= 0) // 判断数组中地址是否访问完{ST[top] = ST[top]->rchild; // 扫描右子树}}while (top != -1);
}程序示例:
int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("非递归指针数组方式, 前序遍历二叉树:"); Preorder2(bt);printf("\n");return 0;
}
5.6.2 习题23
以二叉链表作为存储结构,其根结点指针为bt,试写从根开始按层遍历二叉树的算法。
此题可使用前文提到的按层输出二叉树函数。
示例程序如下:

int main(void)
{BinTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("非递归按层遍历输出二叉树:"); TransLevel(bt);printf("\n");return 0;
}

5.6.3 习题24
以中序线索二叉树作为存储结构,试写查找某结点*p的中序前缀结点的算法。

// 中序线索二叉树上求结点*p的中序前趋结点
// 参数:
// BinThrNode *p 节点*p
// 返回:
// BinThrNode 后继结点
BinThrNode *InOrderPre(BinThrNode *p)
{if (p->ltag == 1) // lchild域为左线索return p->lchild; // 返回中序前趋结点指针else{p = p->lchild; // 从*p的左孩子开始if(p->rtag == 0) // 如果左孩子存在一个右孙子,则使用右孙子返回p = p->rchild;else if(p->ltag == 0) // 没有右孙子则使用左孙子返回p = p->lchild;return p;}
}程序示例:
#include
#include "BinThrTree.h"int main(void)
{BinThrTree bt = NULL;printf("使用完全二叉树构建,@表示虚结点,#结束输入:\n");bt = CreateBinTree(bt);printf("构造二叉树完成,开始加中序索引...\n");InorderThread(bt);printf("中序索引完成,开始输出二叉线索树...\n");TinorderThrTree(bt);return 0;
}

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!