不定期备考小tips[常微][0] #20210524

不定期备考小tips[常微][0] #20210524

• 常微（Strogatz书）
• • 一些描述稳定性的词汇
  • 退化结点(degenerate node)
  • 线性近似
  • 换极坐标常见套路
  • 关于对称性的若干思考

本专栏主要作个人笔记，有相关知识预备的同学也可作复习用。不保证无相应基础的人士能看明白。
万一考试考到了，或者对你的学习有较大帮助，一键三连不过分吧（斜眼笑）

常微（Strogatz书）

参考书籍：

一些描述稳定性的词汇

假设 x ⃗ 0 = 0 ⃗ \vec x_0 = \vec 0 x 0​=0 是待考察的点。

1. 吸引的(attracting)
   $t\to \infty$时，一切 0 ⃗ \vec 0 0 附近的点都演化到 0 ⃗ \vec 0 0 处。（特别地，如果不仅仅是“附近”，而是所有点，就称为全局吸引的(globally attracting）。
2. 李雅普诺夫稳定(Liapunov stable)
   任意 0 ⃗ \vec 0 0 附近小球 B ϵ ( 0 ) B_\epsilon(0) Bϵ​(0)，都可以找到相应的 0 ⃗ \vec 0 0 附近小球 B δ ( 0 ) B_\delta(0) Bδ​(0)（$\delta$当然和$ϵ$有关），使得 B δ ( 0 ) B_\delta(0) Bδ​(0)当中起始的轨迹在演化中都不超出小球 B ϵ ( 0 ) B_\epsilon(0) Bϵ​(0)
3. 两者的区别和联系
   李雅普诺夫稳定但不吸引称为中性稳定。(neutrally stable)，两者都满足称为渐近稳定/稳定(asymptotically stable/stable)，两者都不满足称为不稳定(unstable)。
4. 两者互不蕴含。反例：

• 圆环上（即$x=0$和$x=2\pi$看作相同的点）， x ˙ = 1 − c o s x \dot x = 1-cosx x˙=1−cosx决定的系统。原点处吸引但不李雅普诺夫稳定。
  思考：如果需要构造二维平面上类似于上述性质的系统，怎么办？一种可能的做法是直接令二维平面上一个环形处的向量场 x ⃗ \vec x x 大小由上面决定，而方向由圆环的切向决定。其它地方就连续作延拓。
• 每一点都有 x ⃗ ˙ = 0 \dot{ \vec x} = 0 x ˙=0决定的系统。任意点处李雅普诺夫稳定但不吸引。
• 二维平面上所有点都趋向于$x$轴的系统。（一 向 箔）

退化结点(degenerate node)

二维系统，平衡点附近矩阵的Jordan标准形如 ( λ 1 0 λ ) , λ ≠ 0 \left(\begin{matrix}\lambda & 1 \\ 0 & \lambda\end{matrix}\right),\lambda \neq 0 (λ0​1λ​),λ​=0，则是退化结点。（如果$\lambda =0$则是非孤立结点！）

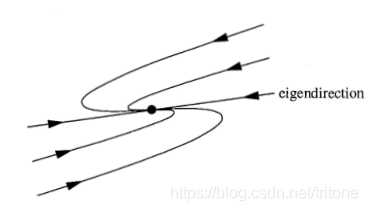
1. 理解方式1： ( 1 , 0 ) T (1, 0)^T (1,0)T是原矩阵特征向量，则看到直线（图中eigendirection），而一般的 ( c o s θ , s i n θ ) T (cos\theta,sin\theta)^T (cosθ,sinθ)T不是，且
   ( λ 1 0 λ ) ( c o s θ s i n θ ) = ( λ c o s θ + s i n θ λ s i n θ ) \left(\begin{matrix}\lambda & 1 \\ 0 & \lambda\end{matrix}\right) \left(\begin{matrix}cos\theta \\ sin\theta \end{matrix}\right)= \left(\begin{matrix}\lambda cos\theta + sin\theta \\ \lambda sin\theta \end{matrix}\right) (λ0​1λ​)(cosθsinθ​)=(λcosθ+sinθλsinθ​)
   可以看到$\theta$从$0$变化到$\pi /2$时， ( λ c o s θ + s i n θ λ s i n θ ) \left(\begin{matrix}\lambda cos\theta + sin\theta \\ \lambda sin\theta \end{matrix}\right) (λcosθ+sinθλsinθ​)的变化情况解释了图。（关键点是每个点唯一决定了一个方向。如果决定的方向恰好指向平衡点就是星(star)。而此处决定的方向不恰好指向平衡点）
2. 理解方式2： ( λ 1 0 λ ) \left(\begin{matrix}\lambda & 1 \\ 0 & \lambda\end{matrix}\right) (λ0​1λ​)中左上角的$\lambda$做微扰，退化结点将被扰动成具有两个非常相近的特征方向的结点，且两个特征方向衰减一快一慢。
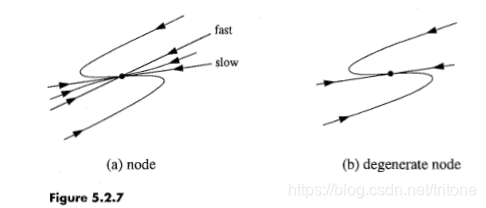
3. 理解方式3：介于螺旋(spiral)与结点(node)之间。（方程的两根从两个相近的实根过渡到两个相近的共轭复根）
   个人认为前两种理解方式更合理，因为是否是退化结点不光是方程两根决定的，而是和对角化有关。这里的“方程的根过渡”难以解释什么时候是星(star)，什么时候是退化结点。

线性近似

1. 对于一般的平衡点 ( x ⋆ , y ⋆ ) (x^\star, y^\star) (x⋆,y⋆)，我们换元 u = x − x ⋆ , v = y − y ⋆ u=x-x^\star,v=y-y^\star u=x−x⋆,v=y−y⋆，则$u,v$在原点附近的行为就可近似用一阶线性常系数微分方程组
   ( u ˙ v ˙ ) = A ( u v ) \left(\begin{matrix}\dot u \\ \dot v\end{matrix}\right)=A \left(\begin{matrix}u \\ v \end{matrix}\right) (u˙v˙​)=A(uv​)
   刻画。我们舍去了二阶以上的项。
2. 如此近似考察下如果该平衡点不是边界情况（也就是该点是鞍点、结点或螺旋），则可以确定未近似也如此。特别注意星是边界情况。
   其它边界情况：退化结点，中心，非孤立的平衡点。
   星和退化结点在扰动下稳定性不变，只是“性质”可能改变。
   这其实从高层次来讲就是个分类标准问题。比如你可以把所有稳定平衡点都分为一类，那么星和退化结点就不是边界情况。或者你可以把附近存在与 y = x 520 y=x^{520} y=x520图像某局部全等的轨迹的结点称为“虐狗结点”，那么“虐狗结点”显然在高阶扰动下可能改变其“性质”。什么叫做一类，什么叫做“性质”，什么叫做“边界”凭你喜欢。
   实际上，书154页有个采用另一种标准的分类：即

• 鲁棒(Robust)情况：源(source)，汇(sink)，鞍点(saddle)。
• 边界(Marginal)情况：中心(center)，非孤立(non-isolated)。
  此处“鲁棒”表示“参数”扰动下，平衡点类型的某种“稳定性”。而“稳定”本身表示待考察变量 x ⃗ \vec x x 被扰动后在之后演化中的稳定性。老套娃了！

3. 做例题 x ˙ = − x + x 3 , y ˙ = − 2 y \dot x=-x+x^3, \dot y=-2y x˙=−x+x3,y˙​=−2y：先画出平衡点，再画出水平竖直线（特征方向），再画其它线。
4. 做例题 x ˙ = − y + a x ( x 2 + y 2 ) , y ˙ = x + a y ( x 2 + y 2 ) \dot x=-y+ax(x^2+y^2), \dot y=x+ay(x^2+y^2) x˙=−y+ax(x2+y2),y˙​=x+ay(x2+y2)
   直接舍去非线性项，发现是边界情况（中心）。
   近似后是中心，实际可能不是中心，而是稳定螺旋或不稳定螺旋。（可类比一维 x ˙ = x 3 \dot x = x^3 x˙=x3）
   看到 x 2 + y 2 x^2+y^2 x2+y2，尝试换极坐标，发现就很容易考察。

换极坐标常见套路

这个是个比较普遍的技巧，值得开个小标题。

1. 从 x 2 + y 2 = r 2 x^2+y^2=r^2 x2+y2=r2得到 x x ˙ + y y ˙ = r r ˙ x\dot x+y\dot y=r\dot r xx˙+yy˙​=rr˙
2. 从$rcos\theta =x,rsin\theta =y$得到
   r c o s θ θ ˙ = y ˙ − r ˙ s i n θ , r s i n θ θ ˙ = − x ˙ + r ˙ c o s θ rcos\theta \dot\theta=\dot y -\dot rsin\theta, rsin\theta \dot \theta =- \dot x +\dot rcos\theta rcosθθ˙=y˙​−r˙sinθ,rsinθθ˙=−x˙+r˙cosθ
   x 2 θ ˙ = x y ˙ − x r ˙ s i n θ , y 2 θ ˙ = − y x ˙ + y r ˙ c o s θ x^2\dot \theta=x\dot y-x\dot r sin\theta, y^2\dot\theta=-y\dot x+y\dot rcos\theta x2θ˙=xy˙​−xr˙sinθ,y2θ˙=−yx˙+yr˙cosθ
   在一切 x 2 + y 2 ≠ 0 x^2+y^2\neq 0 x2+y2​=0也就是$r\ne 0$的点，两式相加得到
   θ ˙ = x y ˙ − y x ˙ r 2 \dot \theta = \frac{x\dot y -y \dot x}{r^2} θ˙=r2xy˙​−yx˙​
   （直接假定 a r c t a n y x arctan\frac yx arctanxy​存在当然是不严谨的，但可以帮助记忆）

关于对称性的若干思考

x ˙ = y , y ˙ = − x \dot x= y,\dot y = - x x˙=y,y˙​=−x，直接通过对称性证明有闭轨。

1. 关于对称性的简单理解：进行某些变换之后，系统不变（在此处可理解为只有变量名不同）。

• 轴对称：关于某直线反射下不变。
  具体地：平面图形看成一些$(x,y)$构成的点集，那么关于$y$轴轴对称，也就是点集 { ( x , y ) ∣ ( x , y ) ∈ A } = { ( x ′ , y ) ∣ ( x ′ , y ) ∈ A } \{(x,y)|(x,y)\in A\}=\{(x',y)|(x',y)\in A\} {(x,y)∣(x,y)∈A}={(x′,y)∣(x′,y)∈A}，其中 x ′ = − x x'=-x x′=−x。换元了之后，只有变量名不同，表示的仍是一个点集。
• 中心对称：绕某点旋转一定角度不变。
• 时间平移对称性：所有时间$t$换成 t + t 0 t+t_0 t+t0​，不变
• 空间平移对称性：所有空间$x$换成 x + x 0 x+x_0 x+x0​，不变
• 时间反演对称性：所有时间$t$换成$-t$，不变

2. 本系统具有的对称性

• 显然关于原点旋转任意角度，系统不变。但实际上满足此性质的系统还有决定各种螺旋线的系统。所以仅用该对称性不够。
• 整个系统放大， x ′ = a x , y ′ = a y x'=ax,y'=ay x′=ax,y′=ay，系统不变（即 x ˙ ′ = y ′ , y ˙ ′ = − x ′ \dot x' = y', \dot y' = -x' x˙′=y′,y˙​′=−x′，系统只有变量名不同）。
  但实际上满足此性质的系统还有决定对数螺线的系统等。
• 时间反演同时关于一条直线对称， t ′ = − t , x ′ = − x , y ′ = y t'=-t, x'=-x, y'=y t′=−t,x′=−x,y′=y，系统不变（即 d x ′ d t ′ = y ′ , d y ′ d t ′ = − x ′ \frac{dx'}{dt'}=y',\frac{dy'}{dt'}=-x' dt′dx′​=y′,dt′dy′​=−x′，系统只有变量名不同）。
  该对称性可以证明系统具有闭轨。因为$(0,1)$（时间上正向）运动到$y$负半轴和时间反演到$y$轴负半轴到达的点相同。
  然而此时并没有证明到达的点纵坐标$-1$。实际上，此时再加上旋转对称性就可以说明这一点。
  设$(0,1)$运动到$x$轴为$A$点，时间反演到$x$轴为$B$点，则$A$与$B$关于原点对称。则$A$和$B$各自再运动到$y$轴处，两点仍对称。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！