C++实现 质因数分解、最大公约数、最小公倍数、求所有因数

C++实现 质因数分解、最大公约数、最小公倍数、求所有因数

• • 一、质因数分解（包含重复的质因子）
  • 二、质因数分解（不包含重复的质因子）
  • 三、最大公因数
  • 四、最小公倍数
  • 五、求某个数x的所有因子
  • • 暴力递归
    • 动态规划

一、质因数分解（包含重复的质因子）

如：12 = 2x2x3
8 = 2x2x2
1既不是质数也不是合数
以下四种求解质因数的方法，都用统一的接口：

//分解的质因数，从小到大，存储在数组 primeFactors 中
static void getPrimeFactors(long x, vector<long> & primeFactors)

前三种方法统一的思路：
（1）p从2到x的范围上遍历，先找到x的最小质因子p
（2）当x == p时，已经找完所有的质因子
（3）当x > p时， x /= p，回到（1）
第四种方法是：在[2,p]的范围上，找到x的最小因子p，p一定是质数，然后不断的用x/=p，把x中的p因子都获得。再去找下一个质因子。

方法1（递归）
举例子：
（1）先找到12的最小质因子 2， 12 > 2，进入递归
（2）然后，找12/2 = 6，的最小质因子 2， 6 > 2, 进入递归
（3）然后，找6/2 = 3, 的最小质因子 3， 3 == 3, 3本身就是质数了

static void getPrimeFactors(long x, vector<long> & primeFactors) {if (x == 1) return;long p = 2;//找从2开始第一个可以整除x的整数，这个数一定是x的最小质因数for (p = 2; p <= x; p++) {if (x % p == 0)break;}primeFactors.push_back(p);//如果这个数等于x，说明x只有自己一个大于1的因数，x是质数if (x == p)return;//递归getPrimeFactors(x/p, primeFactors);
}

方法2（非递归，沿用上面递归的思想，改写为非递归的形式）

static void getPrimeFactors2(long x, vector<long> & primeFactors) {long p = 2;while (x != 1) {for (p = 2; p <= x; p++) {if (x % p == 0)break;}primeFactors.push_back(p);x /= p;}
}

方法3 （只用1层循环）
需要在找到x的最小质因数p后，将p重置为2

static void getPrimeFactors3(long x, vector<long> & primeFactors) {long p = 2;//假设，原数已经找到了质因数（从小到大排列，包含重复值）p1,p2,...,pt//此时 x = x/(p1*p2*...*pt);//在[2，x]的区间内，寻找x的最小质因数while (p <= x) {if (x % p == 0) {//找到了x的最小质因数pprimeFactors.push_back(p);if (x == p)break;x /= p;p = 2;}else p++;}
}

方法4

static void getPrimeFactors4(long x, vector<long> & primeFactors) {long p = 2;for (p = 2; p <= x; p++) {//找到x的一个质因子p之后，就不断的除以p,找到x中到底有多少个p。while (x % p == 0) {primeFactors.push_back(p);if (x == p)return;x /= p;}}
}

二、质因数分解（不包含重复的质因子）

如果，题目要求得到不包含重复的质因子
用方法3，稍作改动，可以很容易得到解
即，在找到x的最小质因子后，不将p重置为2
但是，需要判断p是否为质数
举例子：x0 = 24
（1）首先在[2，24]区间，找到了x0的最小质因子2
（2）x1 = x0/2 = 12, 在[3, 12]区间，找到x1的最小质因子3
（3）x2 = x1/3 = 4, 在[4, 4]区间，找到了x2的因子4，但4不是质数，之后p=5, p>x2，结束循环

static bool isPrime(long x) {for (long p = 2; p < x; p++) {if (x % p == 0)return false;}return true;
}static void getPrimeFactorsNoRepeat(long x, vector<long> & primeFactors) {long p = 2;//假设，原数已经找到了质因子（从小到大排列，不包含重复值）p1,p2...,pt//此时，x = x/(p1*p2*...*pt);//在[pt+1, x]的范围上，找x的最小质因数while (p <= x) {if (x % p == 0 && isPrime(p)) {primeFactors.push_back(p);if (x == p)return;x /= p;}p++;}
}

用方法4得到不包含重复质因数的解

static void getPrimeFactors4(long x, vector<long> & primeFactors) {long p = 2;bool flag = true;for (p = 2; p <= x; p++) {//找到x的一个质因子p之后，就不断的除以p,但是只记录1次p。while (x % p == 0) {if (flag) {primeFactors.push_back(p);flag = false;}if (x == p)return;x /= p;}flag = true;}
}

三、最大公因数

最朴素的方法：
找到每个数的所有因子，然后找到公共因子中，最大的。
如：
12的因子：1,2,3,4,6,12
18的因子：1,2,3,6,9,18
时间复杂度：在于如何求每个数的所有公因子？如果是遍历[1,x]区间，那么复杂度是O(N1+N2)？

抛开求所有因子的思路。
对每一个数，分别得到质因数分解，最大公约数可以通过两组质因数分解的交集求得。
比如：
60 = 2x2x3x5
140 = 2x2x5x7
60和140的质因数为：2x2x5

static long getGreatestCommonFactor(long x1, long x2) {vector<long> vec1;vector<long> vec2;getPrimeFactors4(x1, vec1);getPrimeFactors4(x2, vec2);int p1 = 0;int p2 = 0;long res = 1;while (p1 < vec1.size() && p2 < vec2.size()) {if (vec1[p1] == vec2[p2]) {res *= vec1[p1];p1++;p2++;}else if (vec1[p1] < vec2[p2]) {p1++;}else {p2++;}}return res;
}

四、最小公倍数

求两个整数的质因数分解的，并集
12 = 2x2x3
40 = 2x2x2x5
最小公倍数：2x2x2x3x5

static long getLeastCommonMultiple(long x1, long x2) {vector<long> vec1;vector<long> vec2;getPrimeFactors4(x1, vec1);getPrimeFactors4(x2, vec2);int p1 = 0;int p2 = 0;long res = 1;while (p1 < vec1.size() && p2 < vec2.size()) {if (vec1[p1] == vec2[p2]) {res *= vec1[p1];p1++;p2++;}else if (vec1[p1] < vec2[p2]) {res *= vec1[p1];p1++;}else {res *= vec2[p2];p2++;}}while (p1 < vec1.size()) {res *= vec1[p1];p1++;}while (p2 < vec2.size()) {res *= vec2[p2];p2++;}return res;
}

五、求某个数x的所有因子

通过分解质因数，来求。
先求质因数分解，再求所有的因子，怎么得到所有的因子？组合数的问题，比如：2个2, 3个3,1个7, 能得到多少个因子？
2个2， 3个3， 1个7
2,2,3,3,3,7
首先：
由0个质因子组成，1种
由1个质因子组成，3种
由2个质因子组成，第一个质因子选2，那么第二个质因子的选择有3种；第一个质因子选3，那么第二个质因子的选择有3种；第一个质因子选7，第二个质因子的选择有2种。重复计算了23，27，37这三个
由3个质因子组成，
…
上面这个思路，太繁琐了，解不出来了。
后来，看到一篇博客，才幡然醒悟，原来高中数学课本讲过这种问题：2^2 * 3^3 * 7 的因子 ，一定是 2^a * 3^b * 7^c的形式。其中a,b,c的选择，分别有3种，4种和2种。
所以如下，756的所有因子，就是下面(ii)式展开之后，得到的每一项。

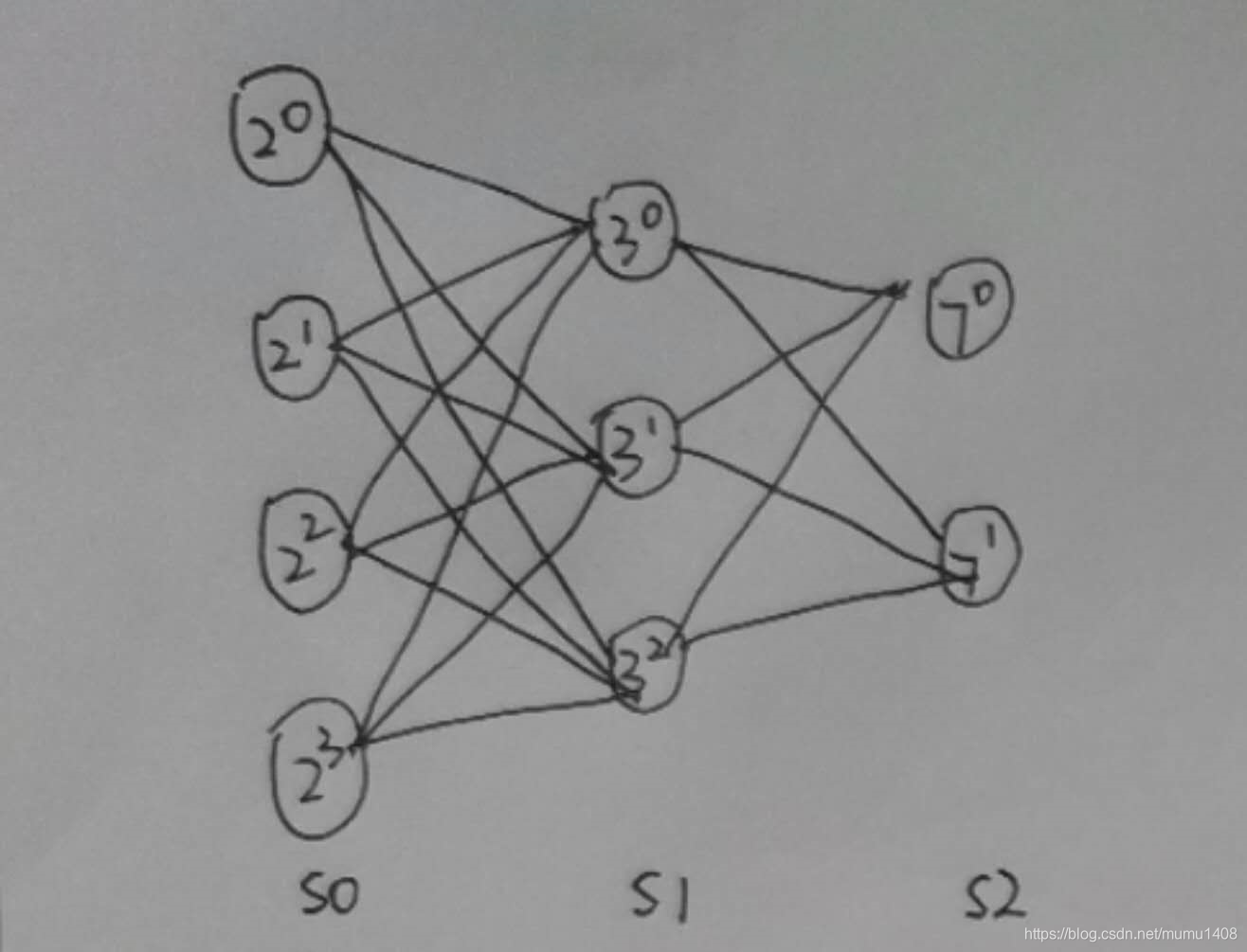
由上面的分析，可知，在已知某个数的质因数分解，求其所有因子的过程，就是求下图的每条路径的乘积。
可以由暴力递归，或者是动态规划求解。

暴力递归

//暴力递归的方法
static void process(int t, vector<vector<long>> & primeFactors, long path, vector<long> & factors) {if (t == primeFactors.size()) {factors.push_back(path);return;}long count = primeFactors[t][1];long p = primeFactors[t][0];for (int i = 0; i <= count; i++) {process(t+1, primeFactors, path*pow(p, i), factors);}
}static vector<long> getAllFactors(long x) {vector<vector<long>> primeFactors = getPrimeFactors(x);vector<long> factors;//{2:2}//{3:3}//{7:1}process(0, primeFactors, 1, factors);return factors;
}

如下所示，每条路径，需要计算2次乘法。总共需要4x3x2x2 = 48次乘法。
注意：在计算2^0 * 3^0 * 7^0 和 计算 2^1 * 3^0 * 7^0 时，会有重复计算。

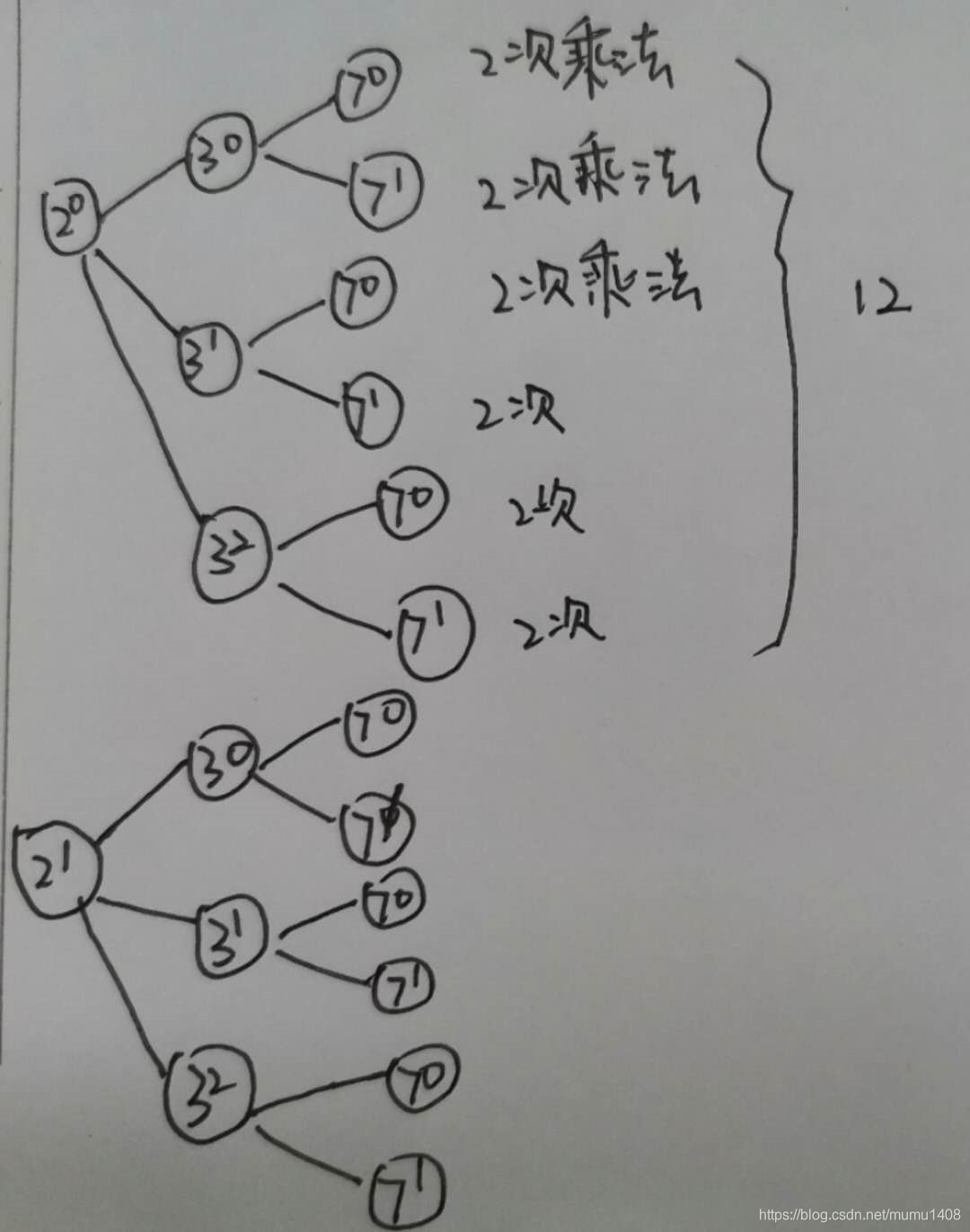
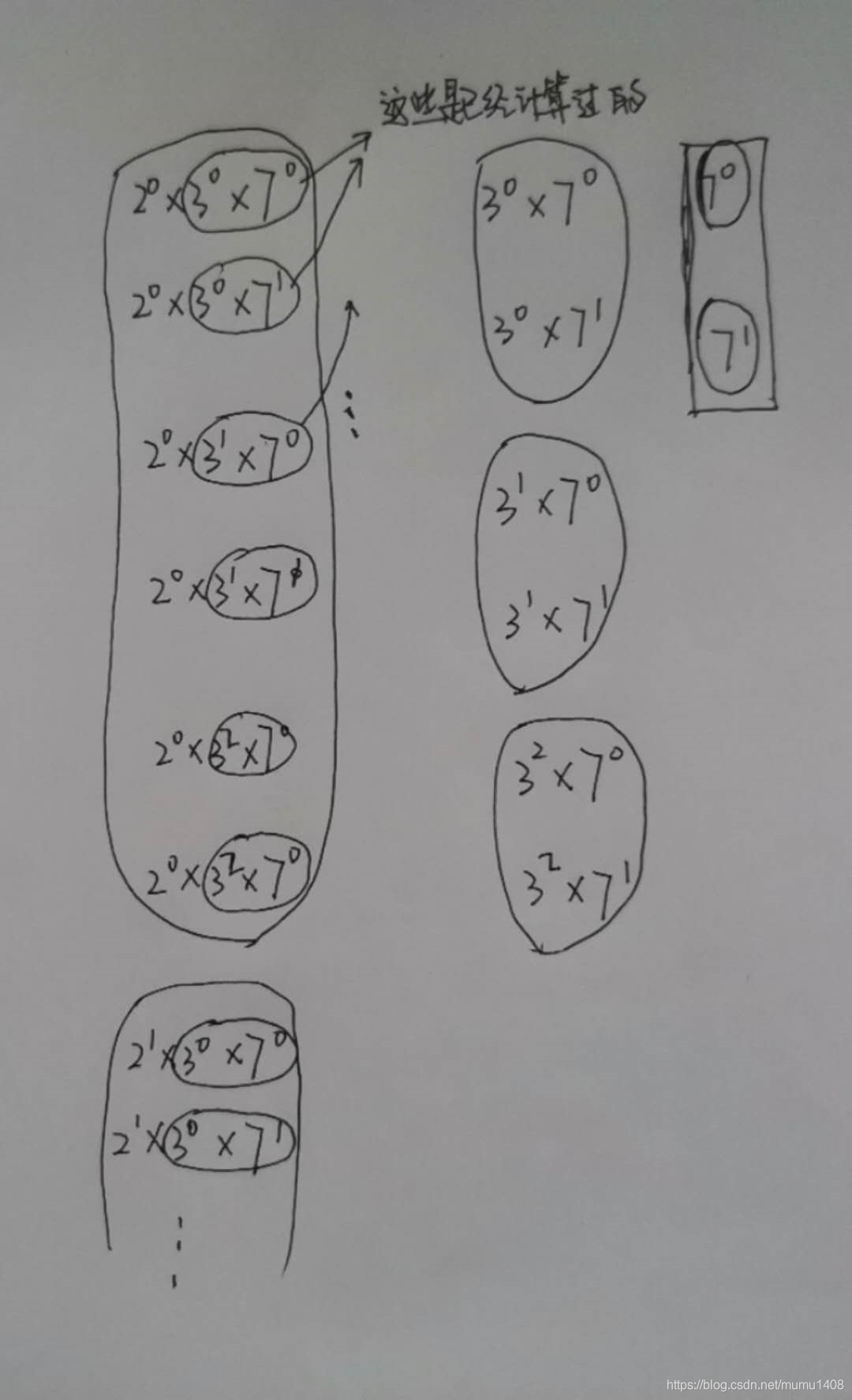
动态规划

先得到s3阶段，结果为1
再得到s2阶段，结果为[1, 7]
再得到s1阶段，结果为[1, 7, 3, 21, 9, 54]
最后得到s0阶段，结果为[1, 7, 3, 21, 9, 54, 2*(1, 7, 3, 21, 9, 54), …]
需要的乘法计算有：2 + 3x2 + 4x(3x2)

static vector<long> getAllFactorsDP(long x) {vector<vector<long>> primeFactors = getPrimeFactors(x);vector<long> factors;int size = primeFactors.size();vector<vector<long>> dp(size+1);dp[size].push_back(1);for (int i = size-1; i >= 0; i--) {vector<long> tmp = dp[i+1];long p = primeFactors[i][0];long count = primeFactors[i][1];for (int j = 0; j <= count; j++) {for (long path : tmp) {dp[i].push_back(path * pow(p, j));}}}return dp[0];
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！