【文献阅读】AlphaStock

AlphaStock

1 研究动机是什么？

传统的 QT（quantitative trading）策略通常是基于某种特定的金融逻辑，只能利用金融市场中的某些特定的特征，因此很容易受到不同状态的复杂市场的影响。近年来，使用 Deep Learning 从复杂的金融信号中提取特征的方法逐渐兴起。同时，Reinforcement Learning 采用深度神经网络，来加强传统的浅投资策略（traditional shallow investment strategies）。但将技术应用在现实的金融市场中仍会面对许多挑战：

1. 收益和风险的平衡。现有的深度学习模型重在价格预测，而没有风险意识，这与基本的投资原则相悖，同时导致收益欠佳。而强化学习模型有考虑到这个问题，但如何在风险收益平衡的 RL 框架中采用最先进的 DL 方法，目前暂未有研究。
2. 对资产之间关系的建模。 市场上许多金融工具可以用来从资产之间的相互关系中获得风险意识利润，比如：BWSL策略。而现有的 RL/DL 策略很少有关注此信息。
3. 解释投资策略。即如何从 DL 和带有深层次的 RL 所支持的策略中提取可解释的规则。

2 预备知识

2.1 金融相关知识

1. Holding period：持有期。在投资一项资产中，一个持有期是 最小时间单位。我们将时间轴划分为固定长度的持有期，例如一天、一个月等。

2. Sequential investment：序列化投资。序列化投资是一个持有期的序列。对于第 t 个持有期，策略使用原始资本投资于 t 时刻的资产，并在 t+1 时刻得到利润（可正可负数）。资本加上第 t 个持有期获得的利润等于第 t+1 个持有期的原始资本。

3. Asset Price：资产价格。资产价格是一个带有时间单位的序列。 p ( i ) = { p 1 ( i ) , p 2 ( i ) , … , p t ( i ) , … } \boldsymbol{p}^{(i)}=\left\{p_{1}^{(i)}, p_{2}^{(i)}, \ldots, p_{t}^{(i)}, \ldots\right\} p(i)={p1(i)​,p2(i)​,…,pt(i)​,…}，其中 p t ( i ) p_{t}^{(i)} pt(i)​ 为在 t 时刻资产 i 的价格。

4. Long position：多头头寸。多头头寸是在 t1 时刻买入，然后在 t2 时刻卖出的交易操作。资产 i 在 t1 到 t2 之间多头头寸的利润是 u i ( p t 2 ( i ) − p t 1 ( i ) ) u_{i}\left(p_{t_{2}}^{(i)}-p_{t_{1}}^{(i)}\right) ui​(pt2​(i)​−pt1​(i)​)，也就是，投资者预料到价格会上涨，故提前买入，等价格上涨后卖出的行为。

5. Short position：空头头寸。空头头寸是在 t1 时刻卖出，然后在 t2 时刻买入的交易操作。资产 i 在 t1 到 t2 之间多头头寸的利润是 u i ( p t 1 ( i ) − p t 2 ( i ) ) u_{i}\left(p_{t_{1}}^{(i)}-p_{t_{2}}^{(i)}\right) ui​(pt1​(i)​−pt2​(i)​)，也就是，投资者因预料价格会下跌提前提出卖出价格大笔卖出或者使卖出大于买入的行为。

   一个做空的交易者从经纪人哪里借入一只股票并以 t1 的价格（高价卖）卖出，在 t2 时，交易者买回卖出的股票（低价买），然后归还给经纪人。

6. Portfolio：投资组合。投资组合定义为一个向量。每个元素是对应资产在总资产下的占比。 b = ( b ( 1 ) , … , b ( i ) , … , b ( I ) ) ⊤ \boldsymbol{b}=\left(b^{(1)}, \ldots, b^{(i)}, \ldots, b^{(I)}\right)^{\top} b=(b(1),…,b(i),…,b(I))⊤，其中 b ( i ) b^{(i)} b(i) 代表了在资产 i 上的投资比例，并且 ∑ i = 1 I b ( i ) = 1 \sum_{i=1}^{I} b^{(i)}=1 ∑i=1I​b(i)=1。

   $M$：投资组合的资金。

   

7. Zero-Investment portfolio：零投资组合。Zero-Investment portfolio 是投资组合的集合，其净资产总额为零。比如，A 买了（做多）X公司的一股股票，那么他完全受到该股票价值变动的影响。但如果，A 同时卖出（做空）同一支股票，那么任何变动的影响都将被抵消。所以，多头和空头头寸的组合就是一个零投资组合。

2.2 BWSL策略

Buy-winners-and-sell-losers 的核心就是 买入价格涨幅高的资产（winners），卖出价格涨幅低的资产（losers）。

本文使用零投资组合的方式执行 BWSL 策略，包括两种组合：买入赢家的多头组合 和 卖出输家的空头组合。

1. 首先，在 t 时刻，借入“loser”股票并卖出（做空）。我们能借到的股票 i 的数量如下。其中，bt-(i) 为股票 i 在空头组合中所占比例。
u t − ( i ) = M ~ ⋅ b t − ( i ) / p t ( i ) u_{t}^{-(i)}=\tilde{M} \cdot b_{t}^{-(i)} / p_{t}^{(i)} ut−(i)​=M~⋅bt−(i)​/pt(i)​
2. 然后，在 t 时刻，买入“winner”（做多）。我们能买入股票 i 的数量如下。
u t + ( i ) = M ~ ⋅ b t + ( i ) / p t ( i ) u_{t}^{+(i)}=\tilde{M} \cdot b_{t}^{+(i)} / p_{t}^{(i)} ut+(i)​=M~⋅bt+(i)​/pt(i)​
这里用来做多的资金 M 是之前卖空的收益，因此投资组合的净投资为0。

3. 在 t 时刻结束时，卖出多头组合。 我们能得到的金额是所有股票在 t+1 时以新价格p_t+1出售股票的收益。
M t + = ∑ i = 1 I u t + ( i ) p t + 1 ( i ) = ∑ i = 1 I M ~ ⋅ b t + ( i ) p t + 1 ( i ) p t ( i ) M_{t}^{+}=\sum_{i=1}^{I} u_{t}^{+(i)} p_{t+1}^{(i)}=\sum_{i=1}^{I} \tilde{M} \cdot b_{t}^{+(i)} \frac{p_{t+1}^{(i)}}{p_{t}^{(i)}} Mt+​=i=1∑I​ut+(i)​pt+1(i)​=i=1∑I​M~⋅bt+(i)​pt(i)​pt+1(i)​​
4. 同时，在 t 时刻结束时，买回空头组合并归还。 买回股票所需要花费如下。
M t − = ∑ i = 1 I u t − ( i ) p t + 1 ( i ) = ∑ i = 1 I M ~ ⋅ b t − ( i ) p t + 1 ( i ) p t ( i ) M_{t}^{-}=\sum_{i=1}^{I} u_{t}^{-(i)} p_{t+1}^{(i)}=\sum_{i=1}^{I} \tilde{M} \cdot b_{t}^{-(i)} \frac{p_{t+1}^{(i)}}{p_{t}^{(i)}} Mt−​=i=1∑I​ut−(i)​pt+1(i)​=i=1∑I​M~⋅bt−(i)​pt(i)​pt+1(i)​​
计算收益情况：

回报率计算：
R t = M t M ~ = ∑ i = 1 I b t + ( i ) z t ( i ) − ∑ i = 1 I ′ b t − ( i ) z t ( i ) R_{t}=\frac{M_{t}}{\tilde{M}}=\sum_{i=1}^{I} b_{t}^{+(i)} z_{t}^{(i)}-\sum_{i=1}^{I^{\prime}} b_{t}^{-(i)} z_{t}^{(i)} Rt​=M~Mt​​=i=1∑I​bt+(i)​zt(i)​−i=1∑I′​bt−(i)​zt(i)​
如果我们想要 Rt > 0，那么需要：
∑ i = 1 I b t + ( i ) z t ( i ) > ∑ i = 1 I ′ b t − ( i ) z t ( i ) \sum_{i=1}^{I} b_{t}^{+(i)} z_{t}^{(i)}>\sum_{i=1}^{I^{\prime}} b_{t}^{-(i)} z_{t}^{(i)} i=1∑I​bt+(i)​zt(i)​>i=1∑I′​bt−(i)​zt(i)​
可以看出，BWSL 策略看重的是相对价格。尽管整个股票市场的所有股票都在跌，只要有 b+ 跌的速度小于 b- 跌的速度，就能保证获利。

2.3 优化目标

为了保证同时考虑风险和收益，本文采用的是 Sharpe radtio 来评估策略的表现。单位波动率超过无风险投资汇报的平均回报。
H T = A T − Θ V T H_{T}=\frac{A_{T}-\Theta}{V_{T}} HT​=VT​AT​−Θ​
举例而言，假如国债的回报是3%，而你的投资组合预期回报是15%，你的投资组合的标准偏差是6%，那么用15%－3%,可以得出12%（代表超出无风险投资的回报），再用12%/6%=2，代表投资者风险每增长1%，换来的是2%的多余收益。

3 AlphaStock 模型框架

AlphaStack 是一个基于深层注意力网络的强化学习方法。它的本质上就是 BWSL（buying winners and selling losers） 策略。它由三部分组成。

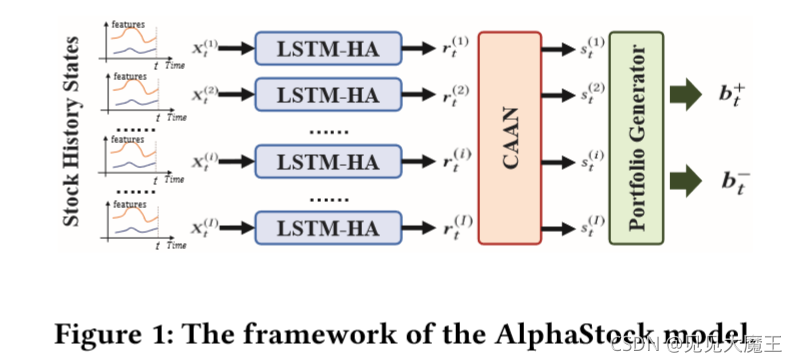
1. LSTM-HA。即带 history attention 的 LSTM 网络，用于从多个时间序列中提取资产表示。
2. Cross-Asset Attention Networks（CAAN），即跨资产注意力网络。该网络能够充分模拟资产之间的相互关系以及资产价格上涨的先验情况。
3. Portfolio generator，即投资组合生成器。根据注意力网络的输出赢家分数给出每种资产的投资比例。

使用 RL 框架来优化模型。优化目标为 return-risk-balanced objective（收益-风险的平衡），即 Sharpe Radtio。

Sharpe Radtio：计算投资组合每一单位总风险，会产生多少的超额报酬。理性的投资者将选择并持有有效的投资组合，即那些在给定的风险水平下使期望回报最大化的投资组合，或那些在给定期望回报率的水平上使风险最小化的投资组合。

进一步，为了增加 AlphaStock 的可解释性，作者提出了 seneitivity analysis method（敏感性分析方法），以解释模型如何根据输入的多角度特征来选择资产进行投资。

3.1 原始特征

模型包括两种特征：技术面 和 基本面。具体为如下七个：

首先是三个技术面：

1. Price Rising Rate（PR）：在最后一个持有期内股票价格上涨的速度。对于每个股票 i，定义为： ( p t i / p t − 1 i ) (p_t^i / p_{t-1}^i) (pti​/pt−1i​)
2. Fine-grained Volatility（VOL）：一个持有期可以被进一步划分为多个子阶段。本文设置一个月为持有期，因此一个子阶段可以是一个交易日。VOL 定义为从 t-1 到 t 的所有子阶段价格的标准差。
3. Trade Volume（TV）：从 t-1 到 t 的股票交易总量。它反映了股票的市场活动。

然后是四个基本面：

1. Market Capitalization（MC）：市值，是一种度量公司资产规模的方式，数量上等于该公司当前的 股票价格 乘以该公司 所有的普通股数量。市值通常可以用来作为收购某公司的成本评估，市值的增长通常作为一个衡量该公司经营状况的关键指标。市值也会受到非经营性因素的影响而产生变化，例如收购和回购。
2. Price-earnings Ratio（PE）：市盈率，公司市值与其年度收益的比率。
3. Book-to-market Ratio（BM）：账面市值比，公司账面价值与市场价值比率。
4. Dividend（Div）：公司在第 t-1 个持有期内，从公司收益中给股东的奖励。

3.2 股票特征提取

在 t 时刻的历史状态使用向量表示上述特征，记为 x t x_t xt​。

Look-back window（回顾窗口）：时刻 t 上的最后 K 个历史持有期，即从时刻 t-K 到 t 的时期。本文将回顾窗口表示为一个关于 x 的矩阵 $X$， X = { x 1 , … , x k , … , x K } 1 , where  x k = x ~ t − K + k X=\left\{x_{1}, \ldots, x_{k}, \ldots, x_{K}\right\}^{1}, \text { where } x_{k}=\tilde{x}_{t-K+k} X={x1​,…,xk​,…,xK​}1, where xk​=x~t−K+k​。

本文使用 LSTM 网络将矩阵 $X$ 递归编码为向量：
h k = LSTM ⁡ ( h k − 1 , x k ) , k ∈ [ 1 , K ] \boldsymbol{h}_{k}=\operatorname{LSTM}\left(\boldsymbol{h}_{k-1}, \boldsymbol{x}_{k}\right), k \in[1, K] hk​=LSTM(hk−1​,xk​),k∈[1,K]
其中， h k h_k hk​ 是 LSTM 在第 k 步编码的隐藏状态。当走到最后一步时输出 h k h_k hk​， h k h_k hk​ 用来作为这个股票的表示。它包含了 $X$ 中元素的顺序依赖性。

进一步，本文引入了 history state attention。用所有的中间隐藏状态 h k h_k hk​ 来增强 h K h_K hK​ 。按照标准的注意力机制，增强后的表示记为 $r$。
r = ∑ k = 1 K A T T ( h K , h k ) h k r=\sum_{k=1}^{K} A T T\left(h_{K}, h_{k}\right) h_{k} r=k=1∑K​ATT(hK​,hk​)hk​

ATT ⁡ ( h K , h k ) = exp ⁡ ( α k ) ∑ k ′ = 1 K exp ⁡ ( α k ′ ) α k = w ⊤ ⋅ tanh ⁡ ( W ( 1 ) h k + W ( 2 ) h K ) \begin{aligned} \operatorname{ATT}\left(\boldsymbol{h}_{K}, \boldsymbol{h}_{k}\right) &=\frac{\exp \left(\alpha_{k}\right)}{\sum_{k^{\prime}=1}^{K} \exp \left(\alpha_{k^{\prime}}\right)} \\ \alpha_{k} &=\boldsymbol{w}^{\top} \cdot \tanh \left(\boldsymbol{W}^{(1)} \boldsymbol{h}_{k}+\boldsymbol{W}^{(2)} \boldsymbol{h}_{K}\right) \end{aligned} ATT(hK​,hk​)αk​​=∑k′=1K​exp(αk′​)exp(αk​)​=w⊤⋅tanh(W(1)hk​+W(2)hK​)​

其中， w , W ( 1 ) , W ( 2 ) w,W^{(1)},W^{(2)} w,W(1),W(2) 都是需要训练的参数。

3.3 Winners 与 Losers 的选择

首先使用 The Basic CAAN Model 来对股票之间的相互关系建模。

CAAN模型采用 自注意力机制，给定股票的表示 r ( i ) r^{(i)} r(i)，我们为股票 i 计算一个查询向量 q ( i ) q^{(i)} q(i)，一个关键向量 k ( i ) k^{(i)} k(i) 和一个值向量 v ( i ) v^{(i)} v(i)。其中，下式的三个 $W$ 是需要学习的参数。
q ( i ) = W ( Q ) r ( i ) , k ( i ) = W ( K ) r ( i ) , v ( i ) = W ( V ) r ( i ) q^{(i)}=W^{(Q)} r^{(i)}, k^{(i)}=W^{(K)} r^{(i)}, v^{(i)}=W^{(V)} r^{(i)} q(i)=W(Q)r(i),k(i)=W(K)r(i),v(i)=W(V)r(i)
股票 j 与股票 i 的 相互关系 建模为：使用股票 i 的 q ( i ) q^{(i)} q(i) 来查询股票 j 的 k ( i ) k^{(i)} k(i)，即：(其中 Dk 是缩放参数)。
β i j = q ( i ) ⊤ ⋅ k ( j ) D k \beta_{i j}=\frac{\boldsymbol{q}^{(i) \top} \cdot \boldsymbol{k}^{(j)}}{\sqrt{D_{k}}} βij​=Dk​ ​q(i)⊤⋅k(j)​
然后，本文将归一化的 相互关系 β i j \beta_{ij} βij​ 作为权重，将其他股票的 v ( j ) v^{(j)} v(j) 值相加，计算得分 a。其中 SATT 为注意力函数。
a ( i ) = ∑ j = 1 I SATT ⁡ ( q ( i ) , k ( j ) ) ⋅ v ( j ) SATT ⁡ ( q ( i ) , k ( j ) ) = exp ⁡ ( β i j ) ∑ j ′ = 1 I exp ⁡ ( β i j ′ ) a^{(i)}=\sum_{j=1}^{I} \operatorname{SATT}\left(q^{(i)}, k^{(j)}\right) \cdot v^{(j)}\\ \operatorname{SATT}\left(\boldsymbol{q}^{(i)}, \boldsymbol{k}^{(j)}\right)=\frac{\exp \left(\beta_{i j}\right)}{\sum_{j^{\prime}=1}^{I} \exp \left(\beta_{i j^{\prime}}\right)} a(i)=j=1∑I​SATT(q(i),k(j))⋅v(j)SATT(q(i),k(j))=∑j′=1I​exp(βij′​)exp(βij​)​
本文使用全连接层将注意力向量 a 转化为 winner 得分：
s ( i ) = sigmoid ⁡ ( w ( s ) ⊤ ⋅ a ( i ) + e ( s ) ) s^{(i)}=\operatorname{sigmoid}\left(w^{(s) \top} \cdot a^{(i)}+e^{(s)}\right) s(i)=sigmoid(w(s)⊤⋅a(i)+e(s))

其中 w, e 两个向量分别是全连接层的 weight 和 bias，需要训练得出。

winner 得分 s t ( i ) s_{t}^{(i)} st(i)​ 说明：股票 i 在第 t 个持有期内成为 winner 的程度。一只得分较高的股票更有机会成为 winner。

进一步，作者提出可以使用 历史的价格上涨率排名的先验知识 来学习股票之间的关系，也就是上文的 β i j \beta_{ij} βij​。

本文用 c t − 1 ( i ) c_{t-1}^{(i)} ct−1(i)​ 表示股票 i 在 上一次持有期间（从 t-1 到 t） 的价格上升率的排名。然后，使用股票 在 c t − 1 ( i ) c_{t-1}^{(i)} ct−1(i)​ 坐标上的相对位置 作为股票 相互关系的先验知识。在 c t − 1 ( i ) c_{t-1}^{(i)} ct−1(i)​ 坐标轴上计算它们的 离散相对距离。

d i j = ⌊ ∣ c t − 1 ( i ) − c t − 1 ( j ) ∣ / Q ⌋ . d_{i j}=\left \lfloor {\left|c_{t-1}^{(i)}-c_{t-1}^{(j)}\right| / Q}\right \rfloor . dij​=⌊∣∣∣​ct−1(i)​−ct−1(j)​∣∣∣​/Q⌋.

其中，$Q$ 是预设的量化系数。本文使用查找矩阵 L = ( l 1 , … , l L ) L=\left(l_{1}, \ldots, l_{L}\right) L=(l1​,…,lL​) 来表示每个离散值 d i j d_{ij} dij​。以 d i j d_{ij} dij​ 为索引，对应的列向量 l d i j l_{d_{ij}} ldij​​ 相对距离 的嵌入向量 d i j d_{ij} dij​。然后，作者使用列向量 l d i j l_{d_{ij}} ldij​​ 计算先验关系系数 ψ i j \psi_{ij} ψij​。
ψ i j = sigmoid ⁡ ( w ( L ) ⊤ l d i j ) \psi_{i j}=\operatorname{sigmoid}\left(w^{(L) \top} l_{d_{i j}}\right) ψij​=sigmoid(w(L)⊤ldij​​)
其中 w 是一个可学习的参数。因此，股票 i 与股票 j 之间的关系可以按照下式计算：
β i j = ψ i j ( q ( i ) ⊤ ⋅ k ( j ) ) D \beta_{i j}=\frac{\psi_{i j}\left(\boldsymbol{q}^{(i) \top} \cdot \boldsymbol{k}^{(j)}\right)}{\sqrt{D}} βij​=D ​ψij​(q(i)⊤⋅k(j))​
计算完成之后的步骤跟 The Basic CAAN Model 后续步骤一样，计算出 winner 得分即可。

3.4 投资组合生成器

首先，作者根据 winner 得分把股票进行降序排列，得到每只股票的 i 的序号 o ( i ) o^{(i)} o(i)。设置 $G$ 为组合 b + b^{+} b+ 和 b − b^{-} b− 的预设规模。选取前 G 个用作多头，最后 G 个用作空头。

如果 o ( i ) ∈ [ 1 , G ] o^{(i)} \in[1, G] o(i)∈[1,G]，股票 i 将进入 b + ( i ) b^{+(i)} b+(i):
b + ( i ) = exp ⁡ ( s ( i ) ) ∑ o ( i ′ ) ∈ [ 1 , G ] exp ⁡ ( s ( i ′ ) ) b^{+(i)}=\frac{\exp \left(s^{(i)}\right)}{\sum_{o^{{\left(i^{\prime}\right)}} \in[1, G]}\exp \left(s^{\left(i^{\prime}\right)}\right)} b+(i)=∑o(i′)∈[1,G]​exp(s(i′))exp(s(i))​
如果 o ( i ) ∈ [ I − G , I ] o^{(i)} \in[I-G, I] o(i)∈[I−G,I]，股票 i 将进入 b − ( i ) b^{-(i)} b−(i):
b − ( i ) = exp ⁡ ( 1 − s ( i ) ) ∑ o ( i ′ ) ∈ [ I − G , I ] exp ⁡ ( 1 − s ( i ′ ) ) b^{-(i)}=\frac{\exp \left(1-s^{(i)}\right)}{\sum_{o^{{\left(i^{\prime}\right)}} \in[I-G, I]}\exp \left(1-s^{\left(i^{\prime}\right)}\right)} b−(i)=∑o(i′)∈[I−G,I]​exp(1−s(i′))exp(1−s(i))​
最后记作 b c b^c bc 维度是 I，前 G 维和 b + b^+ b+ 相同，后G维和 b − b^- b− 相同，其余维度是0.

3.5 使用RL进行优化

作者通过将 AlphaStock 的策略转化为具有离散 action 的RL过程来优化模型参数。因此，具有 $T$ 个持有期的投资序列被模型化为一个 trajectory π = s t a t e 1 , a c t i o n 1 , r e w a r d 1 , . . . , s t a t e t , a c t i o n t , r e w a r d t , . . . s t a t e T , a c t i o n T , r e w a r d T \pi = {state_1, action_1,reward_1,...,state_t,action_t,reward_t,...state_T,action_T,reward_T} π=state1​,action1​,reward1​,...,statet​,actiont​,rewardt​,...stateT​,actionT​,rewardT​。其中 s t a t e t state_t statet​ 是在第 t 时刻所观察到的历史市场状态，表示为 X t = ( X t ( i ) ) X_t=(X_t^{(i)}) Xt​=(Xt(i)​)； a c t i o n t action_t actiont​ 是一个 $I$ 维的二维向量，当 a c t i o n t = 1 action_t = 1 actiont​=1 时，表示 agent 在 t 时刻选择投资股票 i。根据不同的历史状态，agent 对是否投资股票 i 这个行为具有一个概率 Pr ⁡ ( a c t i o n t ( i ) = 1 ) \Pr(action_t^{(i)}=1) Pr(actiont(i)​=1)。
Pr ⁡ ( action  t ( i ) = 1 ∣ X t n , θ ) = 1 2 G ( i ) ( X t n , θ ) = 1 2 b t c ( i ) \operatorname{Pr}\left(\text { action }_{t}^{(i)}=1 \mid X_{t}^{n}, \theta\right)=\frac{1}{2} \mathcal{G}^{(i)}\left(X_{t}^{n}, \theta\right)=\frac{1}{2} b_{t}^{c(i)} Pr( action t(i)​=1∣Xtn​,θ)=21​G(i)(Xtn​,θ)=21​btc(i)​

其中， G ( i ) ( X t n , θ ) \mathcal{G}^{(i)}(X_{t}^{n}, \theta) G(i)(Xtn​,θ) 是 AlphaStock 的一部分，用于生成 b t c ( i ) b_t^{c(i)} btc(i)​；$\theta$ 代表模型的参数。使用 H π H_\pi Hπ​ 表示一个 trajectory $\pi$ 的夏普比率，

那么 r e w a r d t reward_t rewardt​ 就是 a c t i o n t action_t actiont​ 对 H π H_\pi Hπ​ 的贡献大小，同时有 ∑ i = 1 I r e w a r d t = H π \sum^I_{i=1}reward_t=H_\pi ∑i=1I​rewardt​=Hπ​。

对于所有可能的 trajectory $\pi$，平均 reward 为：
J ( θ ) = ∫ π H π Pr ⁡ ( π ∣ θ ) d π J(\theta)=\int_{\pi} H_{\pi} \operatorname{Pr}(\pi \mid \theta) \mathrm{d} \pi J(θ)=∫π​Hπ​Pr(π∣θ)dπ
其中，$\mathrm{Pr}(\pi \mid \theta )$ 为根据 $\theta$ 生成 $\pi$ 的概率。于是 RL 模型的最优化转化为找到一组最优的参数 θ ∗ = argmax ⁡ θ J ( θ ) \theta^* = \operatorname{argmax}_\theta J(\theta) θ∗=argmaxθ​J(θ)。使用梯度上升迭代优化。

对 $J(\theta )$ 进行求导：

∇ J ( θ ) = ∫ π H π Pr ⁡ ( π ∣ θ ) ∇ log ⁡ Pr ⁡ ( π ∣ θ ) d π ≈ 1 N ∑ n = 1 N ( H π n ∑ t = 1 T n ∑ i = 1 I ∇ θ log ⁡ Pr ⁡ ( action  t ( i ) = 1 ∣ X t ( n ) , θ ) ) \begin{aligned} \nabla J(\theta) &=\int_{\pi} H_{\pi} \operatorname{Pr}(\pi \mid \theta) \nabla \log \operatorname{Pr}(\pi \mid \theta) \mathrm{d} \pi \\ & \approx \frac{1}{N} \sum_{n=1}^{N}\left(H_{\pi_{n}} \sum_{t=1}^{T_{n}} \sum_{i=1}^{I} \nabla_{\theta} \log \operatorname{Pr}\left(\text { action }_{t}^{(i)}=1 \mid X_{t}^{(n)}, \theta\right)\right) \end{aligned} ∇J(θ)​=∫π​Hπ​Pr(π∣θ)∇logPr(π∣θ)dπ≈N1​n=1∑N​(Hπn​​t=1∑Tn​​i=1∑I​∇θ​logPr( action t(i)​=1∣Xt(n)​,θ))​

∇ θ log ⁡ Pr ⁡ ( action  t ( i ) = 1 ∣ X t ( n ) , θ ) = ∇ θ log ⁡ G ( i ) ( X t n , θ ) \nabla_{\theta} \log \operatorname{Pr}\left(\text { action }_{t}^{(i)}=1 \mid \mathcal{X}_{t}^{(n)}, \theta\right)=\nabla_{\theta} \log \mathcal{G}^{(i)}\left(\mathcal{X}_{t}^{n}, \theta\right) ∇θ​logPr( action t(i)​=1∣Xt(n)​,θ)=∇θ​logG(i)(Xtn​,θ)

为了保证模型至少能够打败市场（最简单的买入持有策略），作者引入了一个阈值 H 0 H_0 H0​，该值为整个市场的夏普率。
∇ J ( θ ) = 1 N ∑ n = 1 N ( ( H π n − H 0 ) ∑ t = 1 T n ∑ i = 1 I ∇ θ log ⁡ G ( i ) ( X t n , θ ) ) \nabla J(\theta)=\frac{1}{N} \sum_{n=1}^{N}\left(\left(H_{\pi_{n}}-H_{0}\right) \sum_{t=1}^{T_{n}} \sum_{i=1}^{I} \nabla_{\theta} \log \mathcal{G}^{(i)}\left(\mathcal{X}_{t}^{n}, \theta\right)\right) ∇J(θ)=N1​n=1∑N​((Hπn​​−H0​)t=1∑Tn​​i=1∑I​∇θ​logG(i)(Xtn​,θ))
通过这样，梯度上升只会奖励那些超过市场表现的参数。

4 模型解释

作者希望研究分析：AlphaStock 会选择什么类型的股票？

为此，作者提出引入了 灵敏度分析方法（sensitivity analysis method）。作者使用 $s=\mathcal{F}(\mathbf{X})$ 来表示从股票的历史特征 $X$ 到它的赢家得分 $s$ 的映射；使用 x q x_q xq​ 表示 $X$ 中的一个元素（也就是其中一个特征）。当给定一个股票的历史状态 $X$，特征 x q x_q xq​ 对 $s$ 的影响（灵敏度）为：
δ x q ( X ) = lim ⁡ Δ x q → 0 F ( X ) − F ( x q + Δ x q , X ¬ x q ) x q − ( x q + Δ x q ) = ∂ F ( X ) ∂ x q , \delta_{x_{q}}(X)=\lim _{\Delta x_{q} \rightarrow 0} \frac{\mathcal{F}(X)-\mathcal{F}\left(x_{q}+\Delta x_{q}, X_{\neg x_{q}}\right)}{x_{q}-\left(x_{q}+\Delta x_{q}\right)}=\frac{\partial \mathcal{F}(X)}{\partial x_{q}}, δxq​​(X)=Δxq​→0lim​xq​−(xq​+Δxq​)F(X)−F(xq​+Δxq​,X¬xq​​)​=∂xq​∂F(X)​,
下一步，对于市场中所有可能的股票历史状态，计算特征 x q x_q xq​ 对得分的平均影响（灵敏度）：
δ ˉ x q = ∫ D X Pr ⁡ ( X ) δ x q ( X ) d σ \bar{\delta}_{x_{q}}=\int_{D_{X}} \operatorname{Pr}(X) \delta_{x_{q}}(X) \mathrm{d}_{\sigma} δˉxq​​=∫DX​​Pr(X)δxq​​(X)dσ​
其中，$\mathrm{Pr}(X)$ 是 $X$ 的概率密度函数。给定 I 只股票在 N 个持有期内的历史状态，根据大数定律有：
δ ˉ x q = 1 I × N ∑ n = 1 N ∑ i = 1 I δ x q ( X n ( i ) ∣ X n ( ¬ i ) ) \bar{\delta}_{x_{q}}=\frac{1}{I \times N} \sum_{n=1}^{N} \sum_{i=1}^{I} \delta_{x_{q}}\left(X_{n}^{(i)} \mid X_{n}^{(\neg i)}\right) δˉxq​​=I×N1​n=1∑N​i=1∑I​δxq​​(Xn(i)​∣Xn(¬i)​)
其中， X n ( i ) X_{n}^{(i)} Xn(i)​ 为第 i 只股票在第 n 个持有期内的历史状态，后者为其他股票的历史状态。

于是，我们使用 δ ˉ x q \bar{\delta}_{x_{q}} δˉxq​​ 来衡量不同特征对股票得分的影响。当值为整数时，说明随着该特征的值不断增大，模型更加认为它是winner，反之亦然。

5 实验与关键结果

5.1 对比方法

作者使用了4种对比方法：

1. Market，简单的买入并持有方法。
2. Cross Sectional Momentum（CSM）和 Time Series Momentum（TSM），两种经典的动量方法。
3. Robust Median Reversion（RMR），逆转策略。
4. Fuzzy Deep Direct Reinforcement（FDDR），基于RL的BWSL策略。

以及自身对比方法：

5. AlphaStock-NC：去除 CAAN。
6. AlphaStock-NP：去除价格上涨排名的先验知识。

5.2 评价指标

5.3 实验结果

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！