信息与不确定性

最近学习了吴军的《信息论40讲》，深有感触，有感而发！

本博文想要给你传递（或者说洗脑）两个主要观点：

“信息是可以量化的，用事件的不确定性表示”，

“增加相关信息，会减小其不确定性”。

咱们先搞清楚以下五个概念，他们是层层递进的。

1. 信息量
2. 信息熵
3. 交叉熵
4. 相对熵
5. 互信息

一、信息量

咱们一起来玩一玩Yes or No的游戏。随便你问什么都可以，但我的答案只有YES或者NO。

我随便抛出一枚硬币，并且把硬币双手合着，你猜朝上的那一面是什么？

如果你问我朝上的，是不是“中国人民银行”，我告诉你NO，那你就知道是什么了。也就是说，你只要获取1bit的信息就可以知道结果了，事件就是确定的了。

如果我摇色子，你想要知道朝上的数字，那你只问我一个问题就很难得到结果了，因为此时的不确定性增加了，1bit的信息hold不住了。

One more question，

这个问题很有意思，让你感受到多读书还是有用的，至少不需要弄死那么多的小白鼠。

解答如下：

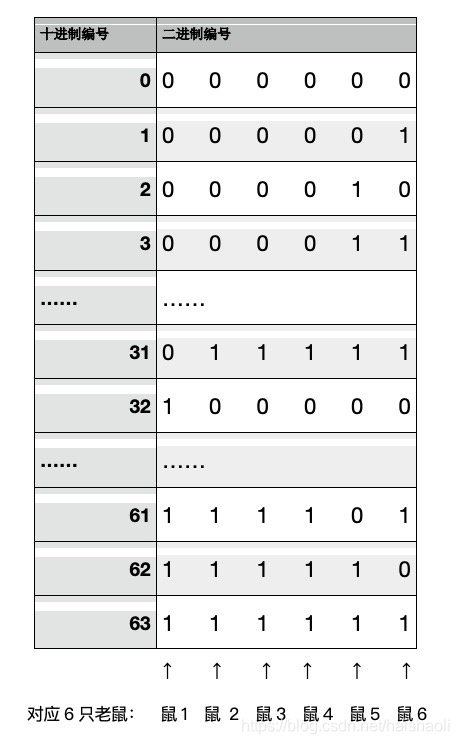
1、我们将这些药从0～63按照二进制编号，获得64个六位数的二进制编号，也就是从000000（六个零）到111111（六个一），每个二进制编号的最左边是第一位，最右边是第六位。

2、然后选六只老鼠从左到右排开，和二进制的六位，从左到右地依次对应。文稿里的二进制编号，你可以试着一位一位竖着看，下面每只老鼠负责一位。

3、从左边数第一个老鼠吃对应的二进制是1的药，0就不吃。那么老鼠1依次吃第32，33，34，……，63号药。第二只吃16，17，……，31，48，49，……，63号药，等等。最后一只老鼠吃1，3，5，……，63号药。你可能注意到了，6只老鼠都吃了63号，那是因为63对应的二进制编号是6个1，所以6只都要吃。

4、吃完药之后三天，某些老鼠可能死了，我们假定第1，2，6这三只老鼠死了，剩下的活着。这说明什么呢？说明编号110001号药有问题，也就是在第1，第2，第6位上分别是3个1，因为这三只老鼠都吃了它，而3，4，5这三只没死的老鼠没有吃它（对应的位置为0）。而110001对应十进制的49，也就是说第49瓶药是毒药。

实际上解决这个问题只要六只小老鼠就可以了，这是一个64选1的题目，那么需要的信息量就是log64，也就是6比特。

例子讲完了，来一些枯燥的吧。

二、信息熵

三、交叉熵

四、相对熵

五、互信息

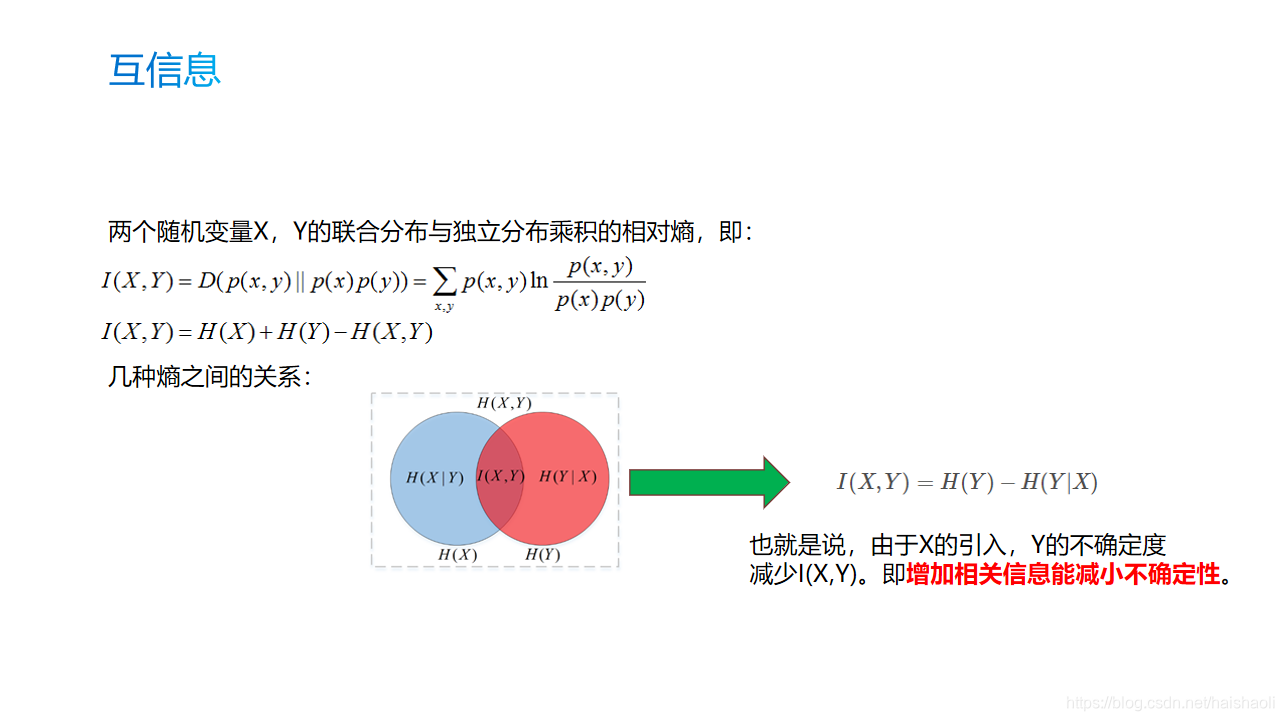
图中的I(X,Y)是指不确定性减少的量。如果X和Y是独立分布的，没有交叉（相关性），则I(X,Y) = 0。

咱们通过引入相关信息X，成功的把Y的不确定性H(Y)减少为H(Y|X)。

因此，增加相关信息能减小不确定性！

再举一个枯燥的例子：

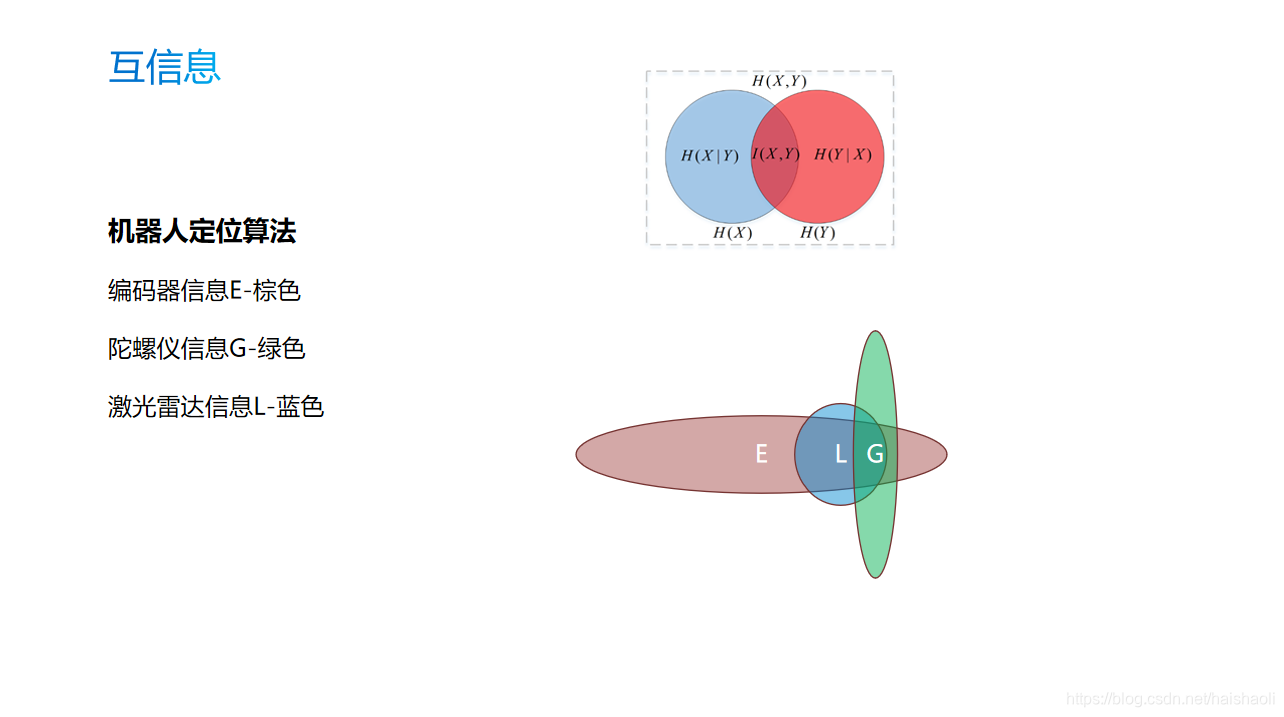
把机器人看做一个质点，机图中的E/L/G表示不同的传感器对机器人定位位置的一个估计分布。

通过多个相关信息的关联后，我们可以发现，机器人位置的不确定性明显降低了，也就是说预估更加准确了。不确定性见下图中的黄色线段部分 。

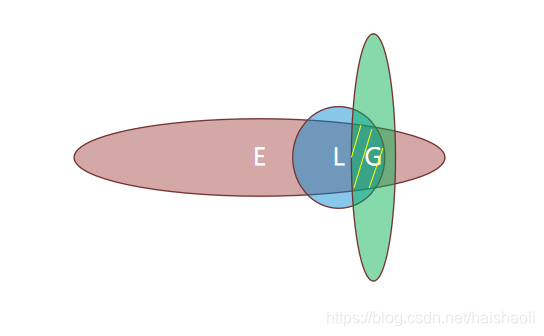
六、参考资料：

1、《信息论40讲》 吴军

2、https://blog.csdn.net/BigData_Mining/article/details/81279612

3、https://www.cnblogs.com/llhthinker/p/7287029.html

4、https://blog.csdn.net/lk7688535/article/details/52529610

5、https://www.cnblogs.com/hgl0417/p/6693656.html

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！