660-概率论-数一

660概率论总结，需要记得的部分，有些不容易忘的就没写，不是说不重要

1.理解记忆

泊松分布：

常用相关公式如下：

• 期望公式： ∑ k = 0 ∞ λ k k ! e − λ = λ \sum_{k=0}^{\infty}\frac{\lambda^k}{k!}e^{-\lambda}=\lambda ∑k=0∞​k!λk​e−λ=λ

指数分布：

常用相关公式如下：

• P { x > t + s ∣ x > s } = P { x > t } = e − λ t P\{x>t+s|x>s\}=P\{x>t\}=e^{-\lambda t} P{x>t+s∣x>s}=P{x>t}=e−λt,s,t>0

二维正态分布：

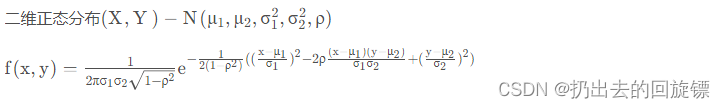
切比雪夫不等式：
要求两两不相关，存在常数c，使D(xi)小于等于c

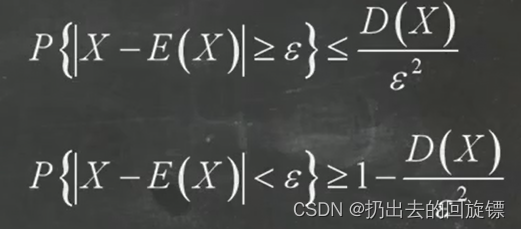
辛钦大数定律：
独立同分布并且数学期望存在

矩估计和最大似然估计求解：

常用公式：

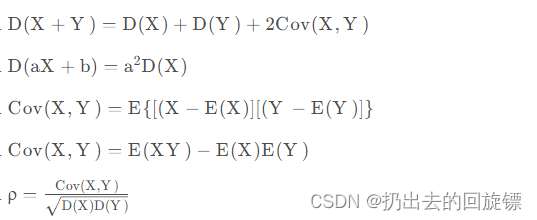
$Cov(aX+b,cY+d)=acCov(X,Y)$
$Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)$

样本估计：

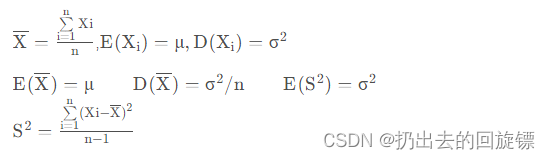
检验假设：
第 I 类错误(弃真错误)：原假设为真时拒绝原假设；
第 II 类错误(取伪错误)：原假设为假时未拒绝原假设

P{拒绝∣H0为真}=α
P{接受∣H0非真}=β
α越大，β越小，反之α越小β越大。当样本容量n增大时，α和β可以同时减小

置信区间：

其他结论：

• 必然事件发生的概率为1，但概率为1的事件不一定为必然事件;同理,不可能事件发生的概率为0，但概率为0的事件不一定为不可能事件
• A,B独立，则 B ‾ 和 A ‾ \overline{B}和\overline{A} B和A也独立。若有A、B、C两两独立，则A-B和C独立可推导ABC相互独立

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！