【数学】关于四元数的顺序无关的旋转混合的代码实现

四元数基础 + 个人理解

四元数的表达方式 Q=[x y z w]，其中x y z为矢量，是四元数的虚部，w为标量，是四算数的实部。
另外，在计算公式中，四元数的表达方式为w + v，其中w为标量，是四元数的实部，v为三维矢量。

定义：$$q=a+u=a+bi+cj+dk$$ $$p=t+v=t+xi+yj+zk$$
注：u和v为矢量

• 加法：p + q
  $$p+q=a+t+u+v=(a+t)+(b+x)i+(c+y)j+(d+z)k$$
• 乘法：qp
  $$qp=at-u・v+av+tu+u\times v$$
  $$qp=(at-bx-cy-dz)+(bt+ax+dy-cz)i+(ct+ay+bz-dx)j+(dt+za+cx-by)k$$
• 点积：p・q
  $$p・q=at+u・v=at+bx+cy+dz$$
• 共轭
  $$q\ast =a+(-u)=a-bi-cj-dk$$
• 外积：Outer(p,q)
  $$Outer(p,q)=(p\ast q-q\ast p)/2$$
  $$Outer(p,q)=at-u・v+av+tu$$
  $$Outer(p,q)=(tb-ax+cz-dy)i+(tc-ay+dx-bz)j+(td-az+by-xc)k$$
• 偶积：Even(p,q)
  $$Even(p,q)=(qp+pq)/2$$
  $$Even(p,q)=at-u・v+av+tu$$
  $$Even(p,q)=(at-bx-cy-dz)+(ax+tb)i+(ay+tc)j+(az+td)k$$
• 叉积：p×q
  $$p\times q=(pq-qp)/2$$
  $$p\times q=u\times v$$
  $$p\times q=(cz-dy)i+(dx-bz)j+(by-xc)k$$
• 逆： p − 1 p^{-1} p−1
  p − 1 = p ∗ / ( p ・ p ) p^{-1}=p*/(p・p) p−1=p∗/(p・p)
• 标量部：Scalar§
  $$1・p=(p+p\ast )/2=t$$
• 矢量部分：Vector§
  $$Outer(1,p)=(p-p\ast )/2=u=bi+cj+dk$$
• 模：|p|
  ∣ p ∣ = p ・ p = p ∗ p = a 2 + b 2 + c 2 + d 2 |p|=\sqrt{p・p}=\sqrt{p*p}=\sqrt{a^{2}+b^{2}+c^{2}+d^{2}} ∣p∣=p・p ​=p∗p ​=a2+b2+c2+d2 ​
• 符号数：sgn§
  $$sgn(p)=p/|p|$$
• 辐角：arg§
  $$arg(p)=arccos(Scalar(p)/|p|)$$
• 幂和对数
  因为四元数有除法，所以幂和对数都可以定义
• 自然幂：
  $$exp(p)=exp(a)(cos(|u|)+sgn(u)sin(u))$$
• 自然对数：$$ln(p)=ln(|p|)+sgn(u)arg(p)$$
• 幂： p q = e q ∗ l n ( p ) p^{q}=e^{q*ln(p)} pq=eq∗ln(p)
• 三角函数：
• 正弦：$$sin(p)=sin(a)cosh(|u|)+cos(a)sgn(u)sinh(|u|)$$
• 余弦：$$cos(p)=cos(a)cosh(|u|)-sin(a)sgn(u)sinh(|u|)$$
• 正切：$$tan(p)=sin(p)/cos(p)$$
• 双曲函数：
• 双曲正弦：$$sinh(p)=sinh(a)cos(|u|)+cosh(a)sgn(|u|)sin(|u|)$$
• 双曲余弦：$$cosh(p)=cosh(a)cos(|u|)+sinh(a)sgn(|u|)sin(|u|)$$
• 双曲正切：$$tanh(p)=sinh(p)/cosh(p)$$
• 反双曲函数：
• 反双曲正弦： a r c s i n h ( p ) = l n ( p + p 2 + 1 ) arcsinh(p)=ln(p+\sqrt{p^2+1}) arcsinh(p)=ln(p+p2+1 ​)
• 反双曲余弦： a r c c o s h ( p ) = l n ( p + p 2 − 1 ) arccosh(p)=ln(p+\sqrt{p^2-1}) arccosh(p)=ln(p+p2−1 ​)
• 反双曲正切：$$arctanh(p)=(ln(1+q)-ln(1-q))/2$$
• 反三角函数：
• 反正弦函数：$$arcsin(p)=-sgn(u)arcsinh(p\ast sgn(u))$$
• 反余弦函数：$$arccos(p)=-sgn(u)arccosh(p)$$
• 反正切函数：$$arctan(p)=-sgn(u)arctanh(p\ast sgn(u))$$

1. 问题
   我所在的项目之中，需要通过各种各样的传感器来获取相应的【资源】，比如使用相机获取到的照片，使用LiDAR获取到的点阵。在此，不仅需要获取【资源】本身，还需要获取到有关该【资源】的【元数据】。比如【资源】的获取时间，获取时传感器所在的位置，以及传感器获取【资源】时的姿势数据等等。我们基于团队所开发的框架之下，定义了一个统一的坐标系。但是并不排除作为一名使用框架的开发者，会希望在自己定义的坐标系下进行数据获取与计算等。所以就涉及到了坐标系与坐标系之间的转换，其中缩放与位移在坐标系之间呈线性关系，是需要简单的相加或相乘。

   但是一旦涉及到旋转，问题就变得复杂的多。因为旋转操作所构成的空间是非线性的，无法对旋转操作进行直接的线性叠加。表示旋转的四元数也不能进行直接简单的线性叠加，而且旋转的操作具有不可交换性，顺序不同也会使得结果不同。
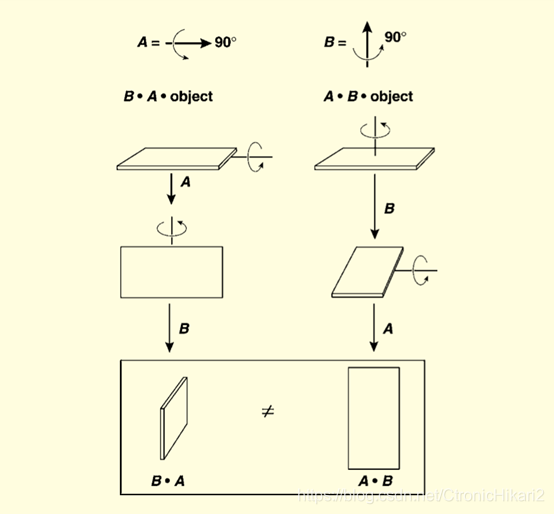
   对于在某一个坐标系的基础上，通过旋转来定义另一个坐标系，则需要定义这个旋转。而方法无非有三种，欧拉角，旋转矩阵和四元数。很明显，欧拉角是最直观的一个，但反而是最复杂的一个。定义一个三维的旋转，不仅需要定义三个轴的旋转顺序与旋转大小，而且还要小心避免出现万向节死锁的情况，可以作为API输入参数设计，以降低应用程序开发者的使用门槛，但是在内部计算时就显得不是很合适。其次是旋转矩阵，旋转矩阵因为元素太多不适合作为参数输入，并且再计算式要尤为注意矩阵的左乘右乘与相乘的顺序。所以，四元数相较于欧拉角和矩阵就成了一个折中的方案，首先需要元素少，只有四个元素，易作为参数的输入。另外四元数在数学上定义了计算方法，可以进行比较复杂的处理。缺点则是四元数相对抽象，使用门槛也高，而且计算较为复杂。

2. 理论
   假设有两个旋转q1与q2，我们把q1与q2分成两份，并且依次乘每个四元数的一半。则有，
   q1在前： q 1 1 / 2 ∗ q 2 1 / 2 ∗ q 1 1 / 2 ∗ q 2 1 / 2 q1^{1/2} * q2^{1/2} * q1^{1/2} * q2^{1/2} q11/2∗q21/2∗q11/2∗q21/2
   q2在前： q 2 1 / 2 ∗ q 1 1 / 2 ∗ q 1 1 / 2 ∗ q 1 1 / 2 q2^{1/2} * q1^{1/2} * q1^{1/2} * q1^{1/2} q21/2∗q11/2∗q11/2∗q11/2
   这使得在中间会出现一些相同的部分。假如，利用极限的思想，把q1和q2切成n份，每次只乘q1和q2的1/n一共乘n次，
   可得： ( q 1 1 / n ∗ q 2 1 / n ) n (q1^{1/n}*q2^{1/n})^{n} (q11/n∗q21/n)n
   这样，当n趋近无穷大时，中间相同的部分会越来越多，而两端剩下的不同的部分对结果的影响会越来越小。当结果为无穷时获得到趋于稳定的结果： lim ⁡ n → ∞ ( q 1 1 / n ∗ q 2 1 / n ) n \lim\limits_{n\to\infty}(q1^{1/n}*q2^{1/n})^{n} n→∞lim​(q11/n∗q21/n)n = lim ⁡ n → ∞ ( q 2 1 / n ∗ q 1 1 / n ) n \lim\limits_{n\to\infty}(q2^{1/n}*q1^{1/n})^{n} n→∞lim​(q21/n∗q11/n)n
   
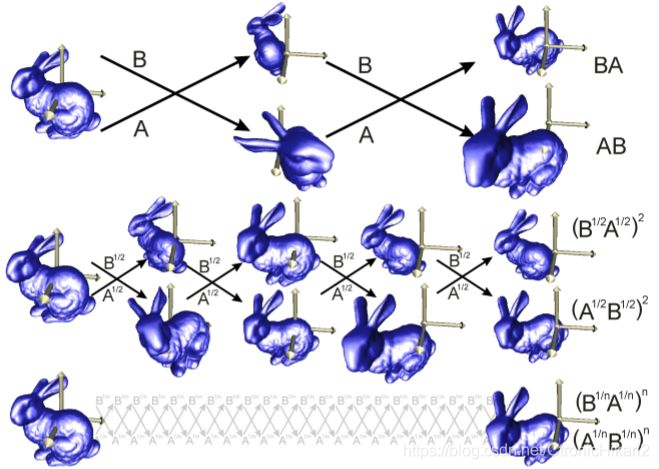
   美中不足的是极限在代码中没法使用。但是可以使用Lie product formula公式将极限问题转换为e的幂。
   e A + B = lim ⁡ n → ∞ ( e A / n ∗ e B / n ) n e^{A+B} = \lim\limits_{n\to\infty}(e^{A/n}*e^{B/n})^{n} eA+B=n→∞lim​(eA/n∗eB/n)n
   此时，令$A=lnq1$，$B=lnq2$，则有 e l n q 1 + l n q 2 = lim ⁡ n → ∞ ( e l n q 1 / n ∗ e l n q 2 / n ) n e^{lnq1+lnq2}=\lim\limits_{n\to\infty}(e^{lnq1/n}*e^{lnq2/n})^{n} elnq1+lnq2=n→∞lim​(elnq1/n∗elnq2/n)n
   可以看到，极限的运算等价于，先把四元数取对数，然后相加，最后把相加的结果进行指数运算。就得到了一个计算量是常数的计算极限的方法。
   并且，由于加法是可交换的，理论上可以在上述的极限式子中直接在塞进去更多的四元数，外可附带上权重，得到一个与顺序无关的最终旋转混合方案： q f = e ∑ i l n q i w i = e ∑ i W i ∗ l n q i q_f=e^{\sum_ilnq_i^{w_i}}=e^{\sum_iW_i*lnq_i} qf​=e∑i​lnqiwi​​=e∑i​Wi​∗lnqi​
   既Quaternion Blend(ArrayView quaternions, ArrayView weights);

3. c++代码实现

• 这里利用Eigen库实现了两个四元数的顺序无关混合。可参考该代码进行自行开发多四元数混合方案。
• 计算两个四元数的混合，既计算公式 e l n q 1 + l n q 2 e^{lnq_1+lnq_2} elnq1​+lnq2​
• 已知，p，q为四元数，则ln§，ln(q)为四元数，ln§+ln(q)为四元数，exp§也为四元数
• 必要公式1：$$ln(p)=ln(|p|)+sgn(u)arg(p)$$ $$=ln(|p|)+u/|u|\ast arccos(Scalar(p)/|p|)$$ $$=ln(|p|)+u/|u|\ast arccos(w/|p|)$$
• 必要公式2： l n ( p 1 ) + l n ( p 2 ) = l n ( ∣ p 1 ∣ ) + l n ( ∣ p 2 ∣ ) + u 1 / ∣ u 1 ∣ ∗ a r c c o s ( w 1 / ∣ p 1 ∣ ) + u 2 / ∣ u 2 ∣ + a r c c o s ( w 2 / ∣ p 2 ∣ ) ln(p_1)+ln(p_2)=ln(|p_1|)+ln(|p_2|)+u_1/|u_1|*arccos(w_1/|p_1|)+u_2/|u_2|+arccos(w_2/|p_2|) ln(p1​)+ln(p2​)=ln(∣p1​∣)+ln(∣p2​∣)+u1​/∣u1​∣∗arccos(w1​/∣p1​∣)+u2​/∣u2​∣+arccos(w2​/∣p2​∣)
• 必要公式3：$$exp(p)=exp(w)(cos(|u|)+sgn(u)sin(|u|))$$ $$=exp(w)\ast (cos(|u|)+u/|u|+sin(|u|))$$ $$=exp(w)+cos(|u|)+exp(w)\ast u/|u|\ast sin(|u|)$$

    Eigen::Quaterniond Blend2Rotations(Eigen::Quaterniond quaternion1, Eigen::Quaterniond quaternion2);//混合函数Eigen::Quaterniond lnQuaternion(Eigen::Quaterniond quaternion);//求四元数的自然对数Eigen::Quaterniond addQuaternion(Eigen::Quaterniond quaternion1, Eigen::Quaterniond quaternion2);//两四元数加和Eigen::Quaterniond expQuaternion(Eigen::Quaterniond quaternion);//求四元数的自然幂

Eigen::Quaterniond EncodeTool::Blend2Rotations(Eigen::Quaterniond quaternion1, Eigen::Quaterniond quaternion2)
{Eigen::Quaterniond logQ1 = lnQuaternion(quaternion1);Eigen::Quaterniond logQ2 = lnQuaternion(quaternion2);Eigen::Quaterniond add = addQuaternion(logQ1,logQ2);Eigen::Quaterniond blend = expQuaternion(add);return blend;
}Eigen::Quaterniond EncodeTool::lnQuaternion(Eigen::Quaterniond quaternion)
{//ln(p) = ln(|p|) + Sgn(u)*arg(p)  u:vectordouble modulusOfP = sqrt(quaternion.x()*quaternion.x() + quaternion.y()*quaternion.y() + quaternion.z()*quaternion.z() + quaternion.w()*quaternion.w());double w = log(modulusOfP); //ln(|p|)double modulusOfU = sqrt(quaternion.x()*quaternion.x() + quaternion.y()*quaternion.y() + quaternion.z()*quaternion.z());double SgnUx = quaternion.x()/modulusOfU;  //Sgn(u)double SgnUy = quaternion.y()/modulusOfU;double SgnUz = quaternion.z()/modulusOfU;double argP = acos(quaternion.w()/modulusOfP);  //arg(p)Eigen::Quaterniond lnQ(argP*SgnUx, argP*SgnUy, argP*SgnUz, w);return lnQ;
}Eigen::Quaterniond EncodeTool::addQuaternion(Eigen::Quaterniond quaternion1, Eigen::Quaterniond quaternion2)
{double x = quaternion1.x() + quaternion2.x();double y = quaternion1.y() + quaternion2.y();double z = quaternion1.z() + quaternion2.z();double w = quaternion1.w() + quaternion2.w();Eigen::Quaterniond addQ(x,y,z,w);return addQ;
}Eigen::Quaterniond EncodeTool::expQuaternion(Eigen::Quaterniond quaternion)
{//exp(p) = exp(w) + (cos(|u|)+Sgn(u)sin(|u|))double expW = exp(quaternion.w());double modulusU = sqrt(quaternion.x()*quaternion.x() + quaternion.y()*quaternion.y() + quaternion.z()*quaternion.z());double cosU = cos(modulusU);double sinU = sin(modulusU);double w = expW * cosU;double x = quaternion.x()/modulusU*expW*sinU;double y = quaternion.y()/modulusU*expW*sinU;double z = quaternion.z()/modulusU*expW*sinU;Eigen::Quaterniond expQ(x,y,z,w);return expQ;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！