【DP】模型:旅行商简化版
题型概述
给出一个图,需要从起点 A A A出发,走到终点 B B B。再从终点 B B B出发,走到起点 A A A。(两次路径经过的点不能重复)求路径最小值。
模型构建
状态设计
从某一个点出发,设 d p ( i , j ) dp(i,j) dp(i,j)表示从 i i i走到起点 A A A,再从起点 A A A出发走到 j j j所花费的最小值。
状态转移
我们用 d p ( i , j ) dp(i,j) dp(i,j)来更新下一个点 m a x ( i , j ) + 1 max(i,j)+1 max(i,j)+1;
不难得出
d p [ i ] [ k ] = m i n ( d p [ i ] [ k ] , d p [ i ] [ j ] + d i s ( j , k ) ) ; dp[i][k]=min(dp[i][k],dp[i][j]+dis(j,k)); dp[i][k]=min(dp[i][k],dp[i][j]+dis(j,k));
d p [ k ] [ j ] = m i n ( d p [ k ] [ j ] , d p [ i ] [ j ] + d i s ( i , k ) ) ; dp[k][j]=min(dp[k][j],dp[i][j]+dis(i,k)); dp[k][j]=min(dp[k][j],dp[i][j]+dis(i,k));
其中, d i s ( i , k ) dis(i,k) dis(i,k)为点 i i i到点 k k k的欧几里得距离。
理解如下:
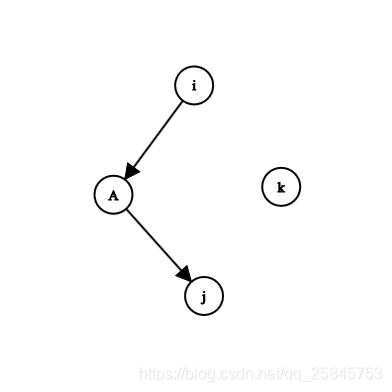
当 k k k和 i i i组合时,有: d p [ k ] [ j ] = m i n ( d p [ k ] [ j ] , d p [ i ] [ j ] + d i s ( i , k ) ) ; dp[k][j]=min(dp[k][j],dp[i][j]+dis(i,k)); dp[k][j]=min(dp[k][j],dp[i][j]+dis(i,k));
当 k k k和 j j j组合时,有: d p [ i ] [ k ] = m i n ( d p [ i ] [ k ] , d p [ i ] [ j ] + d i s ( j , k ) ) ; dp[i][k]=min(dp[i][k],dp[i][j]+dis(j,k)); dp[i][k]=min(dp[i][k],dp[i][j]+dis(j,k));
边界条件
当 i i i到终点 B B B时,直接有: d p [ B ] [ B ] = m i n ( d p [ B ] [ B ] , d p [ B ] [ j ] + d i s ( j , B ) ) ; dp[B][B]=min(dp[B][B],dp[B][j]+dis(j,B)); dp[B][B]=min(dp[B][B],dp[B][j]+dis(j,B));
当 j j j到终点 B B B时,直接有: d p [ B ] [ B ] = m i n ( d p [ B ] [ B ] , d p [ i ] [ n ] + d i s ( i , B ) ) ; dp[B][B]=min(dp[B][B],dp[i][n]+dis(i,B)); dp[B][B]=min(dp[B][B],dp[i][n]+dis(i,B));
我们令 d p ( i , j ) = i n f dp(i,j)=inf dp(i,j)=inf, d p ( 1 , 1 ) = 0 dp(1,1)=0 dp(1,1)=0
典例变形
T1:P1523 旅行商简化版
最基本的模板,直接上代码
#include T2:最短路径(MZOJ上将会出现)
 这道题在T1基础上加了第三个问。
这道题在T1基础上加了第三个问。
如何做到第一条路径必须经过 b 1 b1 b1而第二条路径必须经过 b 2 b2 b2?
我们不妨换个思路
第一条路径必须经过 b 1 b1 b1等价于第二条路径不能经过 b 1 b1 b1
同理
第二条路径必须经过 b 2 b2 b2等价于第一条路径不能经过 b 2 b2 b2
所以我们在T1的基础上把代码稍稍修改一下:
i f ( k ! = b 1 ) d p [ i ] [ k ] = m i n ( d p [ i ] [ k ] , d p [ i ] [ j ] + d i s ( j , k ) ) ; if(k!=b1) dp[i][k]=min(dp[i][k],dp[i][j]+dis(j,k)); if(k!=b1)dp[i][k]=min(dp[i][k],dp[i][j]+dis(j,k));
i f ( k ! = b 2 ) d p [ k ] [ j ] = m i n ( d p [ k ] [ j ] , d p [ i ] [ j ] + d i s ( i , k ) ) ; if(k!=b2)dp[k][j]=min(dp[k][j],dp[i][j]+dis(i,k)); if(k!=b2)dp[k][j]=min(dp[k][j],dp[i][j]+dis(i,k));
所以问题就迎刃而解啦:
#include T3:P1006 传纸条
DFS爆搜
#include 少时诵诗书,吾问无为谓。
屦及剑及加,单打独斗大。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!