机器学习技术栈

机器学习小结

• • 前言
  • 决策树
  • • • ID3 - 最大信息增益
      • C4.5 - 最大信息增益比
      • • 信息增益比
        • 处理连续数据
        • 缺失值处理
        • 决策树剪枝
        • • 预剪枝
          • 后剪枝
          • Minimal Cost-Complexity Pruning 代价复杂剪枝（后剪枝算法）
      • CART - 最大基尼指数
      • 总结
      • 附：熵
      • • 熵的性质
  • 非参数概率密度统计模型
  • • Histogram
    • Parzen Kernel
    • Nadaraya-Watson
    • 高斯过程
    • • 算法目的
      • 算法理论要点
      • 实验
      • 附：高斯函数的基本性质
  • 特征工程
  • • 特征归一化
  • 集成学习
  • • 偏差与方差，欠拟合和过拟合
    • AUC
    • 集成学习类型
    • AdaBoosting
    • GBDT
    • SVM、逻辑回归、感知机
    • • 感知机
      • 逻辑回归
      • 线性可分SVM
      • 软间隔SVM：
      • Loss函数小结
  • 深度学习
  • • 神经网络基础
    • 梯度爆炸和梯度消失
    • • 梯度裁剪
    • RNN
    • • 采样
  • 线性代数
  • • 矩阵
    • • 矩阵的正定性
      • 特征值和特征向量
      • 特征值分解
      • 奇异值分解
    • 泰勒展开
    • • 一元函数的泰勒展开
      • 多元函数的泰勒展开
    • 雅可比矩阵
    • Hessian矩阵
  • 最优化
  • • 牛顿法
    • • 优点
      • 缺点
    • 拟牛顿法
    • 凸优化
    • • 凸集
      • 凸函数（Convexe）
    • 拉格朗日乘子法
    • KKT
  • 概率论
  • • 独立性
    • 强大数定律
    • 方差、协方差
    • • 例：Bagging为什么减少方差
    • 琴生不等式的证明
    • Gibbs不等式的证明
    • 中心极限定律
  • 聚类
  • • K-Means
    • EM

前言

本文旨在整理一些博主学习中零散的知识点。

决策树

决策树的目标是从一组样本数据中，根据不同的特征和属性，建立一棵树形的分类结构。从顶部根结点开始，所有样本聚在一起。经过根结点的划分，样本被分到不同的子结点中。再根据子结点的特征进一步划分，直至所有样本都被归到某一个类别（即叶结点）中。

直观上，分割的依据，是指分割后子结点的数据是否”纯“，即得益于某一个特征的分割，子数据集更加的同质。熵的值越小，则数据集的纯度越高。

例如百面机器学习中提到的例子，我们希望某一个子节点只包含”见“或者”不见“的信息。

常用的决策树算法有ID3、C4.5、CART，它们构建树所使用的启发式函数各是什么？除了构建准则之外，它们之间的区别与联系是什么？

ID3 - 最大信息增益

特征$A$对于数据集$D$的信息增益定义为
Gain ⁡ ( D , a ) = H ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ H ( D v ) \operatorname{Gain}(D, a)=H(D)-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} H\left(D^{v}\right) Gain(D,a)=H(D)−v=1∑V​∣D∣∣Dv∣​H(Dv)

ID3是采用信息增益作为评价标准，会倾向于取值较多的特征。因为，信息增益反映的是给定条件以后不确定性减少的程度，特征取值越多就意味着确定性更高，也就是条件熵越小，信息增益越大。

C4.5 - 最大信息增益比

g a i n R ( D , A ) = g ( D , A ) H A ( D ) gain_{R}(D, A)=\frac{g(D, A)}{H_{A}(D)} gainR​(D,A)=HA​(D)g(D,A)​
其中 H A ( D ) 是 H_{A}(D)是 HA​(D)是属性熵。
H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ log ⁡ 2 ∣ D i ∣ ∣ D ∣ , H_{A}(D)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \log _{2} \frac{\left|D_{i}\right|}{|D|}, HA​(D)=−i=1∑n​∣D∣∣Di​∣​log2​∣D∣∣Di​∣​,

相对于ID3算法的改进：

1. 用信息增益比来选择属性
2. 在决策树的构造过程中对树进行剪枝
3. 对连续数据也能处理
4. 能够对不完整数据进行处理

信息增益比

C4.5用属性熵对ID3的信息增量进行标准化。

在一定程度上可以避免ID3倾向于选择取值较多的属性作为节点的问题。
但是使用增益率可能产生另外一个问题，增益率可能会偏好取值比较少的属性。因此C4.5采用了一个启发式的算法，先从候选属性中找出高于平均水平的属性，再从高于平均水平的属性中选择增益率最高的属性。

处理连续数据

在ID3中，如何处理离散数据？我们自然可以想到将其拆分成若干个区间，然后用布尔值分割数据。问题是，如何选择最优的划分点？
C4.5的方法是：对于连续属性$a$（价格、年龄等）和数据集$D$，先对$a$的$n$个数值从小到大排列，两两计算中值$T$，然后根据$T$划分大于$T$或者小于$T$。穷举所有$T$，选择信息增益最大的$T$作为划分依据。

同样我们可以注意到，穷举中位数的过程的复杂度也是相当高的。

缺失值处理

• 如何在属性值缺失的情况下进行划分属性：计算每个样本的权重，即无缺失样本除以总样本数。

Gain ⁡ ( D , a ) = ρ × Gain ⁡ ( D ~ , a ) = ρ × ( Ent ⁡ ( D ~ ) − ∑ v = 1 V r ~ v Ent ⁡ ( D ~ v ) ) \begin{aligned} \operatorname{Gain}(D, a) &=\rho \times \operatorname{Gain}(\tilde{D}, a) \\ &=\rho \times\left(\operatorname{Ent}(\tilde{D})-\sum_{v=1}^{V} \tilde{r}_{v} \operatorname{Ent}\left(\tilde{D}^{v}\right)\right) \end{aligned} Gain(D,a)​=ρ×Gain(D~,a)=ρ×(Ent(D~)−v=1∑V​r~v​Ent(D~v))​

• 选定了划分属性，对于在该属性上缺失特征的样本的处理：

  若样本$x$在划分属性$a$上的取
  值未知，则将$x$同时划入所有子结点，且样本权值在与属性值 a v a^v av对应的子结点中调整为凡 r v ~ ⋅ w x \tilde{r_v}\cdot{w_x} rv​~​⋅wx​ ，直观地看，这就是让同一个样本以不同的概率划入到不同的子结点中去。

决策树剪枝

预剪枝

预剪枝要对划分前后的泛化性能进行估计。

1. 对于不能使验证集精度提高的分支，不再划分。
2. 当树到达一定深度的时候，不再划分。
3. 当到达当前结点样本数量过小时，不在划分。
   优点：降低过拟合，减少时间开销。
   缺点：局部无法提升精度并不代表之后的划分无法提升精度，因此有欠拟合风险。

后剪枝

先生成一颗完整的决策树。从叶结点向上地对所有非叶结点，根据是否提高泛化性能，决定是否剪去其子结点。

优点：降低过拟合，结果会通常比预剪枝更好。
缺点：时间开销更大。

Minimal Cost-Complexity Pruning 代价复杂剪枝（后剪枝算法）

算法步骤：

1. 从完整决策树T0开始，生成一个子树序列 T 0 , T 1 , T 2 , . . . , T n {T_0,T_1,T_2,...,T_n} T0​,T1​,T2​,...,Tn​，其中 T i + 1 T_{i+1} Ti+1​由 T i T_i Ti​生成， T n T_n Tn​为树的根结点。
2. 在子树序列中，根据真实误差选择最佳的决策树。

C α ( T ) = C ( T ) + α ∣ T ∣ C_{\alpha}(T)=C(T)+\alpha|T| Cα​(T)=C(T)+α∣T∣
参数$\alpha$：参数越大，最优子树越小，越欠拟合；参数越小，最优子树越大，越过拟合。$\alpha$等于0时，无需剪枝；趋于正无穷时，只保留根节点。

对于结点$t$剪枝阈值$g(t)$：
g ( t ) = C ( t ) − C ( T t ) ∣ T t ∣ − 1 g(t)=\frac{C(t)-C\left(T_{t}\right)}{\left|T_{t}\right|-1} g(t)=∣Tt​∣−1C(t)−C(Tt​)​
$\alpha$大于$g(t)$应该剪枝，剪枝会使整体损失函数减小；反之应该保留当前子树。

最后，只要用独立数据集测试子树序列，试试哪棵子树的误差最小就知道那棵是最好的方案了。

CART - 最大基尼指数

CART（Classification and Regression Tree，分类回归树）。

CART是一颗二叉树，采用二元切割法，每一步将数据，按特征A的取值切成两份，分别进入左右子树。
处理连续性变量：CART 由于其构建时每次都会对特征进行二值划分，因此可以很好地适用于连续性变量。
ID3和C4.5可以在每个结点上产生出多叉分支，且每个特征在层级之间不会复用。CART每个结点只会产生两个分支，因此最后会形成一颗二叉树，且每个特征可以被重复使用。
ID3和C4.5通过剪枝来权衡树的准确性与泛化能力，而CART直接利用全部数据发现所有可能的树结构进行对比。
回归树就用最小平方差。

总结

	是否可处理连续变量	是否容易过拟合	是否对缺失值敏感	是否可用于回归	是否允许特征重复
ID3	否	是	是	否	否
C4,5	是	否	否	否	否
CART	是	否	否	是	是

决策树是集成学习中常见的基分类器，因为：

• 决策树可以较为方便地将样本的权重整合到训练过程中。
• 决策树的表达能力和泛化能力，可以通过调节树的层数来做折中。
• 数据样本的扰动对于决策树的影响较大，因此不同子样本集合生成的决策树基分类器随机性较大，这样的“不稳定学习器”更适合作为基分类器（如随机森林）。

附：熵

熵最好理解为不确定性的量度，因为越随机的信源的熵越大。即越多的“不确定”，熵的值越大，则数据集的纯度越低。

H ( p ) = − ∑ k = 1 n p k l o g 2 p k H(p) = -\sum_{k=1}^np_klog_2p_k H(p)=−k=1∑n​pk​log2​pk​
设独立掷出$n$次骰子，每个面的概率彼此不相等。则获得序列 ( x 1 , x 2 , . . . x n ) (x_1,x_2,...x_n) (x1​,x2​,...xn​)的概率是
p ( ( x 1 , . . . , x n ) ) = ∏ i n p ( x i ) = ∏ k = 1 6 p k n k p((x_1,...,x_n)) = \prod_{i}^n p(x_i) = \prod_{k=1}^6p_k^{n_k} p((x1​,...,xn​))=i∏n​p(xi​)=k=1∏6​pknk​​
给定概率向量 p = ( p 1 , . . . , p n ) \bold{p} = (p_1,...,p_n) p=(p1​,...,pn​)，表示$n$个离散的概率分布， ∑ i = 1 n p i = 1 \sum_{i=1}^n p_i=1 ∑i=1n​pi​=1, p i > 0 p_i>0 pi​>0。当$n$趋于正无穷时，根据大数定理：
lim ⁡ n → ∞ n k = n p k p ( ( x 1 , . . . , x n ) ) = ∏ k = 1 6 p k n k = ∏ p k n k = 2 n ∑ p k l o g 2 p k = 2 − n H ( p ) \begin{aligned} \lim_{n\to \infty} n_k &= np_k \\ p((x_1,...,x_n)) &= \prod_{k=1}^6p_k^{n_k} \\ &= \prod p_k^{nk}\\ &= 2^{n\sum p_k log_2 p_k}\\ &= 2^{-nH(\bold{p})} \end{aligned} n→∞lim​nk​p((x1​,...,xn​))​=npk​=k=1∏6​pknk​​=∏pknk​=2n∑pk​log2​pk​=2−nH(p)​
$H(\mathbf{p})$越大，序列发生的概率就越小。反之，序列更有可能发生。

熵的性质

• $H(\mathbf{p})\ge 0$
• 给定 $\mathbf{p}$ 和 $\mathbf{q}$ 两个维度相等的概率向量，恒有：
  − ∑ i = i n p i l o g ( p i ) ≤ − ∑ i = 1 n p i l o g ( q i ) -\sum_{i=i}^n p_i log(p_i) \leq -\sum_{i=1}^n p_i log(q_i) −i=i∑n​pi​log(pi​)≤−i=1∑n​pi​log(qi​)
• $H(\mathbf{p})\le n$，$n$是$\mathbf{p}$的维度。

参考资料：

机器学习 - 周志华

决策树之C4.5算法

统计学习方法 - 李航

sklearn Decision Trees

集成学习复习笔记

非参数概率密度统计模型

Histogram

Parzen Kernel

Nadaraya-Watson

高斯过程

优

• 高斯过程可以直接推断目标函数的分布。
• 高斯过程非常适用于小数据集。
• 高斯过程也可用于分类问题。
• GPyTorch, sklearn等比较成熟的库

劣

• 在计算逆矩阵时，复杂度在 O ( n 3 ) O(n^3) O(n3)。甚至有时逆矩阵无法求解。
• 高斯过程假设数据满足多元正态分布和高斯噪声（有兴趣的读者可以谷歌 non gaussian likelihood）。

算法目的

求： P ( y ∗ ∣ D , x t ) P(y_*\mid D,\mathbf{x_t}) P(y∗​∣D,xt​)，即已知训练数据$D$，测试数据X_test x t \mathbf{x_t} xt​，求 y_test 的条件分布。

算法理论要点

高斯过程假设 y_train、y_test和每个向量的噪声先验服从高斯分布，即 [ y 1 y 2 ⋮ y n y t ] ∼ N ( 0 , Σ ) \begin{bmatrix} y_1\\ y_2\\ \vdots\\ y_n\\ y_t \end{bmatrix} \sim \mathcal{N}(0,\Sigma) ​y1​y2​⋮yn​yt​​ ​∼N(0,Σ) ϵ ∼ N ( 0 , σ y 2 I ) \boldsymbol\epsilon \sim \mathcal{N}(\mathbf{0}, \sigma_y^2 \mathbf{I}) ϵ∼N(0,σy2​I)

已知后验的 X_train，y_train，X_test数据，我们有：
μ y ∗ ∣ D = K ∗ T ( K + σ 2 I ) − 1 y Σ y ∗ ∣ D = K ∗ ∗ − K ∗ T ( K + σ 2 I ) − 1 K ∗ . \mu_{y_*\mid D} = K_*^T (K+\sigma^2 I)^{-1} y\\\Sigma_{y_*\mid D} = K_{**} - K_*^T (K+\sigma^2 I)^{-1}K_*. μy∗​∣D​=K∗T​(K+σ2I)−1yΣy∗​∣D​=K∗∗​−K∗T​(K+σ2I)−1K∗​.
最终结果
Y ∗ ∣ ( Y 1 = y 1 , . . . , Y n = y n , x 1 , . . . , x n ) ∼ N ( K ∗ ⊤ ( K + σ 2 I ) − 1 y , K ∗ ∗ + σ 2 I − K ∗ ⊤ ( K + σ 2 I ) − 1 K ∗ ) . Y_*|(Y_1=y_1,...,Y_n=y_n,\mathbf{x}_1,...,\mathbf{x}_n)\sim \mathcal{N}(K_*^\top (K+\sigma^2 I)^{-1}y,K_{**}+\sigma^2 I-K_*^\top (K+\sigma^2 I)^{-1}K_*). Y∗​∣(Y1​=y1​,...,Yn​=yn​,x1​,...,xn​)∼N(K∗⊤​(K+σ2I)−1y,K∗∗​+σ2I−K∗⊤​(K+σ2I)−1K∗​).

Σ i j = K ( x i , x j ) \Sigma_{ij}=K(\mathbf{x}_i,\mathbf{x}_j) Σij​=K(xi​,xj​)，$K$是核函数。表示数据点之间的相似度。

实验

源码可以在krasserm blog上获取。

先验

• X_test = np.arange(-5, 5, 0.2).reshape(-1, 1)，shape == (50,1)
• 中线蓝线为X_test的均值，高斯过程假设其处处为0。mu.shape == X_test.shape。
• X_test的协方差由核函数计算。cov.shape == (50,50)
• 蓝色区域称为不确定区域（uncertainty region，包含置信区间）。表示X_test每处数据点的方差浮动。数据点的方差越小，则我们越能确定其值的浮动区间。
• 三条从多元正态分布$\mathcal{N}(0,\Sigma )$抽取的样本，shape == (3,50)。**表示当前的y_test在均值为0，uncertainty region内上下浮动。y_test处处满足高斯分布。**有时曲线会超出不确定区域，这是因为不确定区域包含自定义的置信区间。

后验

• 后验过程，接受训练集X_train，y_train。对于每处X_train数据点（红色叉），限制其周围的不确定区域。我们可以观察到，样本Sample，即y_test，曲线能够活动的空间越来越小，在训练集足够多的情况下，可以基本确定y_test的曲线。即，此时y_test的每一个数据点，我们有较精确的概率分布$P$。

核

• RBF核/径向基函数核，参数$l$越大，越不容易过拟合。因为$l$越大，分母越大，$K$值越小，点和点之间的相似度越低。$l$取正无穷，则所有数据点都彼此不相关。

最大似然
log ⁡ p ( y ∣ X ) = log ⁡ N ( y ∣ 0 , K y ) = − 1 2 y T K y − 1 y − 1 2 log ⁡ ∣ K y ∣ − N 2 log ⁡ ( 2 π ) (11) \log p(\mathbf{y} \lvert \mathbf{X}) = \log \mathcal{N}(\mathbf{y} \lvert \boldsymbol{0},\mathbf{K}_y) = -\frac{1}{2} \mathbf{y}^T \mathbf{K}_y^{-1} \mathbf{y} -\frac{1}{2} \log \begin{vmatrix}\mathbf{K}_y\end{vmatrix} -\frac{N}{2} \log(2\pi) \tag{11} logp(y∣X)=logN(y∣0,Ky​)=−21​yTKy−1​y−21​log ​Ky​​ ​−2N​log(2π)(11)
公式可以用于计算score，也可以用最大似然法求导后优化参数。

附：高斯函数的基本性质

定义随机变量 y = [ y A y B ] , μ = [ μ A μ B ] Σ = [ Σ A A , Σ A B Σ B A , Σ B B ] y=\begin{bmatrix} y_A\\ y_B \end{bmatrix}, \mu=\begin{bmatrix} \mu_A\\ \mu_B \end{bmatrix}\Sigma=\begin{bmatrix} \Sigma_{AA}, \Sigma_{AB} \\ \Sigma_{BA}, \Sigma_{BB} \end{bmatrix} y=[yA​yB​​],μ=[μA​μB​​]Σ=[ΣAA​,ΣAB​ΣBA​,ΣBB​​]

1. ∫ y p ( y ; μ , Σ ) d y = 1 \int_y p(y;\mu,\Sigma)dy=1 ∫y​p(y;μ,Σ)dy=1
2. 边际分布 p ( y A ) = ∫ y B p ( y A , y B ; μ , Σ ) d y B p(y_A)=\int_{y_B}p(y_A,y_B;\mu,\Sigma)dy_B p(yA​)=∫yB​​p(yA​,yB​;μ,Σ)dyB​ 和 p ( y B ) = ∫ y A p ( y A , y B ; μ , Σ ) d y A p(y_B)=\int_{y_A}p(y_A,y_B;\mu,\Sigma)dy_A p(yB​)=∫yA​​p(yA​,yB​;μ,Σ)dyA​ 满足高斯分布。 y A ∼ N ( μ A , Σ A A ) y B ∼ N ( μ B , Σ B B ) . y_A\sim \mathcal{N}(\mu_A,\Sigma_{AA})\\y_B\sim \mathcal{N}(\mu_B,\Sigma_{BB}). yA​∼N(μA​,ΣAA​)yB​∼N(μB​,ΣBB​).
3. 两个高斯函数相加仍为高斯函数。均值相加，方差相加。
4. y A y_A yA​ 和 y B y_B yB​ 的条件分布仍为高斯分布 p ( y A ∣ y B ) = p ( y A , y B ; μ , Σ ) ∫ y A p ( y A , y B ; μ , Σ ) d y A , y A ∣ y B = y B ∼ N ( μ A + Σ A B Σ B B − 1 ( y B − μ B ) , Σ A A − Σ A B Σ B B − 1 Σ B A ) . p(y_A|y_B)=\frac{p(y_A,y_B;\mu,\Sigma)}{\int_{y_A}p(y_A,y_B;\mu,\Sigma)dy_A},\\y_A|y_B=y_B\sim \mathcal{N}(\mu_A+\Sigma_{AB}\Sigma_{BB}^{-1}(y_B-\mu_B),\Sigma_{AA}-\Sigma_{AB}\Sigma_{BB}^{-1}\Sigma_{BA}). p(yA​∣yB​)=∫yA​​p(yA​,yB​;μ,Σ)dyA​p(yA​,yB​;μ,Σ)​,yA​∣yB​=yB​∼N(μA​+ΣAB​ΣBB−1​(yB​−μB​),ΣAA​−ΣAB​ΣBB−1​ΣBA​).

Ref : krasserm blog
cs.cornell.edu/courses/cs4780/

参考资料：七种常用回归技术，如何正确选择回归模型？

特征工程

特征归一化

对数值类型的特征做归一化可以将所有的特征都统一到一个大致相同的数值区间内。

1. 线性函数归一化（Min-Max Scaling）。它对原始数据进行线性变换，使结果映射到[0, 1]的范围。
   X n o r m = X − X m i n X m a x − X m i n X_{norm} = \frac{X - X_{min}}{X_{max} - X_{min}} Xnorm​=Xmax​−Xmin​X−Xmin​​
2. 零均值归一化（Z-Score Normalization）。它会将原始数据映射到均值为0、标准差为1的分布上。 z = x − μ σ z = \frac {x-\mu}{\sigma} z=σx−μ​

需要归一化的模型： 线性回归、逻辑回归、SVM、NN。
不需要归一化的模型：决策树（信息增益和特征是否经过归一化无关）。

参考资料：百面机器学习

集成学习

偏差与方差，欠拟合和过拟合

• 偏差指预测输出与真实标记的差别，偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
• 方差指一个特定训练集训练得到的函数，与所有训练集得到平均函数的差的平方再取期望。方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。方差表示所有模型构建的预测函数，与真实函数的差别有多大。
• 欠拟合指模型不够复杂或者训练数据过少时，模型均无法捕捉训练数据的基本(或者内在)关系，会出现偏差。
• 过拟合指模型过于复杂或者没有足够的数据支持模型的训练时，模型含有训练集的特有信息，对训练集过于依赖，即模型会对训练集高度敏感，这种现象称之为模型过拟合。

参考资料：偏差与方差，欠拟合与过拟合

AUC

随机给定一个正样本和一个负样本，分类器输出该正样本为正的那个概率值比分类器输出该负样本为正的那个概率值要大的可能性。
如何理解机器学习和统计中的AUC？

集成学习类型

• Boosting，它的基本思路是将基分类器层层叠加，每一层在训练的时候，对前一层基分类器分错的样本，给予更高的权重。测试时，根据各层分类器的结果的加权得到最终结果。
  减少偏差，减少欠拟合。Boosting方法是通过逐步聚焦于基分类器分错的样本，减小集成分类器的偏差。
• Bagging，减少方差，减少过拟合。通过对训练样本多次采样，并分别训练出多个不同模型，然后做综合，来减小集成分类器的方差。

AdaBoosting

Adaboost对分类正确的样本降低了权重，对分类错误的样本升高或者保持权重不变。在最后进行模型融合的过程中，也根据错误率对基分类器进行加权融合。错误率低的分类器拥有更大的“话语权”。

GBDT

Gradient Boosting是Boosting中的一大类算法，其基本思想是根据当前模型损失函数的负梯度信息来训练新加入的弱分类器，然后将训练好的弱分类器以累加的形式结合到现有模型中。

优点：

• 预测阶段速度快并且可并行
• 在分布稠密的数据集上，泛化能力和表达能力都很好。
• 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性，能够自动发现特征间的高阶关系，并且也不需要对数据进行特殊的预处理如归一化等。

缺点：

• GBDT在高维稀疏的数据集上，表现不如支持向量机或者神经网络。
• GBDT在处理文本分类特征问题上，相对其他模型的优势不如它在处理数值特征时明显。
• 训练过程需要串行训练，只能在决策树内部采用一些局部并行的手段提高训练速度。

SVM、逻辑回归、感知机

感知机

决策函数：
$$f(x)=\mathrm{sign}(w\cdot x+b)$$
Loss函数：
$$L(y,f(x))=\max (0,yf(x))$$
损失函数：
− ∑ x i ∈ M y i ( w ⋅ x i + b ) -\sum_{x_{i} \in M} y_{i}\left(w \cdot x_{i}+b\right) −xi​∈M∑​yi​(w⋅xi​+b)
学习过程：
随机梯度下降，只对误分类点更新参数。

逻辑回归

考虑对输入$x$进行分类的线性函数$wx$，用逻辑函数将$wx$转换为概率，则有决策函数：
P ( Y = 1 ∣ x ) = exp ⁡ ( w ⋅ x ) 1 + exp ⁡ ( w ⋅ x ) P(Y=1 \mid x)=\frac{\exp (w \cdot x)}{1+\exp (w \cdot x)} P(Y=1∣x)=1+exp(w⋅x)exp(w⋅x)​
$wx$越大，概率趋于1；$wx$越小，概率越接近0。

损失函数：
L ( y ^ , y ) = − y log ⁡ ( y ^ ) − ( 1 − y ) log ⁡ ( 1 − y ^ ) L(\hat{y}, y)=-y \log (\hat{y})-(1-y) \log (1-\hat{y}) L(y^​,y)=−ylog(y^​)−(1−y)log(1−y^​)
最大似然估计：
L ( w ) = ∑ [ y i ln ⁡ p ( x i ) + ( 1 − y i ) ln ⁡ ( 1 − p ( x i ) ) ] = ∑ [ y i ln ⁡ p ( x i ) 1 − p ( x i ) + ln ⁡ ( 1 − p ( x i ) ) ] = ∑ [ y i ( w ⋅ x i ) − ln ⁡ ( 1 + e w ⋅ x i ) ] \begin{aligned} L(w) &=\sum\left[y_{i} \ln p\left(x_{i}\right)+\left(1-y_{i}\right) \ln \left(1-p\left(x_{i}\right)\right)\right] \\ &=\sum\left[y_{i} \ln \frac{p\left(x_{i}\right)}{1-p\left(x_{i}\right)}+\ln \left(1-p\left(x_{i}\right)\right)\right] \\ &=\sum\left[y_{i}\left(w \cdot x_{i}\right)-\ln \left(1+e^{w \cdot x_{i}}\right)\right] \end{aligned} L(w)​=∑[yi​lnp(xi​)+(1−yi​)ln(1−p(xi​))]=∑[yi​ln1−p(xi​)p(xi​)​+ln(1−p(xi​))]=∑[yi​(w⋅xi​)−ln(1+ew⋅xi​)]​

线性可分SVM

分类决策函数：
f ( x ) = sign ⁡ ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right) f(x)=sign(w∗⋅x+b∗)
或者：
f ( x ) = ∑ i = 1 m α i y ( i ) K ( x ( i ) , x ) + b f(x)=\sum_{i=1}^{m} \alpha_{i} y^{(i)} K\left(x^{(i)}, x\right)+b f(x)=i=1∑m​αi​y(i)K(x(i),x)+b
Loss函数：
$$L(y,f(x))=\max (0,1-yf(x))$$
约束最优化方程：
min ⁡ w , b 1 2 ∥ w ∥ 2 s.t.  y i ( w ⋅ x i + b ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \end{array} minw,b​ s.t. ​21​∥w∥2yi​(w⋅xi​+b)−1⩾0,i=1,2,⋯,N​
拉格朗日对偶：
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(w \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i} L(w,b,α)=21​∥w∥2−i=1∑N​αi​yi​(w⋅xi​+b)+i=1∑N​αi​
$w$的求值和支持向量：
w ∗ = ∑ i α i ∗ y i x i w^{*}=\sum_{i} \alpha_{i}^{*} y_{i} x_{i} w∗=i∑​αi∗​yi​xi​
大多数$\alpha$值为0，只有少数的 ( y i , x i ) (y_{i}, x_{i}) (yi​,xi​)的系数$\alpha$不为0。这些点落在边界上，被称为支持向量。我们用这些点代入求解$w$。

软间隔SVM：

对于线性不可分的数据集，SVM假设存在一些离群点（outlier）。除去特异点后，剩下的数据点线性可分。
线性不可分意味着有些样本点不能满足限制条件 s.t.  y i ( w ⋅ x i + b ) − 1 ⩾ 0 \text { s.t. } y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0  s.t. yi​(w⋅xi​+b)−1⩾0，此时引入 ξ i \xi_{i} ξi​进行松弛。
min ⁡ w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i s.t.  y i ( w ⋅ x i + b ) ⩾ 1 − ξ i , i = 1 , 2 , ⋯ , N ξ i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{array}{ll} \min _{w, b, \xi} & \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{N} \xi_{i} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant 1-\xi_{i}, \quad i=1,2, \cdots, N \\ & \xi_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array} minw,b,ξ​ s.t. ​21​∥w∥2+C∑i=1N​ξi​yi​(w⋅xi​+b)⩾1−ξi​,i=1,2,⋯,Nξi​⩾0,i=1,2,⋯,N​

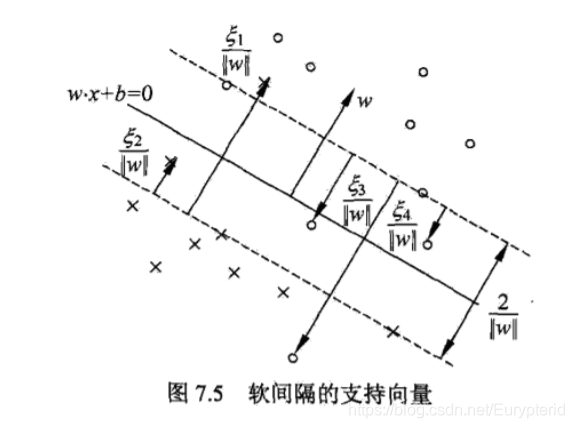
由KKT得，若 α ∗ < C \alpha^* < C α∗<C，支持向量落在边界上。

SVM算法的主要优点有：

• 解决高维特征的分类问题和回归问题很有效，在特征维度大于样本数时依然有很好的效果。
• 仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。
• 有大量的核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题。
• 样本量不是海量数据的时候，分类准确率高，泛化能力强。

SVM算法的主要缺点有：

• 如果特征维度远远大于样本数，则SVM表现一般。
• SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。
• 非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数。
• SVM对缺失数据敏感。

参考资料：
统计学习方法

Loss函数小结

	感知机	SVM	逻辑回归
Loss函数	Hinge Loss变种	Hinge Loss	交叉熵
特点	只关注误分类点，分类对就行	对判定边界的点惩罚力度很高	误差大的时候，权重更新快；误差小的时候，权重更新慢。在用sigmoid作为激活函数时，比MSE更好

深度学习

神经网络基础

一般来说：

• 在一个隐含层中加更多的神经元，提高了当前隐含层的表达力，相当于增加了当前维度的特征。
• 添加多个隐含层，相当于聚合之前隐含层的特征，并输出高维的特征组合。
• 无论上述哪种方式，都能增加模型表达力，朝着过拟合的方向移动。

梯度爆炸和梯度消失

梯度裁剪

可以将梯度限制在某个区间$[-clip\_value,clip\_value]$内，以防止梯度爆炸。

参考资料：
深度炼丹之梯度裁剪

RNN

采样

线性代数

矩阵

矩阵的正定性

一个$n\times n$的对称矩阵（方阵）$A$是正定的，当且仅当对任意非零向量$x$，满足：
x T A x > 0 x^TAx > 0 xTAx>0
一般通过矩阵的特征值判断矩阵是否正定。特征值全大于0，则矩阵正定。

特征值和特征向量

若向量$\mathrm{x}$和实数$\lambda$满足
$$\begin{gathered} \mathrm{Ax}=\lambda \mathrm{x} \\ (\mathrm{A}-\lambda \mathrm{I})\mathrm{x}=0 \end{gathered}$$
则称$\mathrm{x}$为特征向量，$\lambda$为特征值。
矩阵的阶数小于5时，通过行列式：
$$|\mathrm{A}-\lambda \mathrm{I}|=0$$
求解方程。

另外，有：
tr ⁡ ( A ) = ∑ i = 1 n a i i ∏ i = 1 n λ i = ∣ A ∣ \operatorname{tr}(\mathrm{A})=\sum_{i=1}^{n} a_{i i} \\ \prod_{i=1}^{n} \lambda_{i}=|\mathrm{A}| tr(A)=i=1∑n​aii​i=1∏n​λi​=∣A∣

特征值分解

设方阵$A$维度为$n$， x i \mathrm x_i xi​是它的特征向量且互相线性无关。$n$个特征向量按列组成矩阵$P$（若$det(P)\ne 0$则向量线性无关）。$D$为所有特征值$\lambda$填充在对角线上的$n$维矩阵。
则有公式：
A = P D P − 1 A = PDP^{-1} A=PDP−1
若$P$是正交矩阵，则$P$满足：
P − 1 = P T P^{-1} = P^T P−1=PT
则有：
A = P D P T A = PDP^{T} A=PDPT

奇异值分解

特征值分解只适用于方阵，对于一个$m\times n$的矩阵$A$，其分解为：
A = U Σ V T A = U\Sigma V^T A=UΣVT
其中$U,V$为正交矩阵，$\Sigma$为对角矩阵，且：
U = A A T V = A T A U = AA^T \\ V = A^TA U=AATV=ATA

泰勒展开

一元函数的泰勒展开

f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 f ′ ′ ( x 0 ) ( x − x 0 ) 2 + … + 1 n ! f ( n ) ( x 0 ) ( x − x 0 ) n … f(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{0}\right)\left(x-x_{0}\right)^{2}+\ldots+\frac{1}{n !} f^{(n)}\left(x_{0}\right)\left(x-x_{0}\right)^{n} \ldots f(x)=f(x0​)+f′(x0​)(x−x0​)+21​f′′(x0​)(x−x0​)2+…+n!1​f(n)(x0​)(x−x0​)n…
（随机）梯度下降为一阶展开，牛顿法为二阶展开。

多元函数的泰勒展开

f ( x ) = f ( x 0 ) + ( ∇ f ( x 0 ) ) T ( x − x 0 ) + 1 2 ( x − x 0 ) T ∇ 2 f ( x 0 ) ( x − x 0 ) + o ( ∥ x − x 0 ∥ 2 ) f(\mathrm{x})=f\left(\mathrm{x}_{0}\right)+\left(\nabla f\left(\mathrm{x}_{0}\right)\right)^{\mathrm{T}}\left(\mathrm{x}-\mathrm{x}_{0}\right)+\frac{1}{2}\left(\mathrm{x}-\mathrm{x}_{0}\right)^{\mathrm{T}}\nabla ^2 f(x_0)(x-x_0)+o\left(\left\|\mathrm{x}-\mathrm{x}_{0}\right\|^{2}\right) f(x)=f(x0​)+(∇f(x0​))T(x−x0​)+21​(x−x0​)T∇2f(x0​)(x−x0​)+o(∥x−x0​∥2)

雅可比矩阵

y = f ( x ) y i = f i ( x ) [ ∂ y 1 ∂ x 1 ∂ y 1 ∂ x 2 … ∂ y 1 ∂ x n ∂ y 2 ∂ x 1 ∂ y 2 ∂ x 2 … ∂ y 2 ∂ x n … … … … ∂ y m ∂ x 1 ∂ y m ∂ x 2 … ∂ y m ∂ x n ] \begin{array}{l} \mathrm{y}=f(\mathrm{x}) \quad y_{i}=f_{i}(\mathrm{x}) \\ {\left[\begin{array}{cccc} \frac{\partial y_{1}}{\partial x_{1}} & \frac{\partial y_{1}}{\partial x_{2}} & \ldots & \frac{\partial y_{1}}{\partial x_{n}} \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} & \ldots & \frac{\partial y_{2}}{\partial x_{n}} \\ \ldots & \ldots & \ldots & \ldots \\ \frac{\partial y_{m}}{\partial x_{1}} & \frac{\partial y_{m}}{\partial x_{2}} & \ldots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right]} \end{array} y=f(x)yi​=fi​(x) ​∂x1​∂y1​​∂x1​∂y2​​…∂x1​∂ym​​​∂x2​∂y1​​∂x2​∂y2​​…∂x2​∂ym​​​…………​∂xn​∂y1​​∂xn​∂y2​​…∂xn​∂ym​​​ ​​
矩阵在位置$(i,j)$的值为 ∂ y i ∂ x j \frac{\partial{y_i}}{{\partial{x_j}}} ∂xj​∂yi​​。矩阵维度为$(m,n)$。

Hessian矩阵

[ ∂ 2 f ∂ x 1 2 ∂ 2 f ∂ x 1 ∂ x 2 … ∂ 2 f ∂ x 1 ∂ x n ∂ 2 f ∂ x 2 ∂ x 1 ∂ 2 f ∂ x 2 2 ⋯ ∂ 2 f ∂ x 2 ∂ x n ⋯ ⋯ ⋯ ⋯ ∂ 2 f ∂ x n ∂ x 1 ∂ 2 f ∂ x n ∂ x 2 ⋯ ∂ 2 f ∂ x n 2 ] \left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \ldots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \cdots & \cdots & \cdots & \cdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] ​∂x12​∂2f​∂x2​∂x1​∂2f​⋯∂xn​∂x1​∂2f​​∂x1​∂x2​∂2f​∂x22​∂2f​⋯∂xn​∂x2​∂2f​​…⋯⋯⋯​∂x1​∂xn​∂2f​∂x2​∂xn​∂2f​⋯∂xn2​∂2f​​ ​
Hessian矩阵一般用于判断多元函数的极值。若点$z$满足 f ′ ( z ) = 0 f^{\prime}(z) = 0 f′(z)=0，且Hessian矩阵为正定，则函数在该点有极小值；负定则有极大值。
Hessian矩阵正定等价于 f ′ ′ ( x ) > 0 f^{\prime\prime}(x) > 0 f′′(x)>0；负定则反之。

Hessian矩阵是对称矩阵。
如果Hessian矩阵正定，则$f$是凸函数；负定：凹函数。

最优化

牛顿法

将多元函数的展开到二次，对$\mathrm{x}$向量求导，最后得到：
x = x 0 − ϵ H − 1 ∇ f ( x 0 ) \mathrm x = \mathrm x_0 - \epsilon H^{-1}\nabla f(\mathrm x_0) x=x0​−ϵH−1∇f(x0​)
H ≡ ∇ 2 f ( x 0 ) H \equiv \nabla^2 f(\mathrm x_0) H≡∇2f(x0​)
$H$是$f$在 x 0 \mathrm x_0 x0​处的Hessian矩阵。

优点

• 二次展开收敛速度通常更快

缺点

• Hessian矩阵的逆有时无法求解；或者求解过程开销大
• $ϵ$参数无法固定，每次更新需要用Line Search的方式选优，增大了复杂度

拟牛顿法

凸优化

凸集

凸函数（Convexe）

对于任意 x 1 , x 2 \mathbf{x}_{1}, \mathbf{x}_{2} x1​,x2​和$\alpha ，0<\alpha <1$，函数$f(x)$满足
f [ α x 1 + ( 1 − α ) x 2 ] ≤ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) f\left[\alpha \mathbf{x}_{1}+(1-\alpha) \mathbf{x}_{2}\right] \leq \alpha f\left(\mathbf{x}_{1}\right)+(1-\alpha) f\left(\mathbf{x}_{2}\right) f[αx1​+(1−α)x2​]≤αf(x1​)+(1−α)f(x2​)
则$f(x)$是凸函数。

若 x 1 ≠ x 2 \mathbf{x}_{1}\neq \mathbf{x}_{2} x1​=x2​，则$f(x)$是严格凸的。

拉格朗日乘子法

L ( x , λ , μ ) = f ( x ) + ∑ i λ i c i ( x ) + ∑ j μ j g j ( x ) \mathcal{L}(\mathbf{x}, \boldsymbol{\lambda}, \boldsymbol{\mu})=f(\mathbf{x})+\sum_{i} \lambda_{i} c_{i}(\mathbf{x})+\sum_{j} \mu_{j} g_{j}(\mathbf{x}) L(x,λ,μ)=f(x)+i∑​λi​ci​(x)+j∑​μj​gj​(x)
其中$g(x)$为不等式约束，$c(x)$为等式约束。

$f(x)$为凸函数时，满足：
f ( x ∗ ) = max ⁡ μ , λ min ⁡ x L ( μ , λ , x ) = min ⁡ x max ⁡ μ , λ L ( μ , λ , x ) = f ( x ∗ ) f\left(x^{*}\right)=\max _{\mu, \lambda} \min _{x} L(\mu, \lambda, x)=\min _{x} \max _{\mu, \lambda} L(\mu, \lambda, x)=f\left(x^{*}\right) f(x∗)=μ,λmax​xmin​L(μ,λ,x)=xmin​μ,λmax​L(μ,λ,x)=f(x∗)

KKT

1. ∇ L ( x ∗ , λ ∗ , μ ∗ ) = 0 \nabla \mathcal L(\mathbf x^*, \mathbf \lambda^*, \mathbf \mu^*) = 0 ∇L(x∗,λ∗,μ∗)=0
2. ∀ i c i ( x ∗ ) ≤ 0 , ∀ j g j ( x ∗ ) = 0 \forall i \space c_{i}\left(\mathbf{x}^{*}\right) \leq 0, \forall j \space g_{j}\left(\mathbf{x}^{*}\right)=0 ∀i ci​(x∗)≤0,∀j gj​(x∗)=0
3. ∀ i λ i ∗ ≥ 0 \forall i \space \lambda_{i}^{*} \geq 0 ∀i λi∗​≥0
4. λ i ∗ c i ( x ∗ ) = 0 \lambda_{i}^{*} c_{i}\left(\mathbf{x}^{*}\right)=0 λi∗​ci​(x∗)=0：若 c i ( x ∗ ) < 0 c_{i}\left(\mathbf{x}^{*}\right)<0 ci​(x∗)<0，则 λ i = 0 \lambda_i = 0 λi​=0；否则 λ i > 0 \lambda_i >0 λi​>0且 c i ( x ∗ ) = 0 c_{i}\left(\mathbf{x}^{*}\right)=0 ci​(x∗)=0。

概率论

独立性

• 两两独立：$P(AB)=P(A)\ast P(B)$
• 互相独立：$P(ABC)=P(A)\ast P(B)\ast P(C)$即一组事件的发生不会影响另一组（或一个）事件的发生。

强大数定律

已知 ( X n ) n ∈ N (X_n)_n\in\N (Xn​)n​∈N随机变量序列并服从相同的分布，且变量和变量之间两两独立，则均值（也称试验均值）
X ˉ n = ∑ k = 1 n X k n \bar{X}_{n}=\frac{\sum_{k=1}^{n} X_{k}}{n} Xˉn​=n∑k=1n​Xk​​
收敛于其数学期望。即：
E ( X ˉ n ) = m E\left(\bar{X}_{n}\right)=m E(Xˉn​)=m
同时有：
V ( X ˉ n ) = σ 2 n V\left(\bar{X}_{n}\right)=\frac{\sigma^{2}}{n} V(Xˉn​)=nσ2​

弱大数定律不能保证处处收敛，只能保证依概率收敛。

给定概率向量 p = ( p 1 , . . . , p n ) \bold{p} = (p_1,...,p_n) p=(p1​,...,pn​)，表示$n$个离散的概率分布， ∑ i = 1 n p i = 1 \sum_{i=1}^n p_i=1 ∑i=1n​pi​=1, p i > 0 p_i>0 pi​>0。当$n$趋于正无穷时，根据大数定理：
lim ⁡ n → ∞ n k = n p k \lim_{n\to \infty} n_k = np_k n→∞lim​nk​=npk​

方差、协方差

$\mu ,\nu$是数学期望值，大数定律下趋于均值。
Var ⁡ ( X ) = E [ ( X − μ ) 2 ] = ∑ ( x i − E ( x ) ) 2 p ( x i ) Var ⁡ ( X ) = E ( X 2 ) − E ( X ) 2 Var ⁡ ( X + a ) = Var ⁡ ( X ) Var ⁡ ( a X ) = a 2 Var ⁡ ( X ) Var ⁡ ( a X + b Y ) = a 2 Var ⁡ ( X ) + b 2 Var ⁡ ( Y ) + 2 a b Cov ⁡ ( X , Y ) , Var ⁡ ( X − Y ) = Var ⁡ ( X ) + Var ⁡ ( Y ) − 2 Cov ⁡ ( X , Y ) Var ⁡ ( ∑ i = 1 N X i ) = ∑ i , j = 1 N Cov ⁡ ( X i , X j ) = ∑ i = 1 N Var ⁡ ( X i ) + ∑ i ≠ j Cov ⁡ ( X i , X j ) \operatorname{Var}(X)=\mathrm{E}\left[(X-\mu)^{2}\right] = \sum (x_i - E(x))^2 p(x_i) \\ \operatorname{Var}(X)=\mathrm{E}\left(X^{2}\right)-\mathrm{E}(X)^{2}\\ \operatorname{Var}(X+a)=\operatorname{Var}(X) \\ \operatorname{Var}(a X)=a^{2} \operatorname{Var}(X) \\ \begin{array}{l} \operatorname{Var}(a X+b Y)=a^{2} \operatorname{Var}(X)+b^{2} \operatorname{Var}(Y)+2 a b \operatorname{Cov}(X, Y), \\ \operatorname{Var}(X-Y)=\operatorname{Var}(X)+\operatorname{Var}(Y)-2 \operatorname{Cov}(X, Y) \end{array}\\ \operatorname{Var}\left(\sum_{i=1}^{N} X_{i}\right)=\sum_{i, j=1}^{N} \operatorname{Cov}\left(X_{i}, X_{j}\right)=\sum_{i=1}^{N} \operatorname{Var}\left(X_{i}\right)+\sum_{i \neq j} \operatorname{Cov}\left(X_{i}, X_{j}\right) Var(X)=E[(X−μ)2]=∑(xi​−E(x))2p(xi​)Var(X)=E(X2)−E(X)2Var(X+a)=Var(X)Var(aX)=a2Var(X)Var(aX+bY)=a2Var(X)+b2Var(Y)+2abCov(X,Y),Var(X−Y)=Var(X)+Var(Y)−2Cov(X,Y)​Var(i=1∑N​Xi​)=i,j=1∑N​Cov(Xi​,Xj​)=i=1∑N​Var(Xi​)+i=j∑​Cov(Xi​,Xj​)
$$\mathrm{cov}(X,Y)=\mathrm{E}((X-\mu )(Y-\nu ))=\mathrm{E}(X\cdot Y)-\mu \nu$$

例：Bagging为什么减少方差

Bagging对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。
在各子模型独立，变量完全无关的情况下，有：
∑ i ≠ j Cov ⁡ ( X i , X j ) = 0 \sum_{i \neq j} \operatorname{Cov}\left(X_{i}, X_{j}\right) = 0 i=j∑​Cov(Xi​,Xj​)=0
则：
V ( ∑ i = 1 n X i n ) = 1 n 2 V ( ∑ i = 1 n X i ) = 1 n 2 ∑ i = 1 n V ( X i ) V\left(\frac{\sum_{i=1}^{n} X_{i}}{n}\right)=\frac{1}{n^{2}} V\left(\sum_{i=1}^{n} X_{i}\right)=\frac{1}{n^{2}} \sum_{i=1}^{n} V\left(X_{i}\right) V(n∑i=1n​Xi​​)=n21​V(i=1∑n​Xi​)=n21​i=1∑n​V(Xi​)
同理，若各子模型完全相同，则：
V ( ∑ i = 1 n X i n ) = V ( n ∗ X i n ) = V ( X i ) V\left(\frac{\sum_{i=1}^{n} X_{i}}{n}\right)=V\left(\frac{n * X_{i}}{n}\right)=V\left(X_{i}\right) V(n∑i=1n​Xi​​)=V(nn∗Xi​​)=V(Xi​)
无法降低方差。

参考：
知乎

琴生不等式的证明

若$f$是可导的凸函数，$\mathbf{p}$为概率向量 p = ( p 1 , . . . , p n ) \bold{p} = (p_1,...,p_n) p=(p1​,...,pn​)，表示$n$个离散的概率分布，和 t i t_i ti​任意实数。已知KL距离 D ( p ∥ q ) = ∑ i = 1 n p i log ⁡ ( p i q i ) 。 D(\mathbf{p} \| \mathbf{q})=\sum_{i=1}^{n} p_{i} \log \left(\frac{p_{i}}{q_{i}}\right)。 D(p∥q)=∑i=1n​pi​log(qi​pi​​)。用数学归纳法证明： ∑ i = 1 n p i f ( t i ) ≥ f ( ∑ i = 1 n p i t i ) \sum_{i=1}^{n} p_{i} f\left(t_{i}\right) \geq f\left(\sum_{i=1}^{n} p_{i} t_{i}\right) i=1∑n​pi​f(ti​)≥f(i=1∑n​pi​ti​)
依据凸函数的定义，$n=2$时不等式成立。
设$n-1$时不等式成立，证明$n$时不等式仍然成立：
令 p i ′ = p i 1 − p n p_i^{\prime}=\frac{p_i}{1-p_n} pi′​=1−pn​pi​​
f ( ∑ i = 1 n p i t i ) = f ( ∑ i = 1 n − 1 p i t i + p n t n ) = f ( ( 1 − p n ) ∑ i = 1 n − 1 p i ′ t i + p n t n ) ≤ ( 1 − p n ) f ( ∑ i = 1 n − 1 p i ′ t i ) + p n f ( t n ) ≤ ( 1 − p n ) ∑ i = 1 n − 1 p i ′ f ( t i ) + p n f ( t n ) ，因为 n − 1 时不等式成立 = ∑ i = 1 n p i f ( t i ) \begin{aligned} f(\sum_{i=1}^{n}p_it_i) &= f(\sum_{i=1}^{n-1} p_it_i + p_nt_n) \\ &= f((1-p_n)\sum_{i=1}^{n-1} p_i^{\prime}t_i + p_nt_n) \\ &\leq (1-p_n)f(\sum_{i=1}^{n-1} p_i^{\prime}t_i) + p_nf(t_n)\\ &\leq (1-p_n)\sum_{i=1}^{n-1} p_i^{\prime}f(t_i) + p_nf(t_n)，因为n-1时不等式成立\\ &= \sum_{i=1}^{n} p_{i} f\left(t_{i}\right) \end{aligned} f(i=1∑n​pi​ti​)​=f(i=1∑n−1​pi​ti​+pn​tn​)=f((1−pn​)i=1∑n−1​pi′​ti​+pn​tn​)≤(1−pn​)f(i=1∑n−1​pi′​ti​)+pn​f(tn​)≤(1−pn​)i=1∑n−1​pi′​f(ti​)+pn​f(tn​)，因为n−1时不等式成立=i=1∑n​pi​f(ti​)​
证毕。

Gibbs不等式的证明

若$\mathbf{p}，\mathbf{q}$两个相同维度的概率向量，证明： ∑ i = 1 n p i log ⁡ ( p i ) ≥ ∑ i = 1 n p i log ⁡ ( q i ) \sum_{i=1}^{n} p_i\log(p_i) \geq \sum_{i=1}^{n} p_i\log{(q_i)} i=1∑n​pi​log(pi​)≥i=1∑n​pi​log(qi​)
由：
$\log (x)$为凹函数，则$-\log (x)$为凸函数。
有：
0 = − log ⁡ ∑ q i = − log ⁡ ∑ p i q i p i ≤ ∑ p i ( − log ⁡ q i p i ) = − ∑ p i log ⁡ q i p i \begin{aligned} 0 = -\log{\sum{q_i}} &= -\log{\sum{p_i}\frac{q_i}{p_i}}\\ &\leq \sum{p_i}(-\log{q_i}{p_i})\\ &=-\sum{p_i}\log{\frac{q_i}{p_i}} \end{aligned} 0=−log∑qi​​=−log∑pi​pi​qi​​≤∑pi​(−logqi​pi​)=−∑pi​logpi​qi​​​
所以
− ∑ p i log ⁡ q i p i ≥ 0 -\sum{p_i}\log{\frac{q_i}{p_i}} \geq 0 −∑pi​logpi​qi​​≥0
化简后即得到Gibbs不等式。证毕。

参考资料：
漫步最优化十四——凸函数与凹函数

中心极限定律

试验均值收敛于正态分布：
X ˉ n − μ σ / n → N ( 0 , 1 ) \frac{\bar{X}_{n}-\mu}{\sigma / \sqrt{n}} {\rightarrow} \mathcal{N}(0,1) σ/n ​Xˉn​−μ​→N(0,1)

参考资料：
阿里天池 - 人工智能的数学基础

聚类

K-Means

EM

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！