【知识点】(一)函数
目录
- 函数
- 1. 垂线检验函数
- 2. 求定义域
- 3. 求值域
- 反函数
- 1. 水平线检验反函数
- 2. 求反函数
- 3. 限制定义域
- 常见函数及图像
- 1. 线性函数
- 2. 多项式函数
- 3. 有理函数
- 4. 指数函数和对数函数
- 5. 绝对值函数
- 函数基本特性
- 1. 复合、奇函数和偶函数
- 2. 单调函数
- 3. 周期函数
- 4. 有界函数
- 三角函数
- 1. 弧度和三角函数
- 2. 三角函数的值
- 3. 三角函数的图像
- 4. 三角恒等式
- 参考资料
函数
函数 f f f:对象转化规则。 \quad f ( x ) f(x) f(x):函数 f f f 应用于对象 x x x \quad 区间表示法: [ a , b ] [a,b] [a,b]
1. 垂线检验函数
如果存在落在 x x x 轴的垂线和图像相交多于一次,那么该图像不是函数图像。
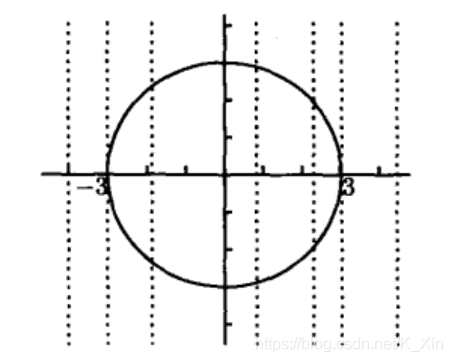
2. 求定义域
(1) 分母不为 0 0 0;(2) 负数不能取平方根; (3) 负数和零不能取对数
3. 求值域
画出函数图像,想象从图像左右两侧朝 y y y 轴水平射入两束光纤,曲线会在 y y y 轴左右两侧留下影子,值域 就是影子的并集。
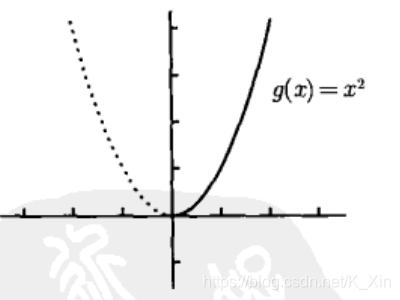
例: F ( x ) = x 2 , x ∈ [ − 2 , 1 ] F(x) = x^2,x ∈ [-2,1] F(x)=x2,x∈[−2,1]
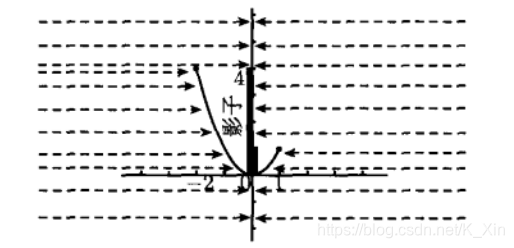
左侧影子的范围是 [ 0 , 4 ] [0,4] [0,4],右侧影子的范围是 [ 0 , 1 ] [0,1] [0,1],值域为并集 [ 0 , 4 ] [0,4] [0,4]
反函数
反函数 f − 1 f^{-1} f−1:如果 f ( x ) = y f(x) = y f(x)=y,那么 f − 1 ( y ) = x f^{-1}(y) = x f−1(y)=x。
(1) f f f 值域的任意 y y y,只有一个 x x x 值满足 f ( x ) = y f(x) = y f(x)=y
(2) f − 1 f^{-1} f−1 的定义域是 f f f 的值域, f − 1 f^{-1} f−1 的值域是 f f f 的定义域
1. 水平线检验反函数
如果每一条水平线和一个函数的图像相交至多一次,那么该函数有一个反函数。
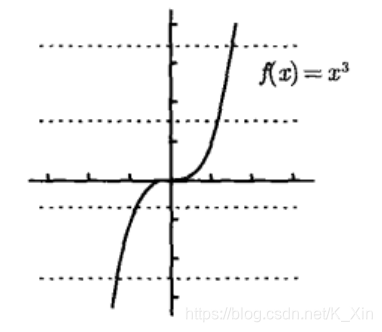
2. 求反函数
(1) 解出 x x x: f ( x ) = x 3 f(x) = x^3 f(x)=x3 即 y = x 3 y = x^3 y=x3,所以 x x x = y 3 \sqrt[3]{y} 3y 即 f − 1 ( y ) = y 3 f^{-1}(y) = \sqrt[3]{y} f−1(y)=3y
(2) 作图 y = x y = x y=x:反函数图像为原函数图像关于 y = x y = x y=x 的镜像。
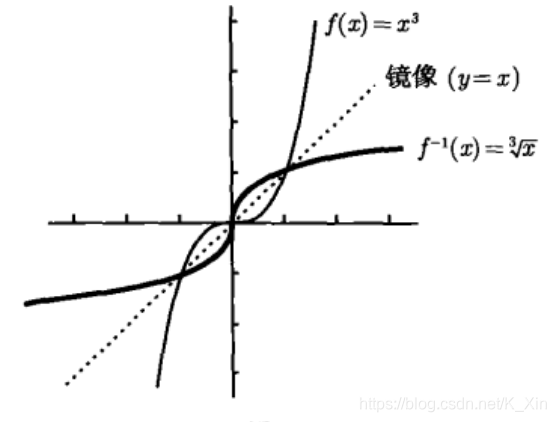
3. 限制定义域
如果水平线检验失败证明没有反函数,可以限制函数的定义域(即删除部分曲线)通过水平线检验。
常见函数及图像
1. 线性函数
(1) 点斜式: y − y 0 = m ( x − x 0 ) y-y_0 = m(x-x_0) y−y0=m(x−x0)
(2) 两点式: y − y 1 = y 2 − y 1 x 2 − x 1 ( x − x 1 ) y-y_1 = \frac{y_2-y_1}{x_2-x_1}(x-x_1) y−y1=x2−x1y2−y1(x−x1)
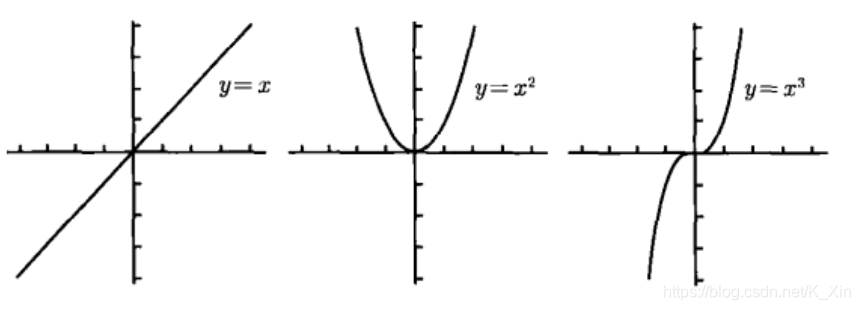
2. 多项式函数
(1) p ( x ) = x n p(x) = x^n p(x)=xn
(2) p ( x ) = a n x n + . . . + a 2 x 2 + a 1 x 1 + a 0 p(x) = a_nx^n+...+a_2x^2+a_1x^1+a_0 p(x)=anxn+...+a2x2+a1x1+a0

二次函数 p ( x ) = a x 2 + b x + c p(x) = ax^2+bx+c p(x)=ax2+bx+c \qquad − b ± − b 2 − 4 a c 2 a \frac{-b±\sqrt{-b^2-4ac}}{2a} 2a−b±−b2−4ac 或 配方
3. 有理函数
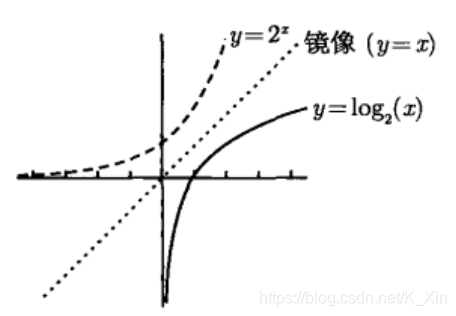
4. 指数函数和对数函数
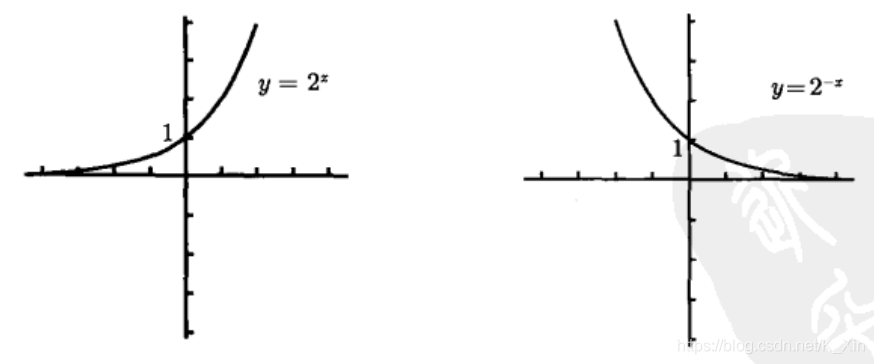
y = 2 x y=2^x y=2x 满足水平线检验,所以反函数 y = l o g 2 ( x ) y=log_2(x) y=log2(x)
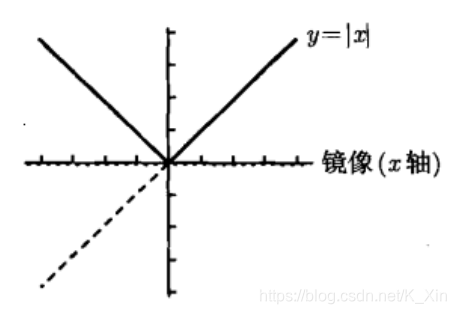
5. 绝对值函数
f ( x ) = ∣ x ∣ = { x x≥0 − x x<0 f(x)=|x|= \begin{cases} x& \text{x≥0}\\ -x& \text{x<0} \end{cases} f(x)=∣x∣={x−xx≥0x<0
函数基本特性
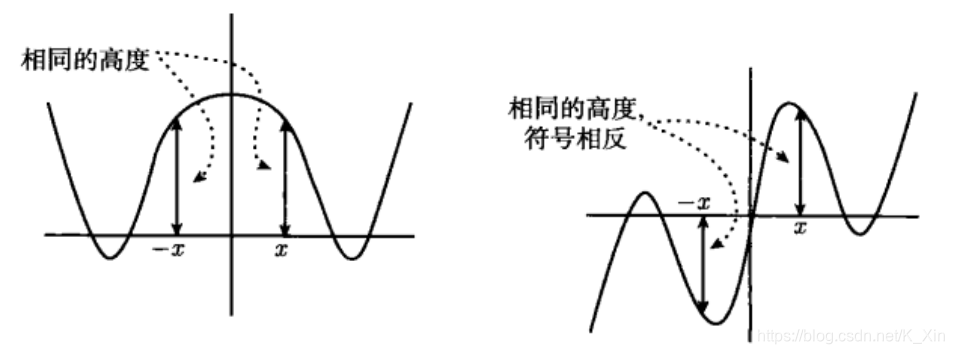
1. 复合、奇函数和偶函数
复合函数: f ( x ) = h ( g ( x ) ) < = > f = h ○ g f(x) = h(g(x)) <=> f = h ○ g f(x)=h(g(x))<=>f=h○g \quad 右移: f ( x − a ) f(x-a) f(x−a) \quad 左移: f ( x + a ) f(x+a) f(x+a)
奇函数: f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x) \quad 关于原点 180 ° 180° 180°点对称 \quad 奇·奇 = 偶 \quad 奇·偶 = 奇
偶函数: f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x) \qquad 关于 y y y 轴镜面对称 \quad 偶·偶 = 偶
2. 单调函数
设函数 f ( x ) f(x) f(x) 的定义域为 D D D, ∀ x 1 , x 2 ∈ D \forall x_1,x_2 ∈ D ∀x1,x2∈D,且 x 1 < x 2 x_1
(1) 若 f ( x 1 ) < f ( x 2 ) f(x_1) < f(x_2) f(x1)<f(x2),则称函数 f ( x ) f(x) f(x) 为区间 D D D 的单调递增函数
(2) 若 f ( x 1 ) > f ( x 2 ) f(x_1) > f(x_2) f(x1)>f(x2),则称函数 f ( x ) f(x) f(x) 为区间 D D D 的单调递减函数
3. 周期函数
设函数 f ( x ) f(x) f(x) 的定义域为 D D D, ∃ ∃ ∃ 正数 T T T, ∀ x ∈ D \forall x∈ D ∀x∈D 与 ( x ± T ) ∈ D (x±T)∈ D (x±T)∈D:
\qquad \qquad \qquad \qquad \quad f ( x + T ) = f ( x ) f(x+T) = f(x) f(x+T)=f(x)
恒成立,则该函数为周期函数,且最小的正数 T T T 为函数 f ( x ) f(x) f(x) 的最小正周期
4. 有界函数
有界:设函数 f ( x ) f(x) f(x) 的定义域为 D D D, ∃ ∃ ∃ 正数 M M M, ∀ x ∈ D \forall x∈ D ∀x∈D,恒有 ∣ f ( x ) ∣ ≤ M |f(x)| ≤ M ∣f(x)∣≤M
无界:设函数有界,取反例证明无界
三角函数
1. 弧度和三角函数

弧 度 = π 180 ∗ 角 度 弧度 = \frac{π}{180} * 角度 弧度=180π∗角度

s i n θ = 对 边 斜 边 c o s θ = 邻 边 斜 边 t a n θ = 对 边 邻 边 sinθ=\frac{对边}{斜边}\qquad cosθ=\frac{邻边}{斜边}\qquad tanθ=\frac{对边}{邻边} sinθ=斜边对边cosθ=斜边邻边tanθ=邻边对边 c s c = 1 s i n θ s e c θ = 1 c o s θ c o t θ = 1 t a n θ csc=\frac{1}{sinθ}\qquad secθ=\frac{1}{cosθ}\qquad cotθ=\frac{1}{tanθ} csc=sinθ1secθ=cosθ1cotθ=tanθ1
2. 三角函数的值
当 x ∈ [ 0 , π / 2 ] x∈ [0,π/2] x∈[0,π/2] 时,
| 0 0 0 | π 6 \frac{π}{6} 6π | π 4 \frac{π}{4} 4π | π 3 \frac{π}{3} 3π | π 2 \frac{π}{2} 2π | |
|---|---|---|---|---|---|
| sin | 0 | 1 2 \frac{1}{2} 21 | 2 2 \frac{\sqrt{2}}{2} 22 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 |
| cos | 1 | 3 2 \frac{\sqrt{3}}{2} 23 | 2 2 \frac{\sqrt{2}}{2} 22 | 1 2 \frac{1}{2} 21 | 0 |
| tan | 0 | 1 3 \frac{1}{\sqrt{3}} 31 | 1 | 3 \sqrt{3} 3 | \ |
当 x ∈ [ 0 , 2 π ] x∈ [0,2π] x∈[0,2π] 时,
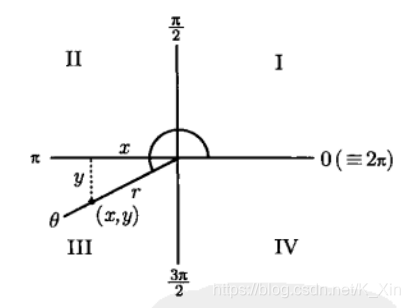
s i n θ = y r c o s θ = x r t a n θ = y x sinθ=\frac{y}{r}\qquad cosθ=\frac{x}{r}\qquad tanθ=\frac{y}{x} sinθ=rycosθ=rxtanθ=xy
画出象限图表,标出角的位置射线及找出射线与 x x x 轴间最小的角,查上表可知该角的三角函数值,最后根据射线所在象限及使用的三角函数决定是否添加符号。
当 x ∉ [ 0 , 2 π ] x∉ [0,2π] x∈/[0,2π] 时,弧度 ± 2 n π ±2nπ ±2nπ 使其限定于 [ 0 , 2 π ] [0,2π] [0,2π] 再计算三角函数值。
3. 三角函数的图像
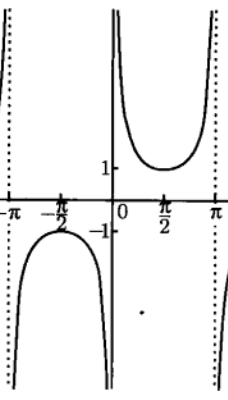
奇 函 数 : y = s i n x y = c s c x 奇函数:y=sinx\qquad y=cscx 奇函数:y=sinxy=cscx
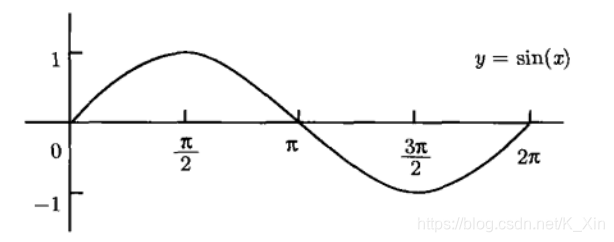
偶 函 数 : y = c o s x y = s e c x 偶函数:y=cosx\qquad y=secx 偶函数:y=cosxy=secx
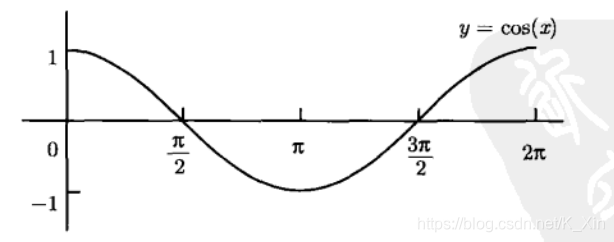
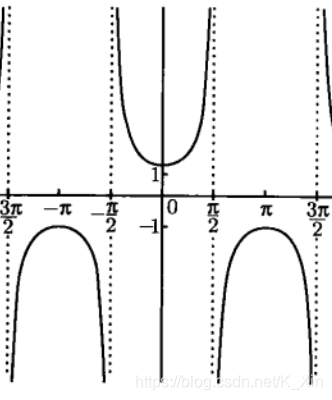
奇 函 数 : y = t a n x y = c o t x 奇函数:y=tanx\qquad y=cotx 奇函数:y=tanxy=cotx

4. 三角恒等式
(1) t a n x = s i n x / c o s x tanx = sinx/cosx tanx=sinx/cosx c o t x = c o s x / s i n x \qquad cotx = cosx/sinx cotx=cosx/sinx
(2) s i n 2 x + c o s 2 x = 1 sin^2x + cos^2x = 1 sin2x+cos2x=1 两 边 同 除 cos 2 x , 1 + t a n 2 x = s e c 2 x \qquad两边同除\cos^2x,1+tan^2x=sec^2x 两边同除cos2x,1+tan2x=sec2x
三角函数 (x) = 互余三角函数(π/2-x)
s i n x = c o s ( π / 2 − x ) sinx = cos(π/2-x) sinx=cos(π/2−x) t a n x = c o t ( π / 2 − x ) \qquad tanx = cot(π/2-x) tanx=cot(π/2−x) s e c x = c s c ( π / 2 − x ) \qquad secx = csc(π/2-x) secx=csc(π/2−x)
求和与倍角公式
(1) sin ( a + b ) = sin ( a ) cos ( b ) + cos ( a ) sin ( b ) \sin(a+b) = \sin(a)\cos(b) + \cos(a)\sin(b) sin(a+b)=sin(a)cos(b)+cos(a)sin(b) sin ( 2 x ) = 2 s i n x c o s x \qquad \sin(2x)=2sinxcosx sin(2x)=2sinxcosx
(2) cos ( a + b ) = cos ( a ) cos ( b ) − sin ( a ) sin ( b ) \cos(a+b) = \cos(a)\cos(b) - \sin(a)\sin(b) cos(a+b)=cos(a)cos(b)−sin(a)sin(b) cos ( 2 x ) = 2 cos 2 x − 1 = 1 − 2 sin 2 x \qquad \cos(2x)=2\cos^2x-1=1-2\sin^2x cos(2x)=2cos2x−1=1−2sin2x
(3) sin 2 x = ( 1 − cos 2 x ) / 2 cos 2 x = ( 1 + cos 2 x ) / 2 \sin ^2x = (1-\cos 2x)/2 \qquad \cos ^2x = (1+\cos 2x)/2 sin2x=(1−cos2x)/2cos2x=(1+cos2x)/2
和差化积:
sin α + sin β = 2 sin α + β 2 cos α − β 2 cos α + cos β = 2 cos α + β 2 cos α − β 2 \sin \alpha+\sin \beta = 2\sin \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} \qquad \cos \alpha+\cos \beta = 2\cos \frac{\alpha+\beta}{2} \cos \frac{\alpha-\beta}{2} sinα+sinβ=2sin2α+βcos2α−βcosα+cosβ=2cos2α+βcos2α−β
积化和差:
- sin α cos β = 1 2 [ sin ( α + β ) + sin ( α − β ) ] \sin \alpha \cos \beta = \frac{1}{2} [\sin(\alpha + \beta) + \sin(\alpha - \beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]
- cos α cos β = 1 2 [ cos ( α + β ) + cos ( α − β ) ] \cos \alpha \cos \beta = \frac{1}{2} [\cos(\alpha + \beta) + \cos(\alpha - \beta)] cosαcosβ=21[cos(α+β)+cos(α−β)]
数列前 n 项和:
- ∑ 1 n k = 1 + 2 + 3 + . . . + n = n ( n + 1 ) 2 \sum_{1}^{n} k=1+2+3+...+n=\frac{n(n+1)}{2} ∑1nk=1+2+3+...+n=2n(n+1)
- ∑ 1 n k 2 = 1 + 2 2 + 3 2 + . . . + n 2 = n ( n + 1 ) 2 ⋅ ( 2 n + 1 ) 3 \sum_{1}^{n} k^2=1+2^2+3^2+...+n^2=\frac{n(n+1)}{2}·\frac{(2n+1)}{3} ∑1nk2=1+22+32+...+n2=2n(n+1)⋅3(2n+1)
- ∑ 1 n k 3 = 1 + 2 3 + 3 3 + . . . + n 3 = n ( n + 1 ) 2 ⋅ n ( n + 1 ) 2 \sum_{1}^{n} k^3=1+2^3+3^3+...+n^3=\frac{n(n+1)}{2}·\frac{n(n+1)}{2} ∑1nk3=1+23+33+...+n3=2n(n+1)⋅2n(n+1)
- ∑ 1 n k ( k + 1 ) = 1 ∗ 2 + 2 ∗ 3 + 3 ∗ 4 + . . . + n ( n + 1 ) = n ( n + 1 ) 2 ⋅ ( 2 n + 4 ) 3 \sum_{1}^{n} k(k+1)=1*2+2*3+3*4+...+n(n+1)=\frac{n(n+1)}{2}·\frac{(2n+4)}{3} ∑1nk(k+1)=1∗2+2∗3+3∗4+...+n(n+1)=2n(n+1)⋅3(2n+4)
- ∑ 1 n 1 k ( k + 1 ) = 1 1 ∗ 2 + 1 2 ∗ 3 + 1 3 ∗ 4 + . . . + 1 n ( n + 1 ) = 1 − 1 n + 1 \sum_{1}^{n} \frac{1}{k(k+1)}=\frac{1}{1*2}+\frac{1}{2*3}+\frac{1}{3*4}+...+\frac{1}{n(n+1)}=1-\frac{1}{n+1} ∑1nk(k+1)1=1∗21+2∗31+3∗41+...+n(n+1)1=1−n+11
阶乘:
- n ! = 1 ∗ 2 ∗ 3 ∗ . . . ∗ n , 规 定 0 ! = 1 n!=1*2*3*...*n,规定 0!=1 n!=1∗2∗3∗...∗n,规定0!=1
- ( 2 n ) ! ! = 2 ∗ 4 ∗ 6 ∗ . . . ∗ ( 2 n ) = 2 n ∗ n ! (2n)!!=2*4*6*...*(2n)=2^n*n! (2n)!!=2∗4∗6∗...∗(2n)=2n∗n!
- ( 2 n + 1 ) ! ! = 1 ∗ 3 ∗ 5 ∗ . . . ∗ ( 2 n − 1 ) (2n+1)!!=1*3*5*...*(2n-1) (2n+1)!!=1∗3∗5∗...∗(2n−1)
因式分解:
- ( a + b ) 3 = a 3 + b 3 + 3 a 2 b + 3 a b 2 (a+b)^3=a^3+b^3+3a^2b+3ab^2 (a+b)3=a3+b3+3a2b+3ab2
- ( a − b ) 3 = a 3 − b 3 − 3 a 2 b + 3 a b 2 (a-b)^3=a^3-b^3-3a^2b+3ab^2 (a−b)3=a3−b3−3a2b+3ab2
- a 3 + b 3 = ( a + b ) ( a 2 − a b + b 2 ) a^3+b^3=(a+b)(a^2-ab+b^2) a3+b3=(a+b)(a2−ab+b2)
- a 3 − b 3 = ( a − b ) ( a 2 + a b + b 2 ) a^3-b^3=(a-b)(a^2+ab+b^2) a3−b3=(a−b)(a2+ab+b2)
二项式定理: ( a + b ) n = ∑ k = 0 n C n k a k b n − k = a n + n a n − 1 b + n ( n − 1 ) 2 ! a n − 2 b 2 + . . . + n a b n − 1 + b n (a+b)^n=\sum_{k=0}^{n}C_n^{k}a^{k} b^{n-k} = a^n +na^{n-1}b+\frac{n(n-1)}{2!}a^{n-2}b^{2}+...+nab^{n-1}+b^n (a+b)n=∑k=0nCnkakbn−k=an+nan−1b+2!n(n−1)an−2b2+...+nabn−1+bn
参考资料
《普林斯顿微积分读本》
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!