卧式储罐不同液位下容积计算（附C语言代码）

说明：

仅适用于标准椭球型封头的卧式储罐

1. 公式推导
2. C语言代码实现

1.公式推导：

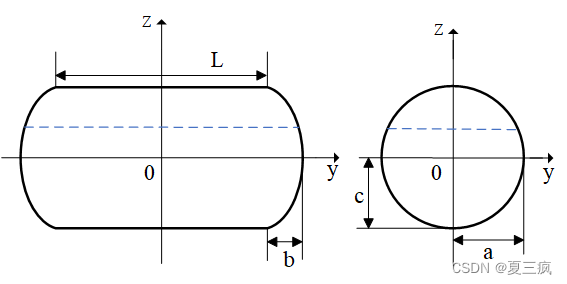
• 封头部分容积计算

椭球方程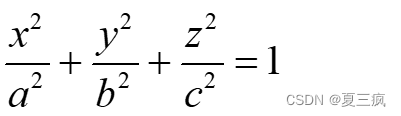：，其中a=c

以面z=z截之，得椭圆面：

与x轴、y轴交点分别为：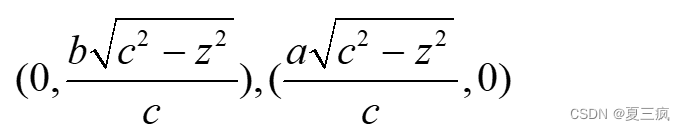

则截面椭圆面积为：​​​​​​​

封头部分液位对应的容积：

• 圆筒体部分容积计算

筒体部分纵断面方程：

水平截面面积：

筒体液位对应的容积：

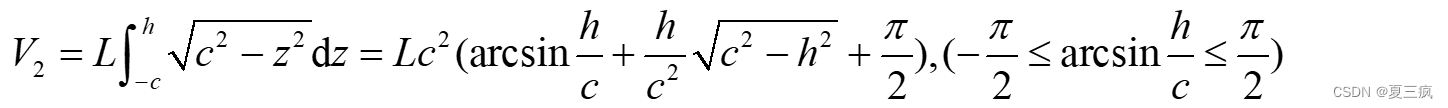
• 卧式储罐不同液面高度下的总容积

2.C语言代码实现：

#include 
#include //单位均为m
//c为圆筒半径，b为椭球封头短半轴长度,h为液位高度(h取值范围是[-c,c],储罐中轴线处h=0),L为储罐圆柱段长度
double waterV(double b, double c, double h, double L)
{double V1, V2, V;double PI = 3.1415926;V1 = PI * b*(c*c*h - pow(h, 3) / 3 + 2 * pow(c, 3) / 3) / c;V2 = L * c*c*(asin(h / c) + h * sqrt(c*c - h * h) / (c*c) + PI / 2);V = V1 + V2;return V;
}int main() 
{printf("液位高度为0.1m（绝对高度为0.925）时对应总容积为：%lf\n", waterV(0.825, 1.65, 0.1, 16.5));//计算示例return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！