时空复杂度（时间复杂度/空间复杂度）O(1)、O(n)、O(n^2)、O(log n)、O(n log n)是什么意思?

时空复杂度（时间复杂度/空间复杂度）O(1)、O(n)、O(n^2)、O(log n)、O(n log n)是什么意思?

能成 架构师小秘圈 今天

大O符号是算法复杂度的相对表示。它描述了时空复杂度.

大O符号是我在大学里学过的东西之一，我了解过这个算法的概念。我知道的不算多，可以回答一些基本的问题，仅此而已。从大学毕业以后，我对这个算法的了解基本没有改变，因为自从我开始工作以来，我没有使用过它，也没有听到任何同事提到过它。所，我想我应该花点时间回顾一下它，并在这篇文章中总结大O符号的基础知识，以及一些代码示例来帮助解释它。

什么是大O符号?简而言之

1. 它是算法复杂度的相对表示。

2. 它描述了一个算法如何执行和缩放。

3. 它描述了函数增长率的上限，可以考虑最坏的情况。

现在快速看一下语法:O(n2)。

n是函数作为输入接收的元素个数。这个例子是说，对于n个输入，它的复杂度等于 n2。

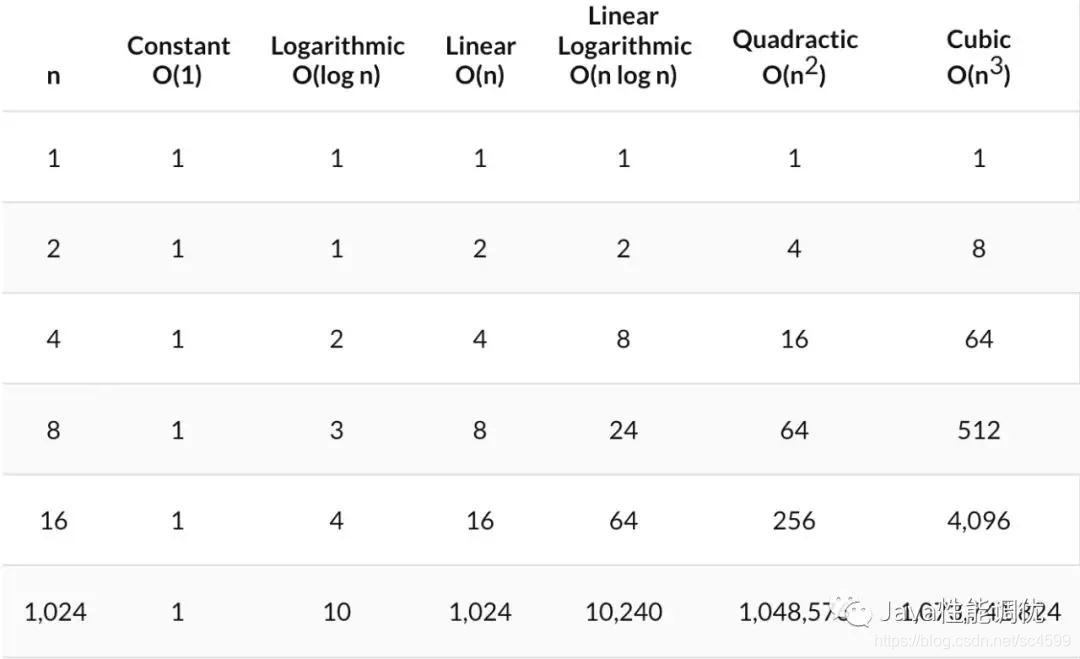
共同复杂性的比较

从这个表中可以看出，随着函数复杂度的增加，完成一个函数所需的计算量或时间可能会显著增加。因此，我们希望将这种增长保持在尽可能低的水平，因为如果函数不能很好地伸缩而增加了输入，可能会出现性能问题。

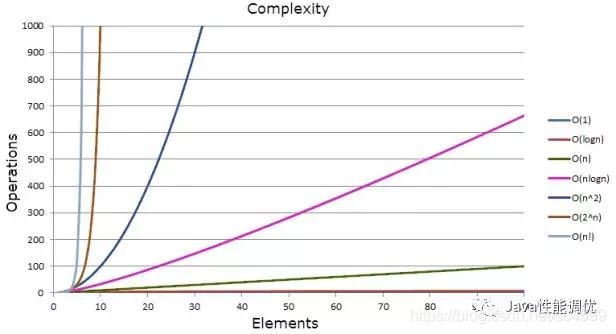
显示操作数量如何随复杂性增加的图表。

一些代码示例应该有助于澄清一些关于复杂性如何影响性能的问题。下面的代码是用python编写的，但是很明显，它可以用其他语言编写。

O(1)

def is_list_first_equal_to_one(data):"""时间复杂度 0(1)检查第一个元素是否为1:param data::return: boole"""return data[0] == 1

O(1) 表示一个函数，无论输入大小如何，该函数总是取相同的值。

O(n)

def contains_num(data, num):"""时间负责度0(n)检查集合是否包含某个元素:param list data: 包含N个元素的list:param int num::return:"""for i in data:if i == num:return Truereturn False

O(n)表示一个函数的复杂度，该函数的复杂度与输入的个数成线性正比增长。这是一个很好的例子，说明大O符号如何描述最坏的情况，因为函数在读取第一个元素后返回true，或者在读取所有n个元素后返回false。

O(n2)

def contains_duplicates(data):"""复杂度O(n2)检查集合中是否有重复元素:param list data: 包含N个元素的list:return:"""for i in range(len(data)):for j in range(len(data)):if i != j and data[i] == data[j]:return Truereturn False

O(n2)  表示一个函数，其复杂度与输入大小的平方成正比。通过输入添加更多的嵌套迭代将增加复杂性，然后可以用3次总迭代表示O(n3)，用4次总迭代表示O(n4) 。

O(n2)

def fibonacci(num):"""O(2n)检查斐波那契数:param num::return:"""if num <= 1:return numelse:return fibonacci(num - 1) + fibonacci(num - 2)

O(2n) 表示一个函数，其性能对输入中的每个元素都加倍。这个例子是斐波那契数列的递归计算。函数属于O(2n)，因为函数对每个输入数递归地调用自身两次，直到该数小于或等于1。

O(log n)

def contains_num_binary_search(data, num):"""O(log n):param list data: 包含N个元素的list:param num::return:"""low = 0high = len(data) - 1while low <= high:middle = low + (high - low)/2if num < data[middle]:hight = middle -1elif num > data[middle]:low = middle + 1else:return Truereturn False

O(log n)表示一个函数，该函数的复杂度随输入大小的增加呈对数增长。这使得O(log n)函数可以很好地伸缩，这样处理较大的输入就不太可能导致性能问题。上面的示例使用二分查找来检查输入列表是否包含某个数字。简单地说，它在每次迭代中将列表一分为二，直到找到数字或读取最后一个元素。此方法具有与O(n)示例相同的功能，尽管实现完全不同且更难于理解。但是，这样做的回报是更大的输入会带来更好的性能(如表中所示)。

这种实现的缺点是二进制搜索依赖于元素已经处于正确的顺序。如果在遍历元素之前需要对元素进行排序，那么这就增加了一些开销。

关于大O符号还有很多内容要讲，但希望你们现在对大O符号的含义有了一个基本的概念以及如何将它转换成你写的代码。如果有必要，大O符号还有后续要讲，若有不懂，欢迎下方留言关注。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！