快速求幂算法 (C实现)

• 今日刷密码学真题时被一道RSA计算题所折磨，结果经过演算发现题目设计本身有谬误。
• 随后本人开始反思自己的做题经历，其中多数都属于数值小而易于破解的题设，因此在这次遇到比较大的数时自乱阵脚，怀疑自己。
• 期间为验证自己的算法出差错与否，于是乎想到回顾参考教材中的快其中一种速幂算法(课后习题中还存在一种实现方式，本文不再实现)，再动手实现它。因此便有了本文。
• 本算法基于C语言实现，从C出发便也可凭借其它语言的基础来实现了。

目录

一、参考样题

二、实现原理

三、代码实现

四、运行与验证

1.运行结果

2.计算器验证

一、参考样题

运用快速求幂算法计算                                                                         

二、实现原理

        模算术里的求幂运算 在 RSA 中，加密和解密都需要计算某整数的模n整数次幂，如果先求出整数的幂，再对n取模，那么中间结果会非常大。幸运的是，正如前面的例子所示，我们可利用模算术的下列性质来计算模幂运算：

        如果重复计算每个中间结果的平方，得到，，和 ，那么只需 4 次乘法即可计算出 x。又比如，对于整数 x 和 n，计算 。由于 ，我们先计算，再计算。

下面我们讨论计算 的算法，如下图所示。表9.4举例说明了该算法的执行过程。请注意，这里的变量c不是必需的，引入它只是为了便于解释算法，c的终值即是指数。 

三、代码实现

• 基于上述的运算原理，将算法步骤以具体源程序编写实现，具体如下：

#include /*变量:1. a —— 底数2. b —— 指数3. n —— 模数4. bit[] —— 存放指数b的二进制形式函数: 1. bits(int) —— 计算指数b的二进制位数，并存储到bit数组2. pow_f(int, int, int) —— 计算带余指数幂
*/int bit[101] = {0};int bits(int b) {int k = 0;while (b) {bit[k] = b & 1;k++;b >>= 1;}return k;
}int pow_f(int a, int b, int n) {int c = 0, f = 1;for (int i = bits(b); i > 0; i--) {c = 2 * c;f = (f * f) % n;if (bit[i - 1] == 1) {c += 1;f = (f * a) % n;}}return f;
}// 主程序测试
int main() {int a, b, n; scanf("%d%d%d", &a, &b, &n);int res = pow_f(a, b, n);printf("%d\n", res);return 0;
}

四、运行与验证

1.运行结果

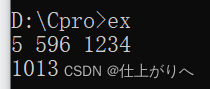
2.计算器验证

每一个不曾起舞的日子，都是对生命的辜负。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！