【Leetcode】括号问题
Leetcode中关于括号问题的汇总,包括有效括号、括号生成、最长有效括号等等。
文章目录
- 面试题 08.09. 括号
- 20. 有效的括号
- 32. 最长有效括号
- 678. 有效的括号字符串
- 921. 使括号有效的最少添加
- 1111. 有效括号的嵌套深度
- 1190. 反转每对括号间的子串
面试题 08.09. 括号
1. 题目描述
leetcode链接:面试题 08.09. 括号

2. 思路分析
回溯法,递归生成括号
- 若右括号的数量大于左括号的数量或者左括号的数量超过n,则终止递归
- 若左括号的数量等于右括号的数量等于n,则添加结果并终止递归
遇到这种需要暴力列举的情况,可以考虑回溯法。
3. 参考代码
class Solution {public List<String> generateParenthesis(int n) {List<String> res = new ArrayList<>();solve(res, "", n, n);return res;}public void solve(List<String> res, String str, int left, int right) {if (left > right || left < 0) {return;}if (left == 0 && right == 0) {res.add(new String(str));return;}solve(res, str + "(", left - 1, right);solve(res, str + ")", left, right - 1);}
}
20. 有效的括号
1. 题目描述
leetcode链接:20. 有效的括号

2. 思路分析
- 遇到左括号,将右括号入栈
- 遇到右括号,判断和出栈的右括号是否相同,或者栈是否空
- 最后返会栈是否空,防止只有左括号
3. 参考代码
class Solution {public boolean isValid(String s) {Deque<Character> stack = new ArrayDeque<>();for (char ch : s.toCharArray()) {if (ch == '(') {stack.push(')');} else if (ch == '['){stack.push(']');} else if (ch == '{') {stack.push('}');} else if (stack.isEmpty() || ch != stack.pop()){return false;}}return stack.isEmpty();}
}
32. 最长有效括号
1. 题目描述
leetcode链接:32. 最长有效括号

2. 思路分析
方法一:栈
使用栈来保存左括号下标,初始化为-1
- 对于左括号,入栈下标
- 对于右括号,出站下标(出栈的左括号对应当前右括号)
- 若栈空,说明不能构成有效括号,入栈当前下标
- 若栈不空,说明出栈下标对应为有效括号,更新最大值
方法二:动态规划
dp[i]表示以第i个元素结尾的最长有效括号的长度
当遇到右括号时,尝试匹配左括号
计算对应左括号的位置,判断左括号是否存在,如果存在则更新匹配长度。
如果是独立的括号对,需要加上该左括号之前对应的括号串长度。
3. 参考代码
方法一:栈
class Solution {public int longestValidParentheses(String s) {Deque<Integer> stack = new ArrayDeque<>();stack.push(-1);int res = 0;for (int i = 0; i < s.length(); i++) {if (s.charAt(i) == '(') {stack.push(i);} else {stack.pop();if (stack.isEmpty()) {stack.push(i);} else {res = Math.max(res, i - stack.peek());}}}return res;}
}
方法二:动态规划
class Solution {public int longestValidParentheses(String s) {int n = s.length();int[] dp = new int[n]; // dp[i]表示以第i个元素结尾的最长有效括号的长度for (int i = 1; i < n; i++) {if (s.charAt(i) == ')') { // 当遇到右括号时,尝试匹配左括号int index = i - dp[i - 1] - 1;if (index >= 0 && s.charAt(index) == '(') { // 如果是左括号,更新匹配长度dp[i] = dp[i - 1] + 2;// 处理独立的括号对if (index > 0) {dp[i] += dp[index - 1];}}}}int res = 0;for (int i = 0; i < dp.length; i++) {res = Math.max(res, dp[i]);}return res;}
}
678. 有效的括号字符串
1. 题目描述
leetcode链接:678. 有效的括号字符串
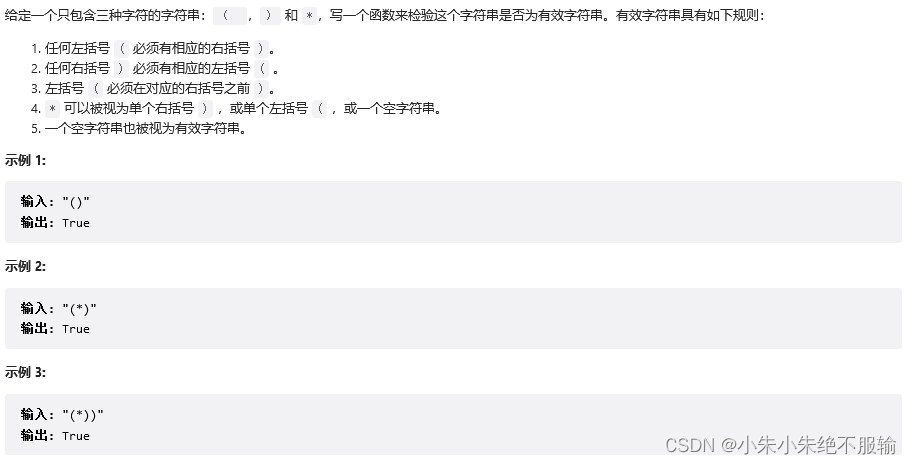
2. 思路分析
方法一:记录当前未匹配左括号数量的范围
这道题是普通括号匹配的变体。回忆一下一般的括号匹配(即没有’*'这个特殊符号),一般用栈来做,栈用来存储左括号,每当遇到右括号时出栈。实际上,这个栈不是必须的,只需要用一个变量记录当前未匹配左括号的数量即可。
从这个角度来看,这道题就会简单很多,加入’*'号后,未匹配左括号的数量从一个值变成了一个范围,所以只需要转变思路,用两个变量来记录这个范围的上下界即可。
方法二:双栈模拟
栈left保存左括号下标,栈star保存*下标,遍历字符串
- 若当前字符为(,则将下标i进栈left
- 若当前字符为*,则将其下标i进栈start
- 若当前字符为),若left不为空,优先配对出栈;若left为空且star不为空,则star出栈(表示当前出栈的下标处*可以表示一个左括号);若left和star均为空,则没有与其配对的,返回false
然后再来看left和star中元素,此时表示*代替右括号来配对left栈中剩余的左括号
- 若left栈顶元素大于star栈顶元素,表示*下标处于左括号下标左边,返回false
- 否则均出栈一个元素,表示配对
最后若left不为空,表示剩余左括号无法配对,返回false,若为空,返回true
3. 参考代码
方法一:记录当前未匹配左括号数量的范围
class Solution {public boolean checkValidString(String s) {// 记录未匹配左括号的上下界int left = 0, right = 0;for (char ch : s.toCharArray()) {if (ch == '(') {left++;right++;} else if (ch == ')') {left = Math.max(0, left - 1);right--;if (right < 0) return false;} else {left = Math.max(0, left - 1);right++;}}return left == 0;}
}
方法二:双栈模拟
class Solution {public boolean checkValidString(String s) {Deque<Integer> left = new ArrayDeque<>();Deque<Integer> star = new ArrayDeque<>();for(int i = 0; i < s.length(); i++) {char c = s.charAt(i);if(c == '(') {left.push(i);}else if(c == '*') {star.push(i);}else {if(!left.isEmpty()) {left.pop();}else if(!star.isEmpty()) {star.pop();}else {return false;}}}while(!left.isEmpty() && !star.isEmpty()) {if(left.pop() > star.pop()) return false;}return left.isEmpty();}
}
921. 使括号有效的最少添加
1. 题目描述
leetcode链接:921. 使括号有效的最少添加
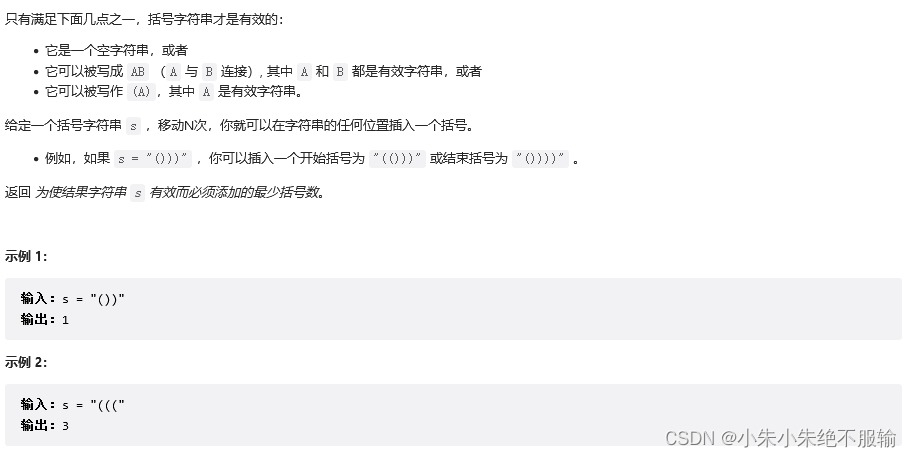
2. 思路分析
方法一:遍历,left标记左括号的个数,add记录添加个数
- 若为左括号,则left++
- 若为右括号,判断left是否为0,如果left大于0,表示当前右括号有匹配的左括号,若left=0,表示没有与之匹配的左括号,则需要添加一个add++。
方法二:字符串替换
使用空字符串替换所有的(),最后剩余字符串的长度就是其未匹配的括号数量
3. 参考代码
方法一:遍历,left标记左括号的个数,add记录添加个数
class Solution {public int minAddToMakeValid(String s) {int left = 0;int add = 0;for (char c : s.toCharArray()) {if (c == '(') {left++;} else {if (left == 0) {add++;} else {left--;}}}return left + add;}
}
方法二:字符串替换
class Solution {public int minAddToMakeValid(String s) {while (s.contains("()")) {s = s.replace("()", "");}return s.length();}
}
1111. 有效括号的嵌套深度
1. 题目描述
leetcode链接:1111. 有效括号的嵌套深度


2. 思路分析
这道题仿佛在考语文。
Seq = ( ( ) ( ( ) ) ( ) )
嵌套深度 = [ 1, 2, 2, 2, 3, 3, 2, 2, 2, 1]
分组情况 = [ A, B, B, B, A, A, B, B, B, A]
输出 = [ 0, 1, 1, 1, 0, 0, 1, 1, 1, 0]
其中把A或B下标的括号单独抽出来,均为合法括号
可见奇数的嵌套深度分配给A,偶数的嵌套深度分配给B
3. 参考代码
class Solution {public int[] maxDepthAfterSplit(String seq) {int[] res = new int[seq.length()];int deep = 0;for (int i = 0; i < seq.length(); i++) {if (seq.charAt(i) == '(') {deep++;res[i] = deep & 1; // 偶数 & 1 = 0,奇数 & 1 = 1} else {res[i] = deep & 1;deep--;}}return res;}
}
1190. 反转每对括号间的子串
1. 题目描述
leetcode链接:1190. 反转每对括号间的子串

2. 思路分析
递归,每匹配一对括号就将对应区间内的字符反转
3. 参考代码
class Solution {public String reverseParentheses(String s) {StringBuilder sb = new StringBuilder();char[] ch = s.toCharArray();Stack<Integer> stack = new Stack<>(); // 栈存下标for (int i = 0; i < ch.length; i++) {if (ch[i] == '(') {stack.push(i);} else if (ch[i] == ')') {reverse(ch, stack.pop() + 1, i - 1);}}for (char c : ch) {if (c != '(' && c != ')') {sb.append(c);}}return sb.toString();}public void reverse(char[] ch, int left, int right) {while (left < right) {char tmp = ch[left];ch[left] = ch[right];ch[right] = tmp;left++;right--;}}
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!