几何求交(二):直线和圆的交点
几何求交:直线和圆的交点
- 1. 向量复习
- 2. 思路解析
- 2.1 总体思路
- 2.2 点在直线上面的投影
- 2.3 点到直线的距离
- 3. 代码解析
- 4. 附录:项目代码
- 5. 参考资料
- 6. 免责声明
1. 向量复习
因为本节需要向量来计算交点,如果大家对向量不是很熟悉,请见:向量复习(一)。已经很熟悉的童鞋,可以跳过这部分内容。
2. 思路解析
2.1 总体思路
如果看过上一节的直线交点,那么这里求直线和圆的交点思路是非常相似的:
- 用直线到圆心的距离和半径相比,判断是否和圆有交点;
- 求出圆心在直线上面的投影点(projectPoint);
- 算出直线的单位向量e;
- 求出一侧交点(Intersection)到projectPoint的长度(sideLength);
- 求出sideLength和这侧端点到projectPoint距离的比例(ratio);
- projectPoint +/- ratio * e = 两侧交点;
同样,我们还是通过一个图例来讲解。我们给定圆,圆心为C,半径为r,和直线AB,以及它们两个交点E和F:
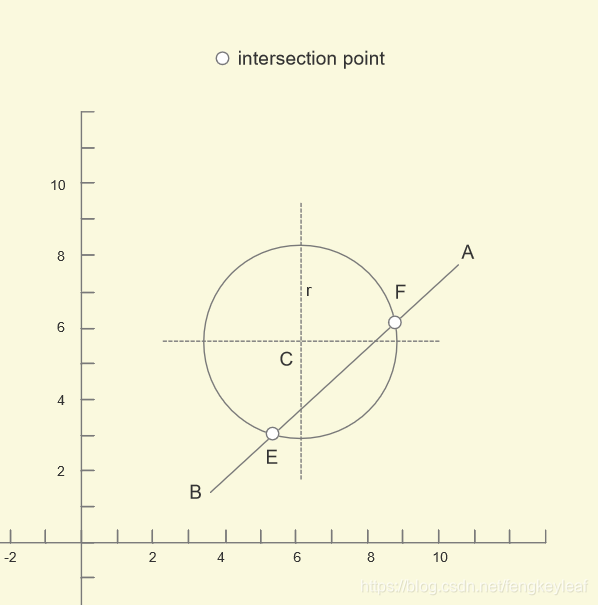
现在我们以求交点E为例来进行讲解。使用求直线交点的思路,如果我们首先会考虑从B出发,求得BE和某个向量的比例,即可通过B来计算交点E,但是这样不是很好找比例,所以我们换一种思路,先求C在直线AB上面的投影Pr:
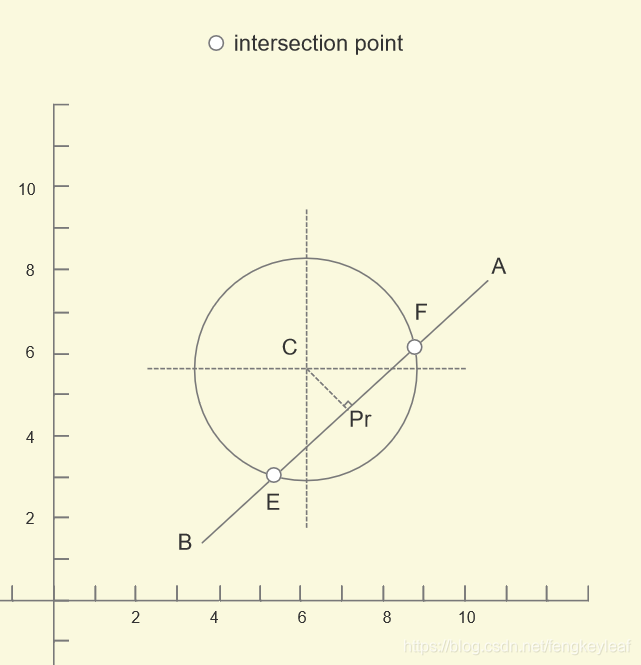
那么显然,我们可以得到一组向量的比例关系:BPr 和 EPr(加粗表示向量),因为圆和直线可能有两个交点,分别位于Pr的两边,所以我们选Pr作为起点求交点比较方便:
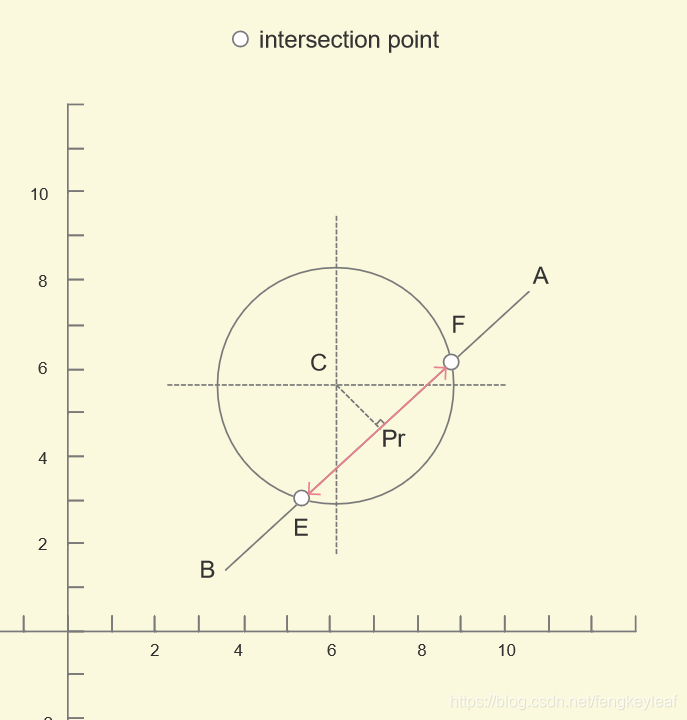
有了这个比例关系(ratio),我们只要知道BA的单位向量e,用 ratio * e,就可以得到EPr和PrF。因为根据垂径定理1,|EPr| = |PrF|。所以我们先假设求得了Pr,那么|EPr|和|BPr|怎么求呢?我们连接BC和EC看看:
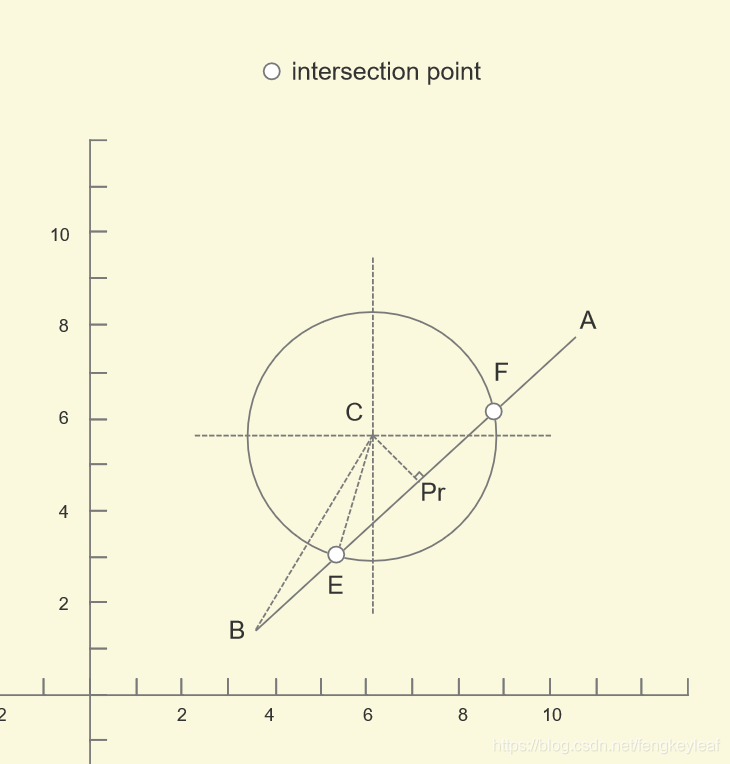
从图中可知,|EPr|不难求,直角三角形CEPr可用勾股定理求得;那么|BPr|呢?现在又需要向量的帮助了,大家还记得向量得点积么?两个向量a和b的点积表示a在b上面的投影,所以|BPr| = BC * BPr。那么到现在,还剩下两个问题就能解决交点了:1)如何求C在直线AB上面的投影;2)如何求C到直线AB的距离;
2.2 点在直线上面的投影
在文章开头,我们曾经提到下面的思路去求解交点:
现在我们以求交点E为例来进行讲解。使用求直线交点的思路,如果我们首先会考虑从B出发,求得BE和某个向量的比例,即可通过B来计算交点E
虽然这个方法求交点不是很好,但是我们可以用它来求解点在直线上面的投影。还是上面圆的图例:

所以我们只需要求出BPr和BA的比例关系,即可以求解Pr,而且|BPr|可以BC和BA的点积来求得,因为两者点积是BC在BA上面的投影,通过这样,我们就能求得比例关系了,如下图所示:

那么,相应的代码也非常容易理解啦哒:
// 这部分是写在Line类里面的:https://github.com/fengkeyleaf/Algorithm/blob/main/ComputationalGeometry/IntersectionOfLineOrCycle/myLibraries/util/geometry/elements/Line.java
/*** get projecting point of the point* */public Vector project( P point ) {Vector base = getVector();float ratio = Vector.dot(point.subtract( startPoint ), base )/ base.normWithoutRadical();return startPoint.add( base.multiply( ratio ) );
}
2.3 点到直线的距离
点到直线的距离,我们可以看成平行四边形的高,然后用叉积来求得,还是刚才的图例:
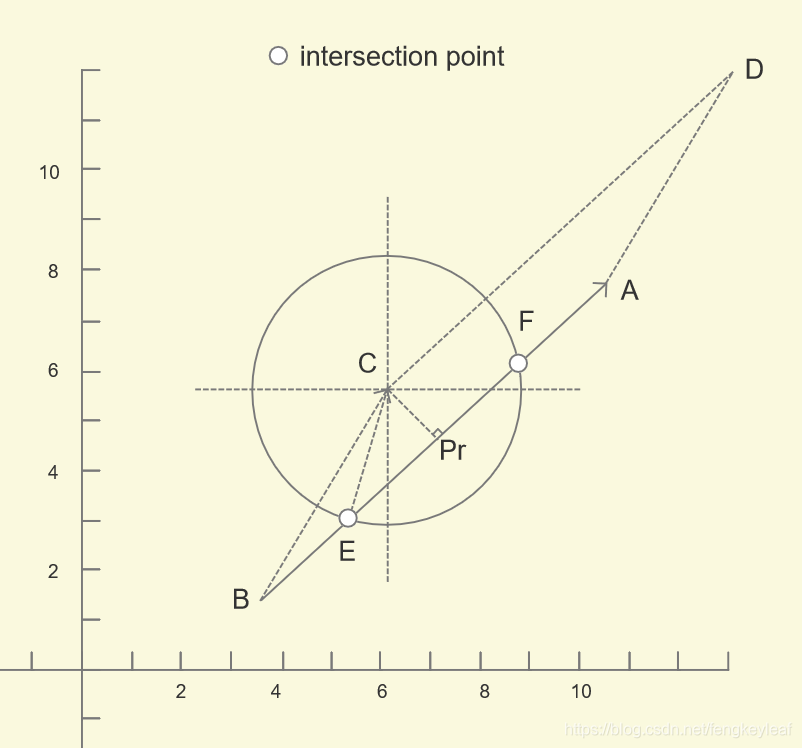
我们看到C到AB的距离(CPr)其实平行四边形BADC的高,所以我们可以利用BC和BA的叉积来求解。
// 详见:https://github.com/fengkeyleaf/Algorithm/blob/main/ComputationalGeometry/IntersectionOfLineOrCycle/myLibraries/util/geometry/elements/Line.java
/*** get the linear distance from the point* */public float distance( P point ) {Vector vector = getVector();float area = Vector.cross( vector, point.subtract( startPoint ) );return Math.abs( area / vector.norm() );
}
3. 代码解析
和直线的交点一样,这里的代码也是上面思路的直接实现:
/*** get the intersection point of line and cycle with vector, if exists** Reference resource:* https://blog.csdn.net/qq_40998706/article/details/87521165*/public static
Line<Vector> lineCycleIntersect( Line<Vector> line, Cycle cycle ) {if ( line == null || cycle == null|| !cycle.ifIntersectsLine( line ) ) return null;Vector projectPoint = line.project( cycle.center );Vector lineVector = line.getVector();Vector e = lineVector.division( lineVector.norm() );float hypotenuse = cycle.radius * cycle.radius -projectPoint.subtract( cycle.center ).normWithoutRadical();float ratio = ( float ) Math.sqrt( Math.abs( hypotenuse ) );Vector distance = e.multiply( ratio );return new Line<>( projectPoint.add( distance ), projectPoint.subtract( distance ) );
}
判断直线和圆是否有交点的方法ifIntersectsLine(),我写在Cycle类里面了:
public class Cycle {public final Vector center;public final float radius;/*** constructs to create an instance of Cycle* */public Cycle( Vector center, float radius ) {this.center = center;this.radius = radius;}/*** intersects with the line?* */public boolean ifIntersectsLine( Line<Vector> line ) {// 避免计算误差return MyMath.doubleCompare( line.distance( center ), radius ) <= 0; }
}
这里的代码和上一节非常的相似,但需要注意一点:
float sideLength = cycle.radius * cycle.radius -projectPoint.subtract( cycle.center ).normWithoutRadical();
float ratio = ( float ) Math.sqrt( Math.abs( sideLength ) );
参考资料里面是这样写的2:
double base = sqrt(c.r * c.r - norm(pr - c.c)); // C++
这里的base就是上面的ratio,开根里面的计算就是计算sideLength,但是这里没有取绝对值,从数学层面来说,这里不需要的,因为我们知道直角三角形的斜边一定是大于等于两个领边的,所以勾股定理算领边不会出现负数的情况,但是代码不是这样的,一旦斜边的平方刚好等于一条领边的平方,因为浮点数计算误差,会出现结果等于负数的情况(非常小的负数,趋近于0),所以为了保险,这里需要取个绝对值,在开根。
这里我们得到一个很重要的代码细节:
以后在开根的时候,即使不取绝对值,也应该assert一下非负,这样如果出现上面的错误,也不会找不到BUG
这个情况的测试案例,大家同样可以在测试代码中找到:
// public static void testLineCycleIntersection()
System.out.println( lineCycleIntersect( line4, cycle ) ); // -11->-1.0002441|0.99975586 -12->-0.99975586|1.0002441
几何求交暂时讲解到这里啦哒,感谢大家看到这里啦,辛苦哒~
上一节:几何求交(一):直线和直线的交点
4. 附录:项目代码
1.1.3 Geometric Intersection
| Description | Entry method\File |
|---|---|
| Line and line | Vector lineIntersect( Line l ) |
| Segment and segment | Vector segmentIntersect( Line l ) |
| Segment and Circle | Vector[] segmentCircle( Segment s, Circle c ) |
| Line and Circle | Line lineCircleIntersect( Line line, Circle circle ) |
| Brute Force | List |
| Bentley Ottmann’s algrithom( Intersection Of segment, ray, line and Circle ) | List |
| Program ( including visualization ) | CG2017 PA1-2 Crossroad |
5. 参考资料
- 计算几何学 | 圆与直线的交点 | Cross Points of a Circle and a Line | C/C++实现
6. 免责声明
※ 本文之中如有错误和不准确的地方,欢迎大家指正哒~
※ 此项目仅用于学习交流,请不要用于任何形式的商用用途,谢谢呢;

垂径定理 ↩︎
计算几何学 | 圆与直线的交点 | Cross Points of a Circle and a Line | C/C++实现 ↩︎
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!