相关系数的概率密度函数分布

相关系数的概率密度函数分布

看了一圈相关系数假设检验的网页，大部分都是t检验z检验什么的，也就是通过构造$\rho$的统计量进行假设检验，有一个大佬推导了更直接的样本相关系数的估计及其分布，然后我也在《高等测量平差》P33页看到了

在文献4中已导出在原假设成立（$\rho =0$）时， ρ ^ \hat \rho ρ^​的密度函数为 f ( ρ ^ ) = Γ ( n − 1 2 ) π Γ ( n − 2 2 ) ( 1 − ρ ^ 2 ) n − 4 2 f\left( {\hat \rho } \right) = {{\Gamma \left( {{{n - 1} \over 2}} \right)} \over {\sqrt \pi \Gamma \left( {{{n - 2} \over 2}} \right)}}{\left( {1 - {{\hat \rho }^2}} \right)^{{{n - 4} \over 2}}} f(ρ^​)=π ​Γ(2n−2​)Γ(2n−1​)​(1−ρ^​2)2n−4​即当$\rho =0$时， ρ ^ \hat \rho ρ^​是具有概率密度为上式的 ρ ^ \hat \rho ρ^​分布统计量，其自由度$f=n-2$。据此，在一定显著性水平$\alpha$下编制了相关系数表，表中自由度$f=n-2$

然后在图书馆里找到了古老的文献4——《概率统计原理和在测量中的应用》，P320页找到了这张表，抄录了下来。

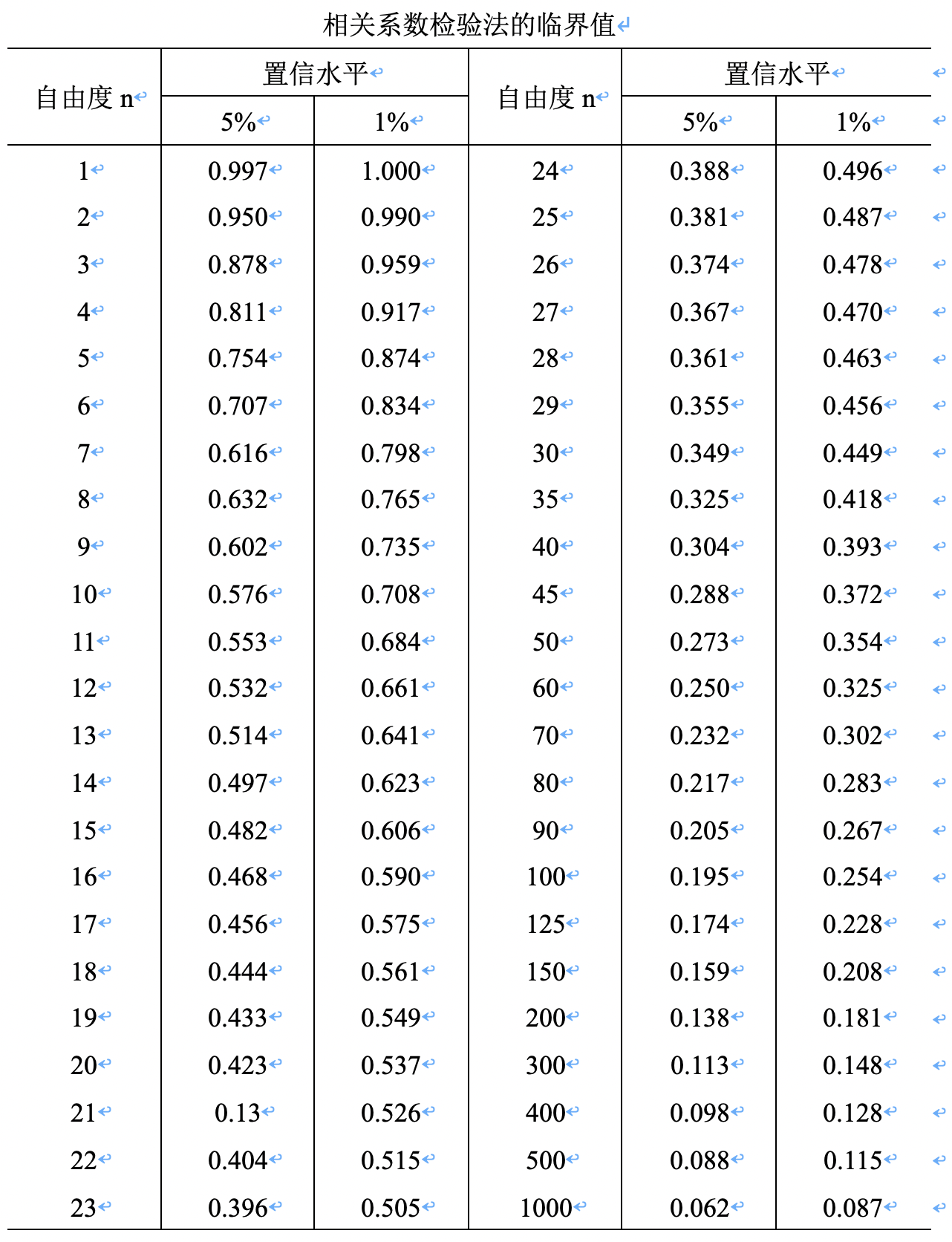
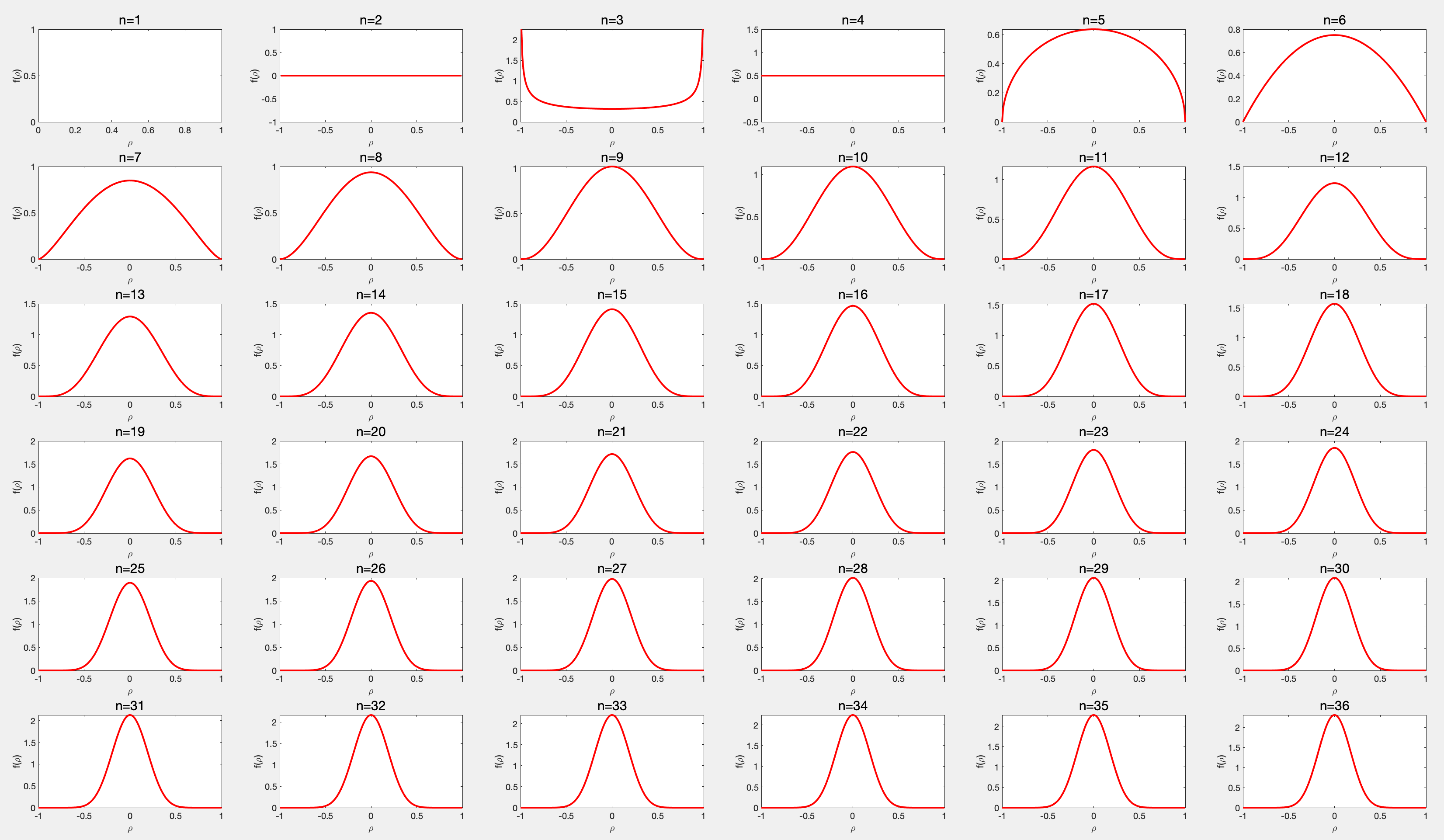
至于概率密度函数的图像大概长这样，$n$较小的时候形状有点奇怪，之后都是变得越来越集中，这也符合常理。值得注意的是利用MATLAB编写的表达式最高只能计算到$n=345$，之后就不收敛了，也不知道老一辈大地测量学家是怎么计算的，竟然能计算到$n=1000$，太强了。

下面是MATLAB画图的代码，很简单看看就好

f=@(n,rho)gamma((n-1)/2)/sqrt(pi)./gamma((n-2)/2).*(1-rho.^2).^((n-4)/2);
rho=-1:0.01:1;
figure;row=6;queue=6;
for i=1:rowfor j=1:queuen=(i-1)*queue+j;subplot(row,queue,n);plot(rho,f(n,rho),'r','linewidth',2);title(sprintf('n=%d',n),'fontsize',15);xlabel('\rho');ylabel('f(\rho)');end
end

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！