leetcode 系列之-DFS题型总结

文章目录

• • • • 一般套路模板
      • 生成匹配的括号85
      • 相同的树 100
      • 组合77
      • 分割回文串
      • 组合总数
      • 组合总数二
      • 子集78
      • 路径总和113
      • 子集二
      • 电话号码的字母组合17
      • 全排列46
      • 戳气球
      • 全排列二
      • 矩阵中的路径jz12
      • 复原ip地址
      • 解数独
      • N 皇后
      • 划分成k个相等的子集698
      • 火柴拼正方形473
      • 未完待续

一般套路模板

DFS 主要用于求解搜索问题和优化问题。 回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

生成匹配的括号85

题目描述

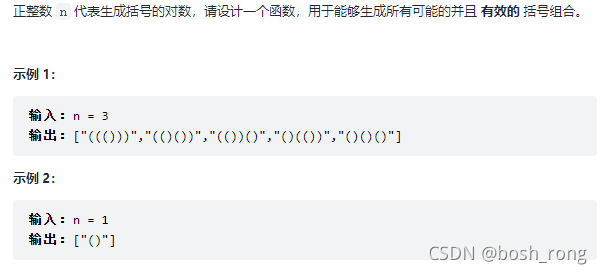
这是一道优化问题，用DFS 去做。创建一颗搜索树。左子树加加左括号，右子树加右括号。但根据实际情况对一些不满足条件的分支进行剪支。

• 1 当前左右括号都有且大于0个可以使用的时候，才会产生分支。
• 2 当产生左分支的时候，只看当前是否还有左括号可以使用。
• 3 产生右分支的时候。还受到左分支的限制，右边剩余可以使用的括号数量一定得严格大于左边剩余的数量的时候，才能产生分支。
• 4 左边和右边剩余的括号数都等于0的时候进行结算。

最终有用的结果，都在搜索数的节点上。

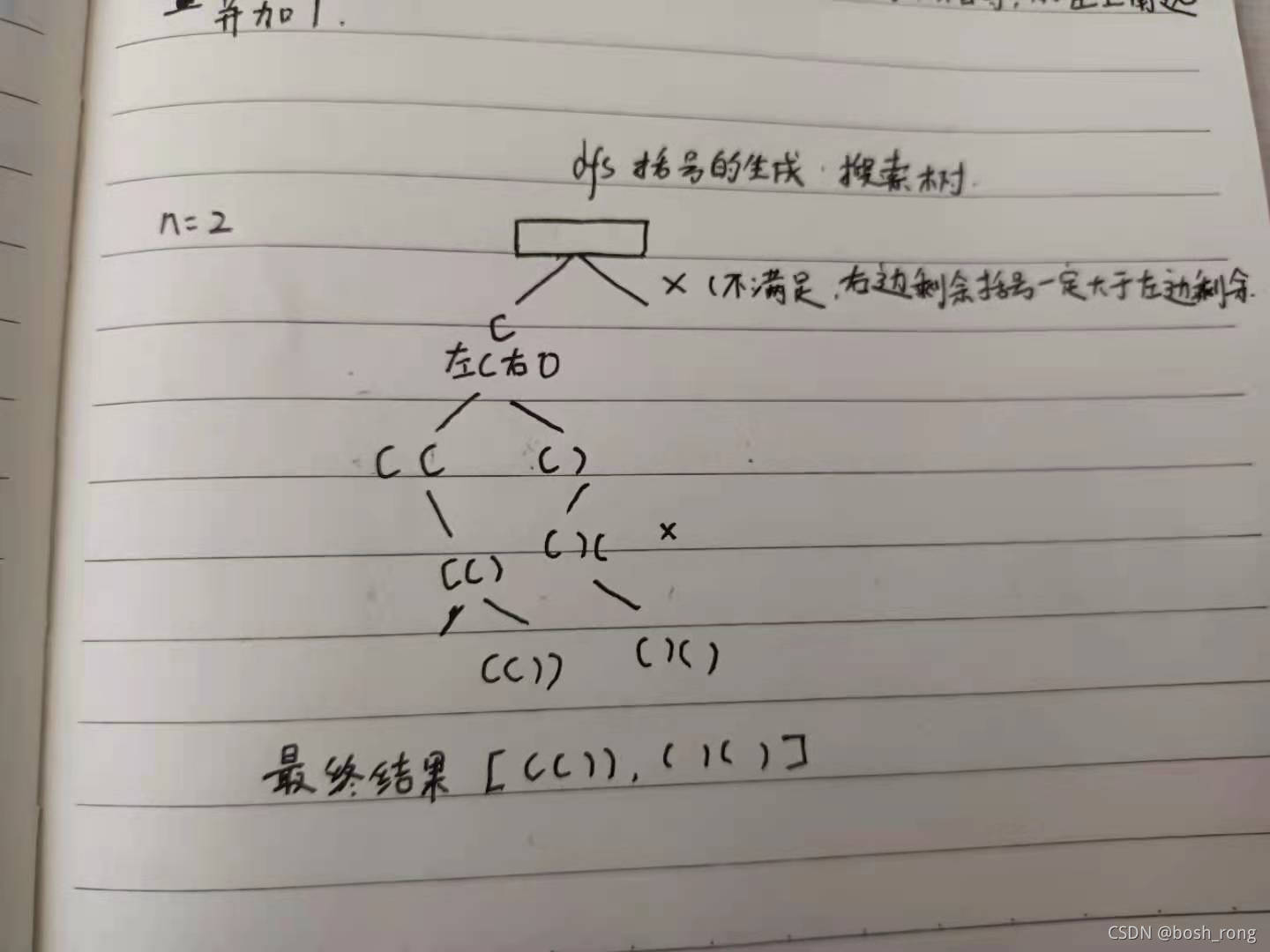
实现
我们需要定义一个string 类型的数组来保存最终的结果。用一个 string 保存当前节点现有的字符串。根据现有状态进行赋值。

代码实现

 static List<String> res;public static List<String> generateParenthesis(int n) {res = new ArrayList<>();dfs(n,n,"");return res;}public static void dfs(int l, int r , String tmp){//到达边界状态进行赋值if(l == 0 && r == 0){res.add(tmp);return;}// 没有出现的时候的递归终止// 右边剩余括号right 要严格大于left. 不满足进行剪支//如果两个中有一个小于0,表示用完了还要用 ，不能产生分支if(l >  r || l < 0 || r < 0) return ;// 每次有两个分支分出去dfs(l-1, r, tmp + '(');dfs(l, r - 1, tmp + ')');}

相同的树 100

题目描述：

要求树有相同的结构和相同的值。用dfs解决。从根结点出发，如果根结点相同 && 根结点的左子树相同 && 根结点的右子树相同，则可以判断两个二叉树相同。

代码实现

public boolean isSameTree(TreeNode p, TreeNode q) {if(p == null && q == null) return true;if(p == null || q == null) return false;if(p.val != q.val ) return false;return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);}

组合77

题目描述：

分析：求所有组合的数，我觉得可以用暴力算法求解，但如歌给的k 值较大其时间复杂度也就会达到O（n^k）。所以暴力解决此问题不是一个很好的选择。这类题也就是常见的回溯组合问题，使用dfs 进行解决。搜索树如下：
分析

• 每一次递归取一个元素，加入到已取元素中。
• 每一次取的元素，要求大于上一次取的元素。( 避免重复)
• 已取元素的个数达到了k, 并满足上述条件将结果进行保存。

代码实现

 public static void dfs(int n,int k,int start,LinkedList<Integer>  tmp,List<List<Integer>> resultList){if(tmp.size()==k){//需要重新赋个值 result 根据tmp 进行变化resultList.add(new ArrayList<>(tmp));return;}for(int i = start;i <= n;i++){tmp.addLast(i);dfs(n,k,i+1,tmp,resultList);tmp.removeLast();}}public static List<List<Integer>> combine(int n, int k) {List<List<Integer>> result = new ArrayList<>();if(n<1||k<1){return result;}// 这里用 双端队列 是自己之前没有考虑到的LinkedList<Integer> queue = new LinkedList<>();dfs(n,k,1,queue,result);return result;}

这里我记录一个问题：如果这里

if(tmp.size()==k){resultList.add(new ArrayList<>(tmp));return;}

赋值的时候没有new ArrayList (tmp) 当返回到上一层递归的时候，tmp就会删除队列最后的元素。进行变动从而改变了resltList的值。最终的结果会返回空。

分割回文串

题目描述

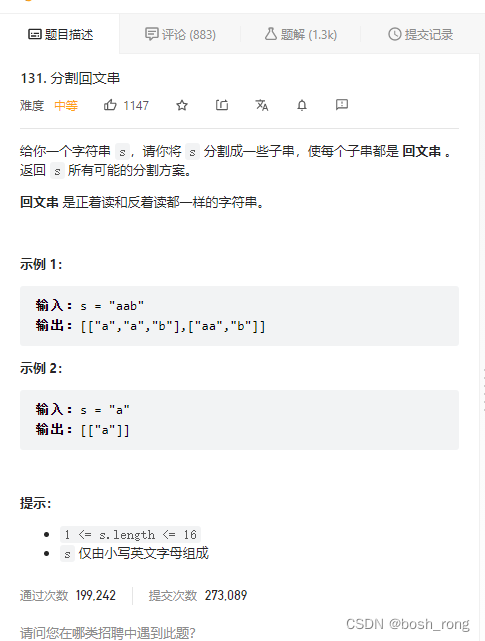
分割回文串本质就是组合问题， 分割的是 每次递归传入到 startIndex 到 i， 每次递归的时候判断是否为回文串，再进行递归。通常要删除最后一个的时候，可以使用双端队列 linkedList 双端队列，调用removeLast() 进行删除。
取一个元素看剩下的是否为回文子串，如果是回文子串将其加入到路径。

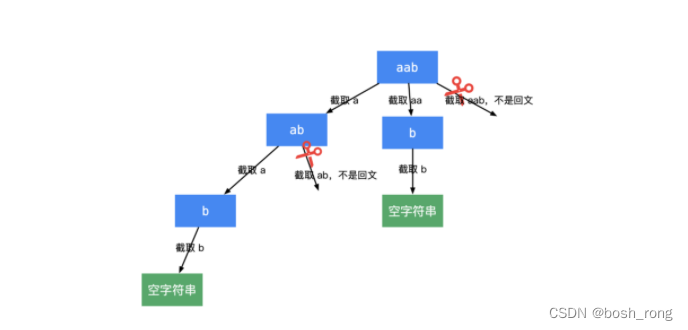
   List<List<String>> res;public List<List<String>> partition(String s) {int n = s.length();this.res = new ArrayList<>();LinkedList<String> path = new LinkedList<>();dfs(s,0,path);return res;}// startIndex 横向， 递归纵向public void dfs(String s, int startIndex, LinkedList<String> path){//结果保存if(startIndex == s.length()){res.add(new ArrayList<>(path));return;}for(int i = startIndex;i < s.length();i++){// statIndex 到i 进行切割if(!isCorrectString(s,startIndex,i)){continue;}// substring 都是小写path.add(s.substring(startIndex,i+1));dfs(s,i+1,path);path.removeLast();}}public boolean isCorrectString(String s,int l, int r){while(l < r && s.charAt(l) == s.charAt(r)){l++;r--;}if(l < r){return false;}return true;}

组合总数

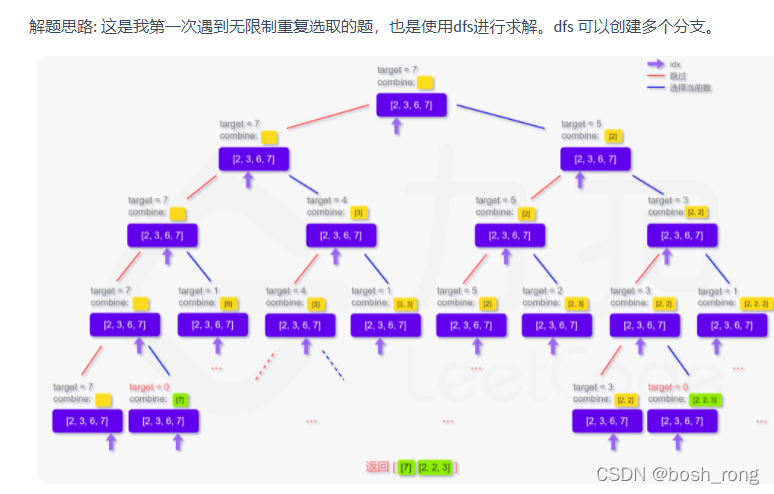
// 主要有个无限重复被选取(无限重复选取可以当做一个进入分支的条件) 只有小于target 的才能被选取 每次dfs 可以选择.
// 怎么也是选与不选的关系public static List<List<Integer>> combinationSum(int[] candidates, int target) {int lens=candidates.length;List<List<Integer>> res=new ArrayList<>();ArrayList<Integer> tmp=new ArrayList();// 通过排序给过了Arrays.sort(candidates);dfs(candidates,tmp,res,0,target);return res;}// 主要有个无限重复被选取(无限重复选取可以当做一个进入分支的条件) 只有小于target 的才能被选取 每次dfs 可以选择.// 怎么也是选与不选的关系 ，选了可能重复选 col 当前在数组的那一位public  static void dfs(int[] candidates,ArrayList<Integer> tmp, List<List<Integer>> res,int col,int target){if(target<0){return;}if(target==0){res.add(new ArrayList<>(tmp));return;}for(int i= col;i <candidates.length; i++){if(target < candidates[i]){return;}       tmp.add(candidates[i]);dfs(candidates,tmp,res,i,target-candidates[i]); // 重复，以i 为开始     tmp.remove(tmp.size()-1);}}

组合总数二

解题思路: 这类题与全排列最大的区别是里面的元素不一定选。保留原有的数组 ,用一个索引指向当前要操作的数。为了去重我先进行了排序，排序后，为了去重使用了set 数据结构。
这里去重的去的是横向的重

添加了一组解，要return

public class 组合总数二 {private int [] candidates;private int target;private List<List<Integer>> res;public List<List<Integer>> combinationSum2(int[] candidates, int target) {this.candidates=candidates;this.target=target;this.res=new ArrayList<>();ArrayList<Integer> path=new ArrayList<>();Arrays.sort(this.candidates);dfs(path,0,0);return res;}public void dfs(ArrayList<Integer> combine,int num,int col){if(col>this.candidates.length){return;}if(num==this.target){this.res.add(new ArrayList<>(combine));return ;}for(int i=col;i<this.candidates.length;i++){if(num+this.candidates[i]>target){break;}combine.add(this.candidates[i]);// 之前写错是因为写成了 col+1dfs(combine,num+this.candidates[i],i+1);combine.remove(combine.size()-1);while(i<this.candidates.length-1 && this.candidates[i]==this.candidates[i+1]){i++;}}}
}

子集78

解题思路: 这与传统的回溯算法不同的时，之前只要收集树的叶子节点，而现在也需要树的非叶节点。每次进入递归前需要保存中间结果。定义一个保存路径和最终结果的数组。进入1 回得到以1开头的所有元素。进入2 之后就不会得到1开头的元素。

List<List<Integer>> res;LinkedList<Integer> path;public List<List<Integer>> subsets(int[] nums) {// 子集 可以采用深搜 分别指向数组的 start end span 每次中的元素个数int lens=nums.length;res=new ArrayList<>();path=new LinkedList<>();if(lens==0){return res;}dfs(nums,0);return res;}public void dfs(int [] nums,int s){res.add(new ArrayList<>(path));if(s>nums.length){return;}for(int i=s;i<nums.length;i++){//如此可以避免重复元素path.add(nums[i]);dfs(nums,i+1);path.removeLast();}}

路径总和113

题目描述：

算法思想： 使用dfs ，并用数组保存过程中的值，每次返回到上一层则进行回溯。
代码实现

public static void dfs(TreeNode root,int targetSum,List<Integer> list,List<List<Integer>> result,int count){if(root==null){return;}count+=root.val;list.add(root.val);if(count==targetSum && root.left==null && root.right==null ){result.add(new ArrayList<>(list));}dfs(root.left,targetSum,list,result,count);dfs(root.right,targetSum,list,result,count);// 返回到上一层递归做的操作int lens=list.size();list.remove(lens-1);count-=root.val;}public static List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<List<Integer>> result = new ArrayList<>();if(root==null){return result;}ArrayList<Integer> list = new ArrayList<>();dfs(root,targetSum,list,result,0);return result;}

子集二

与组合总数二很相似 对于重复元素进行去重， 先进行排序。

 List<List<Integer>> res;LinkedList<Integer> path;public List<List<Integer>> subsetsWithDup(int[] nums) {// 去重，排序去重int lens=nums.length;Arrays.sort(nums);res=new ArrayList<>();path=new LinkedList<>();dfs(nums,0);return res;}public void dfs(int [] nums,int s){res.add(new ArrayList<>(path));if(s>nums.length-1){return;}for(int i=s;i<nums.length;i++){//去重path.add(nums[i]);dfs(nums,i+1);path.removeLast();// 对于重复元素不进行遍历while(i+1<nums.length && nums[i]==nums[i+1]){i++;}}}

电话号码的字母组合17

题目描述

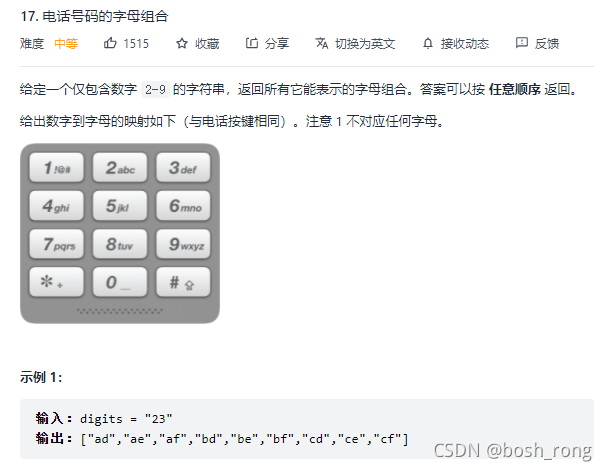
解题思想：使用了 dfs + 数组保存结果。虽然比较慢，但也是自己思索的结果。加油继续努力。

public static void dfs(int begin,String digits,String [] strings,String tempStrings,List<String> result){if(begin==digits.length()){result.add(tempStrings);return;}int i = Integer.parseInt(String.valueOf(digits.charAt(begin)));int length = strings[i-1].length();for (int k=0;k<length;k++){dfs(++begin,digits,strings,tempStrings+strings[i-1].charAt(k),result);begin--;}}public static List<String> letterCombinations(String digits) {//用一个map 存储号码到string的对应关系ArrayList<String > arrayList = new ArrayList<>();int lens=digits.length();if(lens<1){return arrayList;}String [] strings=new String[]{" ","abc","def","ghi","jkl","mno","pqrs","tuv","xwyz"};dfs(0,digits,strings,"",arrayList);return arrayList;}

全排列46

题目描述

解题思路：这道题和电话号码的字母组合比较相似。用dfs 解决，注意在递归中不要更新需要遍历的array 数组的值，如需改变需要开辟新的空间啊。
代码实现

//这道和电话号码那道题比较像// 出问题出在了numspublic static void dfs(List<Integer> nums,List<Integer> list,List<List<Integer>> result){// nums存放剩余的数int lens=nums.size();if(lens==0){result.add(new ArrayList<>(list));return;}for(int i=0;i<lens;i++){list.add(nums.get(i));//新开辟一段空间ArrayList<Integer> arrayList = new ArrayList<>(nums);arrayList.remove(i);dfs(arrayList,list,result);int len=list.size();list.remove(len - 1);}}public static List<List<Integer>> permute(int[] nums) {int lens=nums.length;List<List<Integer>> result = new ArrayList<>();if(lens<1){return result;}ArrayList<Integer> list = new ArrayList<>();ArrayList<Integer> numsArray = new ArrayList<>();for(int i=0;i<lens;i++){numsArray.add(nums[i]);}dfs(numsArray,list,result);return result;}

全排列方法二：
方法二： 使用一个visted 数组，为什么要使用一个visted 数组，因为其i是从0 开始的，之前不用是之前为了避免重复，col= start

public static List<List<Integer>> permute(int[] nums) {int lens=nums.length;List<List<Integer>>  res=new ArrayList<>();if(lens==0){return res;}boolean [] visted= new boolean[lens];ArrayList<Integer> tmp=new ArrayList();dfs(nums,res,tmp,visted);return res;
}public static void dfs(int [] nums,List<List<Integer>>  res,ArrayList<Integer> tmp,boolean [] visted){if(tmp.size()==nums.length){res.add(new ArrayList<>(tmp));return;}for(int i=0;i<nums.length;i++){if(visted[i]==true){continue;}tmp.add(nums[i]);visted[i]=true;dfs(nums,res,tmp,visted);visted[i]=false;tmp.remove(tmp.size()-1);}
}

全排列方法三: 不使用visted 数组

每次使其插入到原来的位置

package com.boshrong.leetcode.dfs;import java.util.ArrayList;
import java.util.List;public class 全排列方法三 {// 这个方法借鉴了戳气球，没有新开辟空间List<List<Integer>> res;public List<List<Integer>> permute(int[] nums) {int lens= nums.length;res=new ArrayList<>();if(lens ==0){return res;}ArrayList<Integer> Arraynum=new ArrayList<>();for(int i=0;i<lens;i++){Arraynum.add(nums[i]);}ArrayList<Integer> tmp=new ArrayList<>();dfs(Arraynum,tmp);return res;}public void dfs(ArrayList<Integer> nums,ArrayList<Integer> tmp){if(nums.size()==0){res.add(new ArrayList<>(tmp));}for(int i=0;i<nums.size();i++){int num=nums.remove(i);tmp.add(num);dfs(nums,tmp);tmp.remove(tmp.size()-1);nums.add(i,num);}}
}

戳气球

题目描述

题解: 戳气球也可以使用回溯去做，代码没有什么问题，但是会超时。用一个值保存当前的最大值，每次更新这个值。

public class 戳气球 {static int ans =0;public int maxCoins(int[] nums) {// 思路: 动态规划，回溯解决ArrayList<Integer> tmp=new ArrayList<>();for(int i=0;i<nums.length;i++){tmp.add(nums[i]);}dfs(tmp,0);return ans;}//tmp 保存现有的值public void dfs(ArrayList<Integer> nums, int tmp){// 递推结束条件,要恢复现场if(nums.size() ==0){ans= Math.max(tmp,ans);return ;}for(int i=0;i<nums.size();i++){//构造结果,放到remove 之前，因为remove 会改变nums.size()int s = nums.get(i) *(i-1<0 ? 1: nums.get(i-1)) * ( i+1>nums.size()-1 ? 1:nums.get(i+1));int num=nums.remove(i);dfs(nums,tmp+s);// 把num 添加到第i 个位置，回溯现场nums.add(i,num);}}
}

全排列二

全排列 一中不包含重复数字，全排列二包含重复数字。全排列二需要对全排列一进行去重。

排序，去重的基础: 将重复元素放在一起，便于找到重复元素和减枝。

求每个

考虑减枝的时候，还要考虑它的重复元素有没有用过。

减枝一: 用过的元素不能在被使用

减枝二: 当当前元素和前一个元素相同，并且元素还没有被使用的使用过的时候进行减枝。

int [] nums;
int lens;
List<List<Integer>> res;
public List<List<Integer>> permuteUnique(int[] nums) {lens=nums.length;res=new ArrayList<>();if(lens==0){return res;}Arrays.sort(nums);this.nums=nums;ArrayList<Integer> tmp=new ArrayList<>();boolean [] visted=new boolean[lens];dfs(tmp,visted);return res;
}
public void dfs(ArrayList<Integer> list,boolean [] visted){if(list.size()==lens){res.add(new ArrayList<>(list));return;}for(int i=0;i<lens;i++){if(visted[i]==true){continue;}if(i>0 && nums[i]==nums[i-1]&&visted[i-1]==false){continue;}list.add(nums[i]);visted[i]=true;dfs(list,visted);visted[i]=false;list.remove(list.size()-1);}}

矩阵中的路径jz12

题目描述

解题思路：解这道题的思路是进行搜索，刚开始找到字符串第一个字符出现的位置。进入dfs,寻找其四周有没有接下来的字符，有则再次进入dfs，没有返回false。
技巧 ： 对于四周可以定义两个数组，分别表示x和y轴。

//定义四个方向 上下左右
static int [] dx=new int[]{-1,0,1,0};
static int [] dy=new int[]{0,1,0,-1};

还有记录一个访问数组，记录被访问的数。

boolean[][] booleans = new boolean[rowlens][clomnlens];

有两次清零，一次是从起始递归出来，一次在遍历四周时，返回false,要将递归进去的访问数组标记为true的设置为false。

代码实现

  //定义四个方向 上下左右static int [] dx=new int[]{-1,0,1,0};static int [] dy=new int[]{0,1,0,-1};static int rowlens;static int clomnlens;static boolean dfs(char [][] matrix,String word,int row,int clomn,int start,boolean[][] booleans){int lens=word.length();if(start==lens){return true;}char s=word.charAt(start);boolean flag=false;//从四周开始找，找到一个合适的字符for(int i=0;i<4;i++){if( 0<=row+dx[i]&& row+dx[i]<rowlens && 0<=clomn+dy[i]&& clomn+dy[i]<clomnlens ){if( booleans[row+dx[i]][clomn+dy[i]]==false){if (matrix[row+dx[i]][clomn+dy[i]]==s){booleans[row+dx[i]][clomn+dy[i]]=true;flag=dfs(matrix,word,row+dx[i],clomn+dy[i],start+1,booleans);if(flag==true){break;}//通过debug 才发现，如果flag为false 将设为true 的置为falsebooleans[row+dx[i]][clomn+dy[i]]=false;}}}}return flag;}public static boolean hasPath (char[][] matrix, String word) {// write code hereint lens=word.length();if(lens<0){return false;}boolean flag=false;rowlens=matrix.length;clomnlens=matrix[0].length;boolean enter= false;//访问矩阵也要传过去,初始全为falseboolean[][] booleans = new boolean[rowlens][clomnlens];for(int i=0;i<rowlens;i++){for(int j=0;j<clomnlens;j++){if (matrix[i][j]==word.charAt(0)){enter=true;booleans[i][j]=true;flag = dfs(matrix, word,i,j, 1,booleans);if(flag==true){break;}}//进入一次递归就要清零if(enter){for (int k=0;k<rowlens;k++){for(int kk=0;kk<clomnlens;kk++){booleans[k][kk]=false;}}enter=false;}}if(flag==true){break;}}return flag;}

运行结果

复原ip地址

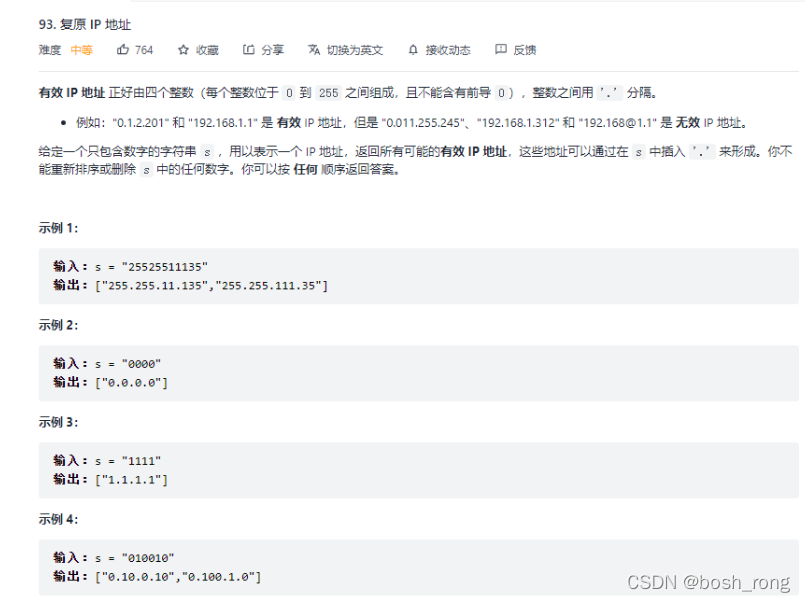
public List<String> restoreIpAddresses(String s) {int len = s.length();List<String> res = new ArrayList<>();// 如果长度不够，不搜索if (len < 4 || len > 12) {return res;}// path 临时存放截取的段Deque<String> path = new ArrayDeque<>(4);int splitTimes = 0;dfs(s, len, splitTimes, 0, path, res);return res;
}//判断截取的段是否满足条件
private int judgeIfIpSegment(String s, int left, int right) {int len = right - left + 1;// 大于 1 位的时候，不能以 0 开头if (len > 1 && s.charAt(left) == '0') {return -1;}// 转成 int 类型int res = 0;for (int i = left; i <= right; i++) {res = res * 10 + s.charAt(i) - '0';}if (res > 255) {return -1;}return res;
}private void dfs(String s, int len, int split, int begin, Deque<String> path, List<String> res) {if (begin == len) {if (split == 4) {res.add(String.join(".", path));}return;}// 看到剩下的不够了，就退出（剪枝），len - begin 表示剩余的还未分割的字符串的位数if (len - begin < (4 - split) || len - begin > 3 * (4 - split)) {return;}for (int i = 0; i < 3; i++) {if (begin + i >= len) {break;}int ipSegment = judgeIfIpSegment(s, begin, begin + i);if (ipSegment != -1) {// 在判断是 ip 段的情况下，才去做截取path.addLast(ipSegment + "");dfs(s, len, split + 1, begin + i + 1, path, res);path.removeLast();}}
}

解数独

解数独本质上是一个搜索的问题，(搜索可以放到其中的数)如果有解进入到下一个分支，且能保障数独关系。如果不能保障回溯现场。回溯就是为了平等对待子节点。

如果 board[i] [j]==‘.’ 搜索可能的数字。
是否有解，根据的是对与给定x, rows[i] 第i 行，是否存在x 这个数， col[i]，第i 列，是否存在x 的这个数。 sub[i/3] [i/3] 是否存在x 这个数。

可以从左往右填，每次遇到列为9，换到下一行，直到行也为9。说明填充结束。

boolean [][] rows= new boolean[9][9];
boolean [][] cols=new boolean[9][9];
boolean [][][] sub=new boolean[3][3][9];
public void solveSudoku(char[][] board) {for(int i=0;i<9;i++){for(int j=0;j<9;j++){if(board[i][j]=='.'){continue;}else{int num=board[i][j]-'1';rows[i][num]=cols[j][num]=sub[i/3][j/3][num]=true;}}}dfs(board,0,0);
}
public boolean dfs(char [][] board,int x,int y){// 从左望右填数字，遇到y=9 越界了if(y==9){x++;y=0;}if(x==9) return true;if(board[x][y]!='.') return dfs(board,x,y+1);for(int i=0;i<9;i++){//判断能否加入if(!cols[x][i] && !rows[y][i] && !sub[x/3][y/3][i]){cols[x][i]=rows[y][i]=sub[x/3][y/3][i]=true;board[x][y]=(char)(i+'1');if(dfs(board,x,y+1)){return true;}//回溯现场board[x][y]='.';cols[x][i]=rows[y][i]=sub[x/3][y/3][i]=false;}}return false;
}

N 皇后

解题思路: 使用回溯算法，每次递归进入一行，遍历这一行的所有列。 判断这一列,只考虑已经排好的，判断45 度对角线和135度对角线可以用两个变量去探索。

   List<List<String>> res;public List<List<String>> solveNQueens(int n) {Character [][] s = new Character[n][n];for(int i = 0; i < n; i++){Arrays.fill(s[i],'.');}res = new ArrayList<>();dfs(n,0,s);return res;}public void dfs(int n, int row, Character [][] s){if(row == n){ArrayList<String> tmp = new ArrayList<>();for(int i = 0; i < n; i++){String t = "";for(int j = 0;j < n;j++){t += s[i][j];}tmp.add(t);}res.add(tmp);return;}// 遍历所有的列for(int col = 0; col < n; col++){if(isValid(s,row,col)){// 满足存放条件s[row][col] = 'Q';dfs(n , row + 1 , s);s[row][col] = '.';}}}public boolean isValid(Character [][] s, int row, int col){// 判断这一列,只考虑已经排好的for(int i = 0; i < row; i++){if(s[i][col] == 'Q'){return false;}}//判断45 度对角线for(int i = row - 1, j = col -1; i >= 0 && j >= 0; i--, j--){if(s[i][j] == 'Q'){return false;}}// 判断135 度对角线for(int i = row - 1, j = col + 1; i >= 0 && j <= s.length -1; i--, j++){if(s[i][j] == 'Q'){return false;}}return true;}

划分成k个相等的子集698

可以使用回溯法，一种思想是桶选择球，第i 层是为 第i 个球做选择。可以放入k个桶。前提是能桶不溢出。终止条件是所有球选择了桶，判断桶的是否等于target ， 如果都相等说明能放入。
每个球能放入则先放入。

public boolean canPartitionKSubsets(int[] nums, int k) {// dfs 终止条件是所有球都放入桶中int n = nums.length;int sum = 0;for(int num : nums){sum += num;}if(sum % k != 0) return false;int target = sum / k;//每个桶必须有元素int [] bucket = new int[k];return dfs(0,nums,bucket, k,target);}public boolean dfs(int s, int [] nums, int [] bucket, int k,int target){if(s == nums.length){for(int i = 0; i < k; i++){if(bucket[i] != target){return false;}}return true;}// 第s 个元素可以选择k个桶，但前提是桶没有溢出for(int i = 0; i < k; i++){if(bucket[i] + nums[s] > target){continue;}bucket[i] += nums[s];if(dfs(s + 1, nums, bucket,k, target)){return true;}bucket[i] -= nums[s];}return false;}

该方法会超时，因为时间复杂度为o（k^n）。
时间复杂度分析:

递归时间复杂度: 递归的次数 * 递归的时间复杂度 就是对应数的节点个数
n层高 的完全二叉树 拥有 2^n -1 个节点, 则时间复杂度为 2的n 次方
n层高的完全k的二叉树拥有 k^n时间复杂度为 k 的n 次方。

时间复杂太高，进行优化。

 // 如果当前桶和上一个桶内的元素和相等，则跳过// 原因：如果元素和相等，那么 nums[index] 选择上一个桶和选择当前桶可以得到的结果是一致的if (i > 0 && bucket[i] == bucket[i - 1]) continue; 

火柴拼正方形473

经典减枝问题:

未完待续

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！