leetCode题型总结

2023-11-23 01:47:27

本文选取了LeetCode和剑指offer中的经典面试题，供大家进行参考

LeetCode

leetcode 总计176道题，下面根据对应目录一一对应。

二分查找
位运算
分治算法
动态规划
双指针
哈希表
图
字符串
排序
搜索
数学
数组+矩阵
栈和队列
树
贪心算法
链表

一、二分查找

* [1. X的平方差](#1-求开方)
* [2. 寻找比目标字母大的最小字母](#2-大于给定元素的最小元素)
* [3. 有序数组中的单一元素](#3-有序数组的-single-element)
* [4. 第一个错误的版本](#4-第一个错误的版本)
* [5. 寻找旋转排序数组中的最小值](#5-旋转数组的最小数字)
* [6.在排序数组中查找元素的第一个和最后一个位置](#6-查找区间)

69.X的平方差

题目：实现 int sqrt(int x) 函数。计算并返回 x 的平方根，其中 x 是非负整数。由于返回类型是整数，结果只保留整数的

部分，小数部分将被舍去。

示例 1: 输入: 4 输出: 2
示例 2: 输入: 8 输出: 2
说明: 8 的平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

解题思路：一个数 x 的开方 sqrt 一定在 0 \~ x 之间，并且满足 sqrt == x / sqrt。可以利用二分查找在 0 \~ x

之间查找 sqrt。对于 x = 8，它的开方是 2.82842...，最后应该返回 2 而不是 3。在循环条件为 l <= h 并且循环退出时，

h 总是比 l 小 1，也就是说 h = 2，l = 3，因此最后的返回值应该为 h 而不是 l。

class Solution {public int mySqrt(int x) {if (x <= 1) {return x;}int l = 1, h = x;while (l <= h) {int mid = l + (h - l) / 2;int sqrt = x / mid;if (sqrt == mid) {return mid;} else if (mid > sqrt) {h = mid - 1;} else {l = mid + 1;}}return h;
}
}

744.寻找比目标字母大的最小字母

给定一个只包含小写字母的有序数组letters 和一个目标字母 target，寻找有序数组里面比目标字母大的最小字母。

数组里字母的顺序是循环的。举个例子，如果目标字母target = 'z' 并且有序数组为 letters = ['a', 'b']，则答案返回 'a'。

示例: 输入: letters = ["c", "f", "j"] target = "a" 输出: "c"

输入: letters = ["c", "f", "j"] target = "c" 输出: "f"

class Solution {public char nextGreatestLetter(char[] letters, char target) {int n = letters.length;int l = 0, h = n - 1;while (l <= h) {int m = l + (h - l) / 2;if (letters[m] <= target) {l = m + 1;} else {h = m - 1;}}return l < n ? letters[l] : letters[0];
}
}

540. 有序数组中的单一元素

给定一个只包含整数的有序数组，每个元素都会出现两次，唯有一个数只会出现一次，找出这个数。

示例 1:输入: [1,1,2,3,3,4,4,8,8] 输出: 2
示例 2:输入: [3,3,7,7,10,11,11] 输出: 10
注意: 您的方案应该在 O(log n)时间复杂度和 O(1)空间复杂度中运行。

class Solution {public int singleNonDuplicate(int[] nums) {int l = 0, h = nums.length - 1;while (l < h) {int m = l + (h - l) / 2;if (m % 2 == 1) {m--;   // 保证 l/h/m 都在偶数位，使得查找区间大小一直都是奇数}if (nums[m] == nums[m + 1]) {l = m + 2;} else {h = m;}}return nums[l];
}
}

278.第一个错误的版本

题目描述：给定一个元素 n 代表有 [1, 2, ..., n] 版本，在第 x 位置开始出现错误版本，导致后面的版本都错误。

可以调用 isBadVersion(int x) 知道某个版本是否错误，要求找到第一个错误的版本。如果第 m 个版本出错，

则表示第一个错误的版本在 [l, m] 之间，令 h = m；否则第一个错误的版本在 [m + 1, h] 之间，令 l = m + 1。

因为 h 的赋值表达式为 h = m，因此循环条件为 l < h。

/* The isBadVersion API is defined in the parent class VersionControl.boolean isBadVersion(int version); */public class Solution extends VersionControl {public int firstBadVersion(int n) {int l = 1, h = n;while (l < h) {int mid = l + (h - l) / 2;if (isBadVersion(mid)) {h = mid;} else {l = mid + 1;}}return l;
}
}

153. 寻找旋转排序数组中的最小值

假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

请找出其中最小的元素。你可以假设数组中不存在重复元素。

示例 1: 输入: [3,4,5,1,2] 输出: 1
示例 2: 输入: [4,5,6,7,0,1,2] 输出: 0

class Solution {public int findMin(int[] nums) {int l = 0, h = nums.length - 1;while (l < h) {int m = l + (h - l) / 2;if (nums[m] <= nums[h]) {h = m;} else {l = m + 1;}}return nums[l];
}
}

34. 在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。你的算法时间复杂度必须是 O(log n) 级别。如果数组中不存在目标值，返回 [-1, -1]。

示例 1: 输入: nums = [5,7,7,8,8,10], target = 8 输出: [3,4]
示例 2: 输入: nums = [5,7,7,8,8,10], target = 6 输出: [-1,-1]

class Solution {public int[] searchRange(int[] nums, int target) {int first = binarySearch(nums, target);int last = binarySearch(nums, target + 1) - 1;if (first == nums.length || nums[first] != target) {return new int[]{-1, -1};} else {return new int[]{first, Math.max(first, last)};}
}private int binarySearch(int[] nums, int target) {int l = 0, h = nums.length; // 注意 h 的初始值while (l < h) {int m = l + (h - l) / 2;if (nums[m] >= target) {h = m;} else {l = m + 1;}}return l;
}
}

二、位运算

* [1. 汉明距离](#1-统计两个数的二进制表示有多少位不同)
* [2. 只出现一次的数字](#2-数组中唯一一个不重复的元素)
* [3. 缺失的数字](#3-找出数组中缺失的那个数)
* [4. 只出现一次的数字 III](#4-数组中不重复的两个元素)
* [5. 颠倒二进制位](#5-翻转一个数的比特位)
* [7. 2的幂](#7-判断一个数是不是-2-的-n-次方)
* [8. 4的幂](#8--判断一个数是不是-4-的-n-次方)
* [9. 交替位二进制数](#9-判断一个数的位级表示是否不会出现连续的-0-和-1)
* [10. 数字的补数](#10-求一个数的补码)
* [11. 两整数之和](#11-实现整数的加法)
* [12. 最大单词长度乘积](#12-字符串数组最大乘积)
* [13. 比特位计数](#13-统计从-0-\~-n-每个数的二进制表示中-1-的个数)

位运算基本概念
**基本原理**
0s 表示一串 0，1s 表示一串 1。
```
x ^ 0s = x x & 0s = 0 x | 0s = x
x ^ 1s = ~x x & 1s = x x | 1s = 1s
x ^ x = 0 x & x = x x | x = x
```
- 利用 x ^ 1s = \~x 的特点，可以将位级表示翻转；利用 x ^ x = 0 的特点，可以将三个数中重复的两个数去除，

只留下另一个数。
- 利用 x & 0s = 0 和 x & 1s = x 的特点，可以实现掩码操作。一个数 num 与 mask：00111100 进行位与操作，

只保留 num 中与 mask 的 1 部分相对应的位。
- 利用 x | 0s = x 和 x | 1s = 1s 的特点，可以实现设值操作。一个数 num 与 mask：00111100 进行位或操作，

将 num 中与 mask 的 1 部分相对应的位都设置为 1。
位与运算技巧：
- n&(n-1) 去除 n 的位级表示中最低的那一位。例如对于二进制表示 10110100，减去 1 得到 10110011，

这两个数相与得到 10110000。
- n&(-n) 得到 n 的位级表示中最低的那一位。-n 得到 n 的反码加 1，对于二进制表示 10110100，-n 得到 01001100，

相与得到 00000100。
- n-n&(\~n+1) 去除 n 的位级表示中最高的那一位。
移位运算：
- \>\> n 为算术右移，相当于除以 2n；
- \>\>\> n 为无符号右移，左边会补上 0。
- << n 为算术左移，相当于乘以 2n。
** mask 计算**
要获取 111111111，将 0 取反即可，\~0。
要得到只有第 i 位为 1 的 mask，将 1 向左移动 i-1 位即可，1<<(i-1) 。例如 1<<4 得到只有第 5 位

为 1 的 mask ：00010000。
要得到 1 到 i 位为 1 的 mask，1<<(i+1)-1 即可，例如将 1<<(4+1)-1 = 00010000-1 = 00001111。
要得到 1 到 i 位为 0 的 mask，只需将 1 到 i 位为 1 的 mask 取反，即 \~(1<<(i+1)-1)。
**Java 中的位操作**
```html
static int Integer.bitCount(); // 统计 1 的数量
static int Integer.highestOneBit(); // 获得最高位
static String toBinaryString(int i); // 转换为二进制表示的字符串

题型如下：

461.汉明距离

class Solution {public int hammingDistance(int x, int y) {int z = x ^ y;int cnt = 0;while(z != 0) {if ((z & 1) == 1) cnt++;z = z >> 1;}return cnt;
}
}

136.只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1: 输入: [2,2,1] 输出: 1
示例 2: 输入: [4,1,2,1,2] 输出: 4

class Solution {public int singleNumber(int[] nums) {int ret = 0;for (int n : nums) ret = ret ^ n;return ret;
}
}

268.缺失的数字

给定一个包含 0, 1, 2, ..., n 中 n 个数的序列，找出 0 .. n 中没有出现在序列中的那个数。

示例 1:输入: [3,0,1] 输出: 2
示例 2: 输入: [9,6,4,2,3,5,7,0,1] 输出: 8

class Solution {public int missingNumber(int[] nums) {int ret = 0;for (int i = 0; i < nums.length; i++) {ret = ret ^ i ^ nums[i];}return ret ^ nums.length;
}
}

260. 只出现一次的数字 III

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。找出只出现一次的那两个元素。

示例 :输入: [1,2,1,3,2,5] 输出: [3,5]

class Solution {public int[] singleNumber(int[] nums) {int diff = 0;for (int num : nums) diff ^= num;diff &= -diff;  // 得到最右一位int[] ret = new int[2];for (int num : nums) {if ((num & diff) == 0) ret[0] ^= num;else ret[1] ^= num;}return ret;
}
}

190.颠倒二进制位

颠倒给定的 32 位无符号整数的二进制位。

public class Solution {// you need treat n as an unsigned valuepublic int reverseBits(int n) {int ret = 0;for (int i = 0; i < 32; i++) {ret <<= 1;ret |= (n & 1);n >>>= 1;}return ret;}
}

231. 2的幂

给定一个整数，编写一个函数来判断它是否是 2 的幂次方。

示例 1: 输入: 1 输出: true 解释: 20 = 1
示例 2: 输入: 16 输出: true 解释: 24 = 16
示例 3: 输入: 218 输出: false

class Solution {public boolean isPowerOfTwo(int n) {return n > 0 && Integer.bitCount(n) == 1;}
}

342. 4的幂

给定一个整数 (32 位有符号整数)，请编写一个函数来判断它是否是 4 的幂次方。

示例 1: 输入: 16 输出: true
示例 2: 输入: 5 输出: false

class Solution {public boolean isPowerOfFour(int num) {return num > 0 && (num & (num - 1)) == 0 && (num & 0b01010101010101010101010101010101) != 0;}
}

693. 交替位二进制数

给定一个正整数，检查他是否为交替位二进制数：换句话说，就是他的二进制数相邻的两个位数永不相等。

示例 1: 输入: 5 输出: True 解释: 5的二进制数是: 101
示例 2: 输入: 7 输出: False 解释: 7的二进制数是: 111
示例 3: 输入: 11 输出: False 解释: 11的二进制数是: 1011

class Solution {public boolean hasAlternatingBits(int n) {int a = (n ^ (n >> 1));return (a & (a + 1)) == 0;
}
}

476. 数字的补数

给定一个正整数，输出它的补数。补数是对该数的二进制表示取反。

注意:给定的整数保证在32位带符号整数的范围内。你可以假定二进制数不包含前导零位。
示例 1: 输入: 5 输出: 2 解释: 5的二进制表示为101（没有前导零位），其补数为010。所以你需要输出2。
示例 2: 输入: 1 输出: 0 解释: 1的二进制表示为1（没有前导零位），其补数为0。所以你需要输出0。

class Solution {public int findComplement(int num) {if (num == 0) return 1;int mask = 1 << 30;while ((num & mask) == 0) mask >>= 1;mask = (mask << 1) - 1;return num ^ mask;}
}

371. 两整数之和

不使用运算符 + 和 - ，计算两整数 a 、b 之和。

示例 1:输入: a = 1, b = 2 输出: 3
示例 2: 输入: a = -2, b = 3 输出: 1

思路：a ^ b 表示没有考虑进位的情况下两数的和，(a & b) << 1 就是进位。递归会终止的原因是 (a & b) << 1 最右边会多一个 0，那么继续递归，进位最右边的 0 会慢慢增多，最后进位会变为 0，递归终止。

class Solution {public int getSum(int a, int b) {return b == 0 ? a : getSum((a ^ b), (a & b) << 1);}
}

318. 最大单词长度乘积

给定一个字符串数组 words，找到 length(word[i]) * length(word[j]) 的最大值，并且这两个单词不含有公共字母。你可以认为每个单词只包含小写字母。如果不存在这样的两个单词，返回 0。

示例 1: 输入: ["abcw","baz","foo","bar","xtfn","abcdef"] 输出: 16 解释: 这两个单词为 "abcw", "xtfn"。
示例 2: 输入: ["a","ab","abc","d","cd","bcd","abcd"] 输出: 4 解释: 这两个单词为 "ab", "cd"。
示例 3: 输入: ["a","aa","aaa","aaaa"] 输出: 0 解释: 不存在这样的两个单词。

class Solution {public int maxProduct(String[] words) {int n = words.length;int[] val = new int[n];for (int i = 0; i < n; i++) {for (char c : words[i].toCharArray()) {val[i] |= 1 << (c - 'a');}}int ret = 0;for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {if ((val[i] & val[j]) == 0) {ret = Math.max(ret, words[i].length() * words[j].length());}}}return ret;}
}

338. 比特位计数

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例 1:输入: 2 输出: [0,1,1]
示例 2: 输入: 5 输出: [0,1,1,2,1,2]

解题思路：对于数字 6(110)，它可以看成是 4(100) 再加一个 2(10)，因此 dp[i] = dp[i&(i-1)] + 1;

class Solution {public int[] countBits(int num) {int[] ret = new int[num + 1];for(int i = 1; i <= num; i++){ret[i] = ret[i&(i-1)] + 1;}return ret;}
}

三、分治算法

* [1. 为运算表达式设计优先级](#1-给表达式加括号)
* [2. 不同的二叉搜索树 II](#2-不同的二叉搜索树)

241. 为运算表达式设计优先级

给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能

的组合的结果。有效的运算符号包含 +, - 以及 * 。

示例 1: 输入: "2-1-1" 输出: [0, 2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2
示例 2: 输入: "2*3-4*5" 输出: [-34, -14, -10, -10, 10]
解释:
(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10

class Solution {public List diffWaysToCompute(String input) {List ways = new ArrayList<>();for (int i = 0; i < input.length(); i++) {char c = input.charAt(i);if (c == '+' || c == '-' || c == '*') {List left = diffWaysToCompute(input.substring(0, i));List right = diffWaysToCompute(input.substring(i + 1));for (int l : left) {for (int r : right) {switch (c) {case '+':ways.add(l + r);break;case '-':ways.add(l - r);break;case '*':ways.add(l * r);break;}}}}}if (ways.size() == 0) {ways.add(Integer.valueOf(input));}return ways;}
}

95. 不同的二叉搜索树 II

给定一个整数 n，生成所有由 1 ... n 为节点所组成的二叉搜索树。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode(int x) { val = x; }* }*/
class Solution {public List generateTrees(int n) {if (n < 1) {return new LinkedList();}return generateSubtrees(1, n);
}private List generateSubtrees(int s, int e) {List res = new LinkedList();if (s > e) {res.add(null);return res;}for (int i = s; i <= e; ++i) {List leftSubtrees = generateSubtrees(s, i - 1);List rightSubtrees = generateSubtrees(i + 1, e);for (TreeNode left : leftSubtrees) {for (TreeNode right : rightSubtrees) {TreeNode root = new TreeNode(i);root.left = left;root.right = right;res.add(root);}}}return res;
}
}

四、动态规划问题

* [斐波那契数列](#斐波那契数列)* [70. 爬楼梯](#1-爬楼梯)* [198. 打家劫舍](#2-强盗抢劫)* [213. 打家劫舍2](#3-强盗在环形街区抢劫)
* [矩阵路径](#矩阵路径)* [64. 最小路径和](#1-矩阵的最小路径和)* [62. 不同路径](#2-矩阵的总路径数)
* [数组区间](#数组区间)* [303. 区域和检索 - 数组不可变](#1-数组区间和)* [413.等差数列划分](#2-数组中等差递增子区间的个数)
* [分割整数](#分割整数)* [343.整数拆分](#1-分割整数的最大乘积)* [279. 完全平方数](#2-按平方数来分割整数)* [91.解码方法](#3-分割整数构成字母字符串)
* [最长递增子序列](#最长递增子序列)* [300 最长上升子序列](#1-最长递增子序列)* [646. 最长数队列](#2-一组整数对能够构成的最长链)* [376.摆动序列](#3-最长摆动子序列)
* [最长公共子序列](#最长公共子序列)
* [0-1 背包](#0-1-背包)* [416.分割等和子集](#1-划分数组为和相等的两部分)* [494.目标和](#2-改变一组数的正负号使得它们的和为一给定数)* [474.一和零](#3-01-字符构成最多的字符串)* [322.零钱兑换](#4-找零钱的最少硬币数)* [518 零钱兑换2](#5-找零钱的硬币数组合)* [139.单词拆分](#6-字符串按单词列表分割)* [377 组合总和IV](#7-组合总和)
* [股票交易](#股票交易)* [309.最佳买卖股票时机含冷冻期](#1-需要冷却期的股票交易)* [714. 买卖股票的最佳时机含手续费](#2-需要交易费用的股票交易)* [123. 买卖股票的最佳时机 III](#3-只能进行两次的股票交易)* [188. 买卖股票的最佳时机 IV](#4-只能进行-k-次的股票交易)
* [字符串编辑](#字符串编辑)* [583. 两个字符串的删除操作](#1-删除两个字符串的字符使它们相等)* [72. 编辑距离](#2-编辑距离)* [650. 只有两个键的键盘](#3-复制粘贴字符)

70. 爬楼梯

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：输入： 2 输出： 2 解释：有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2：输入： 3 输出： 3解释：有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶 3. 2 阶 + 1 阶

class Solution {public int climbStairs(int n) {if (n <= 2) {return n;}int pre2 = 1, pre1 = 2;for (int i = 2; i < n; i++) {int cur = pre1 + pre2;pre2 = pre1;pre1 = cur;}return pre1;}
}

198.打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1: 输入: [1,2,3,1] 输出: 4 解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2: 输入: [2,7,9,3,1] 输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

class Solution {public int rob(int[] nums) {int pre2 = 0, pre1 = 0;for (int i = 0; i < nums.length; i++) {int cur = Math.max(pre2 + nums[i], pre1);pre2 = pre1;pre1 = cur;}return pre1;}
}

213. 打家劫舍2

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈，这意味着第

一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一

晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int n = nums.length;if (n == 1) {return nums[0];}return Math.max(rob(nums, 0, n - 2), rob(nums, 1, n - 1));}private int rob(int[] nums, int first, int last) {int pre2 = 0, pre1 = 0;for (int i = first; i <= last; i++) {int cur = Math.max(pre1, pre2 + nums[i]);pre2 = pre1;pre1 = cur;}return pre1;}
}

# 矩阵路径

64. 最小路径和

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

输入:
[[1,3,1],[1,5,1],[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

class Solution {public int minPathSum(int[][] grid) {if (grid.length == 0 || grid[0].length == 0) {return 0;}int m = grid.length, n = grid[0].length;int[] dp = new int[n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (j == 0) {dp[j] = dp[j];        // 只能从上侧走到该位置} else if (i == 0) {dp[j] = dp[j - 1];    // 只能从左侧走到该位置} else {dp[j] = Math.min(dp[j - 1], dp[j]);}dp[j] += grid[i][j];}}return dp[n - 1];
}
}

62. 不同路径

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。机器人每次只能向下或者向

右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？

class Solution {public int uniquePaths(int m, int n) {int[] dp = new int[n];Arrays.fill(dp, 1);for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[j] = dp[j] + dp[j - 1];}}return dp[n - 1];
}
}

数组区间

303. 区域和检索 - 数组不可变

class NumArray {private int[] sums;public NumArray(int[] nums) {sums = new int[nums.length + 1];for (int i = 1; i <= nums.length; i++) {sums[i] = sums[i - 1] + nums[i - 1];}}public int sumRange(int i, int j) {return sums[j + 1] - sums[i];}
}

413.等差数列划分

如果一个数列至少有三个元素，并且任意两个相邻元素之差相同，则称该数列为等差数列。

数组 A 包含 N 个数，且索引从0开始。数组 A 的一个子数组划分为数组 (P, Q)，P 与 Q 是整数且满足 0<=P

如果满足以下条件，则称子数组(P, Q)为等差数组：

元素 A[P], A[p + 1], ..., A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。

函数要返回数组 A 中所有为等差数组的子数组个数。

class Solution {public int numberOfArithmeticSlices(int[] A) {if (A == null || A.length == 0) {return 0;}int n = A.length;int[] dp = new int[n];for (int i = 2; i < n; i++) {if (A[i] - A[i - 1] == A[i - 1] - A[i - 2]) {dp[i] = dp[i - 1] + 1;}}int total = 0;for (int cnt : dp) {total += cnt;}return total;}
}

# 分割整数

343.整数拆分

给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。返回你可以获得的最大乘积。

示例 1: 输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2: 输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

class Solution {public int integerBreak(int n) {int[] dp = new int[n + 1];dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 1; j <= i - 1; j++) {dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));}}return dp[n];}
}

279. 完全平方数

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全

平方数的个数最少。

示例 1: 输入: n = 12 输出: 3 解释: 12 = 4 + 4 + 4.
示例 2: 输入: n = 13 输出: 2 解释: 13 = 4 + 9.

class Solution {public int numSquares(int n) {List squareList = generateSquareList(n);int[] dp = new int[n + 1];for (int i = 1; i <= n; i++) {int min = Integer.MAX_VALUE;for (int square : squareList) {if (square > i) {break;}min = Math.min(min, dp[i - square] + 1);}dp[i] = min;}return dp[n];}private List generateSquareList(int n) {List squareList = new ArrayList<>();int diff = 3;int square = 1;while (square <= n) {squareList.add(square);square += diff;diff += 2;}return squareList;}
}

91.解码方法

一条包含字母 A-Z 的消息通过以下方式进行了编码：

'A' -> 1
'B' -> 2
...
'Z' -> 26
给定一个只包含数字的非空字符串，请计算解码方法的总数。
示例 1: 输入: "12"  输出: 2  解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。
示例 2: 输入: "226" 输出: 3  解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6)

class Solution {public int numDecodings(String s) {if (s == null || s.length() == 0) {return 0;}int n = s.length();int[] dp = new int[n + 1];dp[0] = 1;dp[1] = s.charAt(0) == '0' ? 0 : 1;for (int i = 2; i <= n; i++) {int one = Integer.valueOf(s.substring(i - 1, i));if (one != 0) {dp[i] += dp[i - 1];}if (s.charAt(i - 2) == '0') {continue;}int two = Integer.valueOf(s.substring(i - 2, i));if (two <= 26) {dp[i] += dp[i - 2];}}return dp[n];
}
}

# 最长递增子序列

300 最长上升子序列

给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例: 输入: [10,9,2,5,3,7,101,18] 输出: 4 解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

class Solution {public int lengthOfLIS(int[] nums) {int n = nums.length;int[] tails = new int[n];int len = 0;for (int num : nums) {int index = binarySearch(tails, len, num);tails[index] = num;if (index == len) {len++;}}return len;}private int binarySearch(int[] tails, int len, int key) {int l = 0, h = len;while (l < h) {int mid = l + (h - l) / 2;if (tails[mid] == key) {return mid;} else if (tails[mid] > key) {h = mid;} else {l = mid + 1;}}return l;}
}

646. 最长数队列

给出 n 个数对。在每一个数对中，第一个数字总是比第二个数字小。现在，我们定义一种跟随关系，

当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。给定一个对数集合，

找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例 : 输入: [[1,2], [2,3], [3,4]] 输出: 2 解释: 最长的数对链是 [1,2] -> [3,4]

class Solution {public int findLongestChain(int[][] pairs) {Arrays.sort(pairs,(a,b)-> a[1]-b[1]);int res = 1,tmp = pairs[0][1];for(int i = 1;i < pairs.length;i++){if(pairs[i][0] > tmp){res++;tmp = pairs[i][1];}}return res;}
}

376.摆动序列

class Solution {public int wiggleMaxLength(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int up = 1, down = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i - 1]) {up = down + 1;} else if (nums[i] < nums[i - 1]) {down = up + 1;}}return Math.max(up, down);}
}

# 最长公共子序列、

对于两个子序列 S1 和 S2，找出它们最长的公共子序列。定义一个二维数组 dp 用来存储最长公共子序列的长度，其中 dp[i][j] 表示 S1 的前 i 个字符与 S2 的前 j

个字符最长公共子序列的长度。考虑 S1i 与 S2j 值是否相等，分为两种情况：

与最长递增子序列相比，最长公共子序列有以下不同点： - 针对的是两个序列，求它们的最长公共子序列。 - 在最长递增子序列中，dp[i] 表示以 Si 为结尾的最长递增子序列长度，

子序列必须包含 Si ；在最长公共子序列中，dp[i][j] 表示 S1 中前 i 个字符与 S2 中前 j 个字符的最长公共子序列长度，

不一定包含 S1i 和 S2j。 - 在求最终解时，最长公共子序列中 dp[N][M] 就是最终解，而最长递增子序列中 dp[N] 不是最终解，

因为以 SN 为结尾的最长递增子序列不一定是整个序列最长递增子序列，需要遍历一遍 dp 数组找到最大者。

public int lengthOfLCS(int[] nums1, int[] nums2) {int n1 = nums1.length, n2 = nums2.length;int[][] dp = new int[n1 + 1][n2 + 1];for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {if (nums1[i - 1] == nums2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);}}}return dp[n1][n2];
}

# 0-1 背包
有一个容量为 N 的背包，要用这个背包装下物品的价值最大，这些物品有两个属性：体积 w 和价值 v。定义一个二维数组 dp 存储最大价值，其中 dp[i][j] 表示前 i 件物品体积不超过 j 的情况下能达到的最大价值。设第 i件物品体积为 w，价值为 v，根据第 i 件物品是否添加到背包中，可以分两种情况讨论：
- 第 i 件物品没添加到背包，总体积不超过 j 的前 i 件物品的最大价值就是总体积不超过 j 的前 i-1 件物品的最大价值，
dp[i][j] = dp[i-1][j]。
- 第 i 件物品添加到背包中，dp[i][j] = dp[i-1][j-w] + v。
第 i 件物品可添加也可以不添加，取决于哪种情况下最大价值更大。因此，0-1 背包的状态转移方程为:

public int knapsack(int W, int N, int[] weights, int[] values) {int[][] dp = new int[N + 1][W + 1];for (int i = 1; i <= N; i++) {int w = weights[i - 1], v = values[i - 1];for (int j = 1; j <= W; j++) {if (j >= w) {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - w] + v);} else {dp[i][j] = dp[i - 1][j];}}}return dp[N][W];
}

416.分割等和子集

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:每个数组中的元素不会超过 100数组的大小不会超过 200
示例 1:输入: [1, 5, 11, 5] 输出: true 解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2: 输入: [1, 2, 3, 5] 输出: false 解释: 数组不能分割成两个元素和相等的子集.

可以看成一个背包大小为 sum/2 的 0-1 背包问题。

public class Solution {public boolean canPartition(int[] nums) {int sum = computeArraySum(nums);if (sum % 2 != 0) {return false;}int W = sum / 2;boolean[] dp = new boolean[W + 1];dp[0] = true;for (int num : nums) {                 // 0-1 背包一个物品只能用一次for (int i = W; i >= num; i--) {   // 从后往前，先计算 dp[i] 再计算 dp[i-num]dp[i] = dp[i] || dp[i - num];}}return dp[W];
}private int computeArraySum(int[] nums) {int sum = 0;for (int num : nums) {sum += num;}return sum;
}
}

494.目标和

给定一个非负整数数组，a1, a2, ..., an, 和一个目标数，S。现在你有两个符号 + 和 -。对于数组中的任意一个整数，

你都可以从 + 或 -中选择一个符号添加在前面。

返回可以使最终数组和为目标数 S 的所有添加符号的方法数。

示例 1:

该问题可以转换为 Subset Sum 问题，从而使用 0-1 背包的方法来求解。
可以将这组数看成两部分，P 和 N，其中 P 使用正号，N 使用负号，有以下推导：

                  sum(P) - sum(N) = target
sum(P) + sum(N) + sum(P) - sum(N) = target + sum(P) + sum(N)2 * sum(P) = target + sum(nums)
```
因此只要找到一个子集，令它们都取正号，并且和等于 (target + sum(nums))/2，就证明存在解。

class Solution {public int findTargetSumWays(int[] nums, int S) {int sum = computeArraySum(nums);if (sum < S || (sum + S) % 2 == 1) {return 0;}int W = (sum + S) / 2;int[] dp = new int[W + 1];dp[0] = 1;for (int num : nums) {for (int i = W; i >= num; i--) {dp[i] = dp[i] + dp[i - num];}}return dp[W];
}private int computeArraySum(int[] nums) {int sum = 0;for (int num : nums) {sum += num;}return sum;
}
}

474.一和零

在计算机界中，我们总是追求用有限的资源获取最大的收益。

现在，假设你分别支配着 m 个 0 和 n 个 1。另外，还有一个仅包含 0 和 1 字符串的数组。

你的任务是使用给定的 m 个 0 和 n 个 1 ，找到能拼出存在于数组中的字符串的最大数量。每个 0 和 1 至多被使用一次。

注意:

给定 0 和 1 的数量都不会超过 100。
给定字符串数组的长度不会超过 600。

这是一个多维费用的 0-1 背包问题，有两个背包大小，0 的数量和 1 的数量。

class Solution {public int findMaxForm(String[] strs, int m, int n) {if (strs == null || strs.length == 0) {return 0;}int[][] dp = new int[m + 1][n + 1];for (String s : strs) {    // 每个字符串只能用一次int ones = 0, zeros = 0;for (char c : s.toCharArray()) {if (c == '0') {zeros++;} else {ones++;}}for (int i = m; i >= zeros; i--) {for (int j = n; j >= ones; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeros][j - ones] + 1);}}}return dp[m][n];
}
}

322.零钱兑换

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。

如果没有任何一种硬币组合能组成总金额，返回 -1。

示例 1:输入: coins = [1, 2, 5], amount = 11 输出: 3 解释: 11 = 5 + 5 + 1
示例 2: 输入: coins = [2], amount = 3 输出: -1

因为硬币可以重复使用，因此这是一个完全背包问题。完全背包只需要将 0-1 背包中逆序遍历 dp 数组改为正序遍历即可。

class Solution {public int coinChange(int[] coins, int amount) {if (amount == 0 || coins == null || coins.length == 0) {return 0;}int[] dp = new int[amount + 1];for (int coin : coins) {for (int i = coin; i <= amount; i++) { //将逆序遍历改为正序遍历if (i == coin) {dp[i] = 1;} else if (dp[i] == 0 && dp[i - coin] != 0) {dp[i] = dp[i - coin] + 1;} else if (dp[i - coin] != 0) {dp[i] = Math.min(dp[i], dp[i - coin] + 1);}}}return dp[amount] == 0 ? -1 : dp[amount];
}
}

518 零钱兑换2

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

示例 1:输入: amount = 5, coins = [1, 2, 5] 输出: 4 解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2: 输入: amount = 3, coins = [2] 输出: 0 解释: 只用面额2的硬币不能凑成总金额3。

完全背包问题，使用 dp 记录可达成目标的组合数目。

class Solution {public int change(int amount, int[] coins) {//完全背包问题，用dp记录可以达成的目标的组合数目。//dp[i]表示价值为i的金额可被表示的目标组合数目。   int []dp=new int[amount+1];dp[0]=1;for(int coin:coins){for(int i=coin;i<=amount;i++){dp[i]=dp[i]+dp[i-coin];}}return dp[amount];}
}

139.单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：拆分时可以重复使用字典中的单词。你可以假设字典中没有重复的单词。

ict 中的单词没有使用次数的限制，因此这是一个完全背包问题。该问题涉及到字典中单词的使用顺序，因此可理解为涉及顺序
的完全背包问题。
求解顺序的完全背包问题时，对物品的迭代应该放在最里层。

class Solution {public boolean wordBreak(String s, List wordDict) {int n = s.length();boolean[] dp = new boolean[n + 1];dp[0] = true;for (int i = 1; i <= n; i++) {for (String word : wordDict) {   // 对物品的迭代应该放在最里层int len = word.length();if (len <= i && word.equals(s.substring(i - len, i))) {dp[i] = dp[i] || dp[i - len];}}}return dp[n];
}
}

377 组合总和IV

涉及顺序的完全背包。

class Solution {public int combinationSum4(int[] nums, int target) {if (nums == null || nums.length == 0) {return 0;}int[] maximum = new int[target + 1];maximum[0] = 1;Arrays.sort(nums);for (int i = 1; i <= target; i++) {for (int j = 0; j < nums.length && nums[j] <= i; j++) {maximum[i] += maximum[i - nums[j]];}}return maximum[target];
}
}

# 股票交易

309.最佳买卖股票时机含冷冻期

class Solution {public int maxProfit(int[] prices) {if (prices == null || prices.length == 0) {return 0;}int N = prices.length;int[] buy = new int[N];int[] s1 = new int[N];int[] sell = new int[N];int[] s2 = new int[N];s1[0] = buy[0] = -prices[0];sell[0] = s2[0] = 0;for (int i = 1; i < N; i++) {buy[i] = s2[i - 1] - prices[i];s1[i] = Math.max(buy[i - 1], s1[i - 1]);sell[i] = Math.max(buy[i - 1], s1[i - 1]) + prices[i];s2[i] = Math.max(s2[i - 1], sell[i - 1]);}return Math.max(sell[N - 1], s2[N - 1]);
}
}

714. 买卖股票的最佳时机含手续费

class Solution {public int maxProfit(int[] prices, int fee) {int cash = 0, hold = -prices[0];for (int i = 1; i < prices.length; i++) {cash = Math.max(cash, hold + prices[i] - fee);hold = Math.max(hold, cash - prices[i]);}return cash;}
}

123. 买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。

你最多可以完成两笔交易。注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

class Solution {public int maxProfit(int[] prices) {int firstBuy = Integer.MIN_VALUE, firstSell = 0;int secondBuy = Integer.MIN_VALUE, secondSell = 0;for (int curPrice : prices) {if (firstBuy < -curPrice) {firstBuy = -curPrice;}if (firstSell < firstBuy + curPrice) {firstSell = firstBuy + curPrice;}if (secondBuy < firstSell - curPrice) {secondBuy = firstSell - curPrice;}if (secondSell < secondBuy + curPrice) {secondSell = secondBuy + curPrice;}}return secondSell;
}
}

188. 买卖股票的最佳时机 IV

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）

class Solution {public int maxProfit(int k, int[] prices) {int n = prices.length;if (k >= n / 2) {   // 这种情况下该问题退化为普通的股票交易问题int maxProfit = 0;for (int i = 1; i < n; i++) {if (prices[i] > prices[i - 1]) {maxProfit += prices[i] - prices[i - 1];}}return maxProfit;}int[][] maxProfit = new int[k + 1][n];for (int i = 1; i <= k; i++) {int localMax = maxProfit[i - 1][0] - prices[0];for (int j = 1; j < n; j++) {maxProfit[i][j] = Math.max(maxProfit[i][j - 1], prices[j] + localMax);localMax = Math.max(localMax, maxProfit[i - 1][j] - prices[j]);}}return maxProfit[k][n - 1];
}
}

# 字符串编辑

583. 两个字符串的删除操作

class Solution {public int minDistance(String word1, String word2) {int m = word1.length(), n = word2.length();int[][] dp = new int[m + 1][n + 1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (word1.charAt(i - 1) == word2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;} else {dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);}}}return m + n - 2 * dp[m][n];
}
}

72. 编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

题目描述：修改一个字符串成为另一个字符串，使得修改次数最少。一次修改操作包括：插入一个字符、删除一个字符、替换一个字符。

class Solution {public int minDistance(String word1, String word2) {int n = word1.length();int m = word2.length();// if one of the strings is emptyif (n * m == 0)return n + m;// array to store the convertion historyint [][] d = new int[n + 1][m + 1];// init boundariesfor (int i = 0; i < n + 1; i++) {d[i][0] = i;}for (int j = 0; j < m + 1; j++) {d[0][j] = j;}// DP compute for (int i = 1; i < n + 1; i++) {for (int j = 1; j < m + 1; j++) {int left = d[i - 1][j] + 1;int down = d[i][j - 1] + 1;int left_down = d[i - 1][j - 1];if (word1.charAt(i - 1) != word2.charAt(j - 1))left_down += 1;d[i][j] = Math.min(left, Math.min(down, left_down));}}return d[n][m];}
}

650. 只有两个键的键盘

最初在一个记事本上只有一个字符 'A'。你每次可以对这个记事本进行两种操作：

Copy All (复制全部) : 你可以复制这个记事本中的所有字符(部分的复制是不允许的)。
Paste (粘贴) : 你可以粘贴你上一次复制的字符。
给定一个数字 n 。你需要使用最少的操作次数，在记事本中打印出恰好 n 个 'A'。输出能够打印出 n 个 'A' 的最少操作次数。

class Solution {
public int minSteps(int n) {if (n == 1) return 0;for (int i = 2; i <= Math.sqrt(n); i++) {if (n % i == 0) return i + minSteps(n / i);}return n;
}
}

双指针

* [167. 两数之和 II - 输入有序数组](#1-有序数组的-two-sum)
* [633.平方数之和](#2-两数平方和)
* [345. 反转字符串中的元音字母](#3-反转字符串中的元音字符)
* [680. 验证回文字符串 Ⅱ](#4-回文字符串)
* [88. 合并两个有序数组](#5-归并两个有序数组)
* [141. 环形链表](#6-判断链表是否存在环)
* [524. 通过删除字母匹配到字典里最长单词](#7-最长子序列)

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。

167. 两数之和 II - 输入有序数组

给定一个已按照升序排列的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

使用双指针，一个指针指向值较小的元素，一个指针指向值较大的元素。指向较小元素的指针从头向尾遍历，指向较大元素的指针
从尾向头遍历。- 如果两个指针指向元素的和 sum == target，那么得到要求的结果；
- 如果 sum > target，移动较大的元素，使 sum 变小一些；
- 如果 sum < target，移动较小的元素，使 sum 变大一些。

class Solution {public int[] twoSum(int[] numbers, int target) {int i = 0, j = numbers.length - 1;while (i < j) {int sum = numbers[i] + numbers[j];if (sum == target) {return new int[]{i + 1, j + 1};} else if (sum < target) {i++;} else {j--;}}return null;
}
}

633.平方数之和

给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得 a2 + b2 = c。

示例1: 输入: 5 输出: True 解释: 1 * 1 + 2 * 2 = 5
示例2: 输入: 3 输出: False

class Solution {public boolean judgeSquareSum(int c) {int i = 0, j = (int) Math.sqrt(c);while (i <= j) {int powSum = i * i + j * j;if (powSum == c) {return true;} else if (powSum > c) {j--;} else {i++;}}return false;
}
}

345. 反转字符串中的元音字母

编写一个函数，以字符串作为输入，反转该字符串中的元音字母。

示例 1: 输入: "hello" 输出: "holle"
示例 2: 输入: "leetcode" 输出: "leotcede"

class Solution {private final static HashSet vowels = new HashSet<>(Arrays.asList('a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'));public String reverseVowels(String s) {int i = 0, j = s.length() - 1;char[] result = new char[s.length()];while (i <= j) {char ci = s.charAt(i);char cj = s.charAt(j);if (!vowels.contains(ci)) {result[i++] = ci;} else if (!vowels.contains(cj)) {result[j--] = cj;} else {result[i++] = cj;result[j--] = ci;}}return new String(result);
}
}

680. 验证回文字符串 Ⅱ

给定一个非空字符串 s，最多删除一个字符。判断是否能成为回文字符串。

示例 1: 输入: "aba" 输出: True

示例 2: 输入: "abca" 输出: True 解释: 你可以删除c字符。

题目描述：可以删除一个字符，判断是否能构成回文字符串。

class Solution {
public boolean validPalindrome(String s) {int left=0;int right=s.length()-1;//"abca"while(left

 
88. 合并两个有序数组 
给定两个有序整数数组 nums1 和 nums2，将 nums2 合并到 nums1 中，使得 num1 成为一个有序数组。 
说明: 
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间（空间大小大于或等于 m + n）来保存 nums2 中的元素。 
输入:
 nums1 = [1,2,3,0,0,0], m = 3
 nums2 = [2,5,6],       n = 3 
输出: [1,2,2,3,5,6] 
class Solution {public void merge(int[] nums1, int m, int[] nums2, int n) {int index1 = m - 1, index2 = n - 1;int indexMerge = m + n - 1;while (index1 >= 0 || index2 >= 0) {if (index1 < 0) {nums1[indexMerge--] = nums2[index2--];} else if (index2 < 0) {nums1[indexMerge--] = nums1[index1--];} else if (nums1[index1] > nums2[index2]) {nums1[indexMerge--] = nums1[index1--];} else {nums1[indexMerge--] = nums2[index2--];}}
}
} 
141. 环形链表 
给定一个链表，判断链表中是否有环。 
 
/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public boolean hasCycle(ListNode head) {if(head==null||head.next==null){return false;}ListNode p1 = head;ListNode p2 = head;while(p2!=null&&p2.next!=null){p1 = p1.next;p2 = p2.next.next;if(p1==p2){return true;}}return false;}
} 
524. 通过删除字母匹配到字典里最长单词 
给定一个字符串和一个字符串字典，找到字典里面最长的字符串，该字符串可以通过删除给定字符串的某些字符来得到。 
如果答案不止一个，返回长度最长且字典顺序最小的字符串。如果答案不存在，则返回空字符串。 
示例 1:输入: s = "abpcplea", d = ["ale","apple","monkey","plea"]  输出: "apple"
 示例 2:输入: s = "abpcplea", d = ["a","b","c"] 输出:  "a" 
class Solution {public String findLongestWord(String s, List d) {String longestWord = "";for (String target : d) {int l1 = longestWord.length(), l2 = target.length();if (l1 > l2 || (l1 == l2 && longestWord.compareTo(target) < 0)) {continue;}if (isSubstr(s, target)) {longestWord = target;}}return longestWord;
}private boolean isSubstr(String s, String target) {int i = 0, j = 0;while (i < s.length() && j < target.length()) {if (s.charAt(i) == target.charAt(j)) {j++;}i++;}return j == target.length();
}
} 
哈希表 
* [1. 两数之和](#1-数组中两个数的和为给定值)
* [217. 存在重复元素](#2-判断数组是否含有重复元素)
* [594. 最长和谐子序列](#3-最长和谐序列)
* [128. 最长连续序列](#4-最长连续序列) 
1. 两数之和 
给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。 
给定 nums = [2, 7, 11, 15], target = 9 
因为 nums[0] + nums[1] = 2 + 7 = 9
 所以返回 [0, 1] 
class Solution {public int[] twoSum(int[] nums, int target) {Map map = new HashMap<>();for(int i = 0; i
 
217. 存在重复元素 
给定一个整数数组，判断是否存在重复元素。 
示例 1:  输入: [1,2,3,1]  输出: true
 示例 2:  输入: [1,2,3,4]  输出: false
 示例 3: 输入: [1,1,1,3,3,4,3,2,4,2]   输出: true 
class Solution {public boolean containsDuplicate(int[] nums) {Set set = new HashSet<>();for (int num : nums) {set.add(num);}return set.size() < nums.length;
}
} 
594. 最长和谐子序列 
和谐数组是指一个数组里元素的最大值和最小值之间的差别正好是1。 
现在，给定一个整数数组，你需要在所有可能的子序列中找到最长的和谐子序列的长度。 
输入: [1,3,2,2,5,2,3,7]
输出: 5
原因: 最长的和谐数组是：[3,2,2,2,3]. 
class Solution {
public int findLHS(int[] nums) {Map countForNum = new HashMap<>();for (int num : nums) {countForNum.put(num, countForNum.getOrDefault(num, 0) + 1);}int longest = 0;for (int num : countForNum.keySet()) {if (countForNum.containsKey(num + 1)) {longest = Math.max(longest, countForNum.get(num + 1) + countForNum.get(num));}}return longest;
}} 
128. 最长连续序列 
给定一个未排序的整数数组，找出最长连续序列的长 
输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是  [1, 2, 3, 4]。它的长度为 4。
 
class Solution {public int longestConsecutive(int[] nums) {Set num_set = new HashSet();for (int num : nums) {num_set.add(num);}int longestStreak = 0;for (int num : num_set) {if (!num_set.contains(num-1)) {int currentNum = num;int currentStreak = 1;while (num_set.contains(currentNum+1)) {currentNum += 1;currentStreak += 1;}longestStreak = Math.max(longestStreak, currentStreak);}}return longestStreak;}
} 
图 
* [二分图](#二分图)* [785. 判断二分图](#1-判断是否为二分图)
* [拓扑排序](#拓扑排序)* [207. 课程表](#1-课程安排的合法性)* [210.课程表2](#2-课程安排的顺序)
* [并查集](#并查集)* [684.冗余连接](#1-冗余连接)785. 判断二分图 
给定一个无向图graph，当这个图为二分图时返回true。 
如果我们能将一个图的节点集合分割成两个独立的子集A和B，并使图中的每一条边的两个节点一个来自A集合， 
一个来自B集合，我们就将这个图称为二分图。 
   
class Solution {public boolean isBipartite(int[][] graph) {int[] colors = new int[graph.length];Arrays.fill(colors, -1);for (int i = 0; i < graph.length; i++) {  // 处理图不是连通的情况if (colors[i] == -1 && !isBipartite(i, 0, colors, graph)) {return false;}}return true;
}private boolean isBipartite(int curNode, int curColor, int[] colors, int[][] graph) {if (colors[curNode] != -1) {return colors[curNode] == curColor;}colors[curNode] = curColor;for (int nextNode : graph[curNode]) {if (!isBipartite(nextNode, 1 - curColor, colors, graph)) {return false;}}return true;
}
} 
# 拓扑排序   常用于在具有先序关系的任务规划中。 
207. 课程表 
现在你总共有 n 门课需要选，记为 0 到 n-1。 
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1] 
给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？ 
示例 1:   输入: 2, [[1,0]]   输出: true
 解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。
 示例 2:   输入: 2, [[1,0],[0,1]]  输出: false
 解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。 
class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {List[] graphic = new List[numCourses];for (int i = 0; i < numCourses; i++) {graphic[i] = new ArrayList<>();}for (int[] pre : prerequisites) {graphic[pre[0]].add(pre[1]);}boolean[] globalMarked = new boolean[numCourses];boolean[] localMarked = new boolean[numCourses];for (int i = 0; i < numCourses; i++) {if (hasCycle(globalMarked, localMarked, graphic, i)) {return false;}}return true;
}private boolean hasCycle(boolean[] globalMarked, boolean[] localMarked,List[] graphic, int curNode) {if (localMarked[curNode]) {return true;}if (globalMarked[curNode]) {return false;}globalMarked[curNode] = true;localMarked[curNode] = true;for (int nextNode : graphic[curNode]) {if (hasCycle(globalMarked, localMarked, graphic, nextNode)) {return true;}}localMarked[curNode] = false;return false;
}
} 
210.课程表2 
现在你总共有 n 门课需要选，记为 0 到 n-1。 
在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示 
他们: [0,1]给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。 
可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。 
示例 1: 
输入: 2, [[1,0]] 
 输出: [0,1]
 解释: 总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。
 示例 2: 
输入: 4, [[1,0],[2,0],[3,1],[3,2]]
 输出: [0,1,2,3] or [0,2,1,3]
 解释: 总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
      因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。 
class Solution {public int[] findOrder(int numCourses, int[][] prerequisites) {List[] graphic = new List[numCourses];for (int i = 0; i < numCourses; i++) {graphic[i] = new ArrayList<>();}for (int[] pre : prerequisites) {graphic[pre[0]].add(pre[1]);}Stack postOrder = new Stack<>();boolean[] globalMarked = new boolean[numCourses];boolean[] localMarked = new boolean[numCourses];for (int i = 0; i < numCourses; i++) {if (hasCycle(globalMarked, localMarked, graphic, i, postOrder)) {return new int[0];}}int[] orders = new int[numCourses];for (int i = numCourses - 1; i >= 0; i--) {orders[i] = postOrder.pop();}return orders;
}private boolean hasCycle(boolean[] globalMarked, boolean[] localMarked, List[] graphic,int curNode, Stack postOrder) {if (localMarked[curNode]) {return true;}if (globalMarked[curNode]) {return false;}globalMarked[curNode] = true;localMarked[curNode] = true;for (int nextNode : graphic[curNode]) {if (hasCycle(globalMarked, localMarked, graphic, nextNode, postOrder)) {return true;}}localMarked[curNode] = false;postOrder.push(curNode);return false;
}
} 
684.冗余连接 
在本问题中, 树指的是一个连通且无环的无向图。 
输入一个图，该图由一个有着N个节点 (节点值不重复1, 2, ..., N) 的树及一条附加的边构成。附加的边的两个顶点 
包含在1到N中间，这条附加的边不属于树中已存在的边。 
结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ，满足 u < v，表示连接顶点u 和v的无向图的边。 
返回一条可以删去的边，使得结果图是一个有着N个节点的树。如果有多个答案，则返回二维数组中最后出现的边。 
答案边 [u, v] 应满足相同的格式 u < v。 
示例 1：输入: [[1,2], [1,3], [2,3]]  输出: [2,3]
 解释: 给定的无向图为:
   1
  / \
 2 - 3
 示例 2： 
输入: [[1,2], [2,3], [3,4], [1,4], [1,5]]   输出: [1,4]
 解释: 给定的无向图为:
 5 - 1 - 2
     |   |
     4 - 3 
public class Solution{ 
public int[] findRedundantConnection(int[][] edges) {int n = edges.length;int[] pre = new int[n + 1];//每个pre节点初始化为自己for(int i = 0;i<= n;i++){pre[i] = i;}for(int[] arr : edges){int root1 = findRoot(arr[0],pre);int root2 = findRoot(arr[1],pre);//arr边的两个节点arr[0],arr[1]有共同的根节点，说明在一个连通子图中，
此时这条边不能加入，否则会形成环，因此这条边需要删去if(root1 == root2){return arr;}//并集，将root1下所有子节点的根节点设为root2，方便下次寻找根节点adjust(arr[0],root2,pre);}return new int[0];}//寻找该节点的根节点private int findRoot(int num,int[] pre){while(pre[num] != num){num = pre[num];}return num;}//并集 + 路径压缩private void adjust(int x,int root,int[] pre){while(pre[x] != root){int temp = pre[x];pre[x] = root;x = temp;}}
} 
字符串 
* [242. 有效的字母异位词](#4-两个字符串包含的字符是否完全相同)
* [409 最长回文串](#5-计算一组字符集合可以组成的回文字符串的最大长度)
* [205. 同构字符串](#6-字符串同构)
* [647. 回文子串](#7-回文子字符串个数)
* [9. 回文数](#8-判断一个整数是否是回文数)
* [696.计算二进制子串](#9-统计二进制字符串中连续-1-和连续-0-数量相同的子字符串个数) 
242. 有效的字母异位词 
 
class Solution {public boolean isAnagram(String s, String t) {int[] cnts = new int[26];for (char c : s.toCharArray()) {cnts[c - 'a']++;}for (char c : t.toCharArray()) {cnts[c - 'a']--;}for (int cnt : cnts) {if (cnt != 0) {return false;}}return true;
}
} 
409 最长回文串 
 
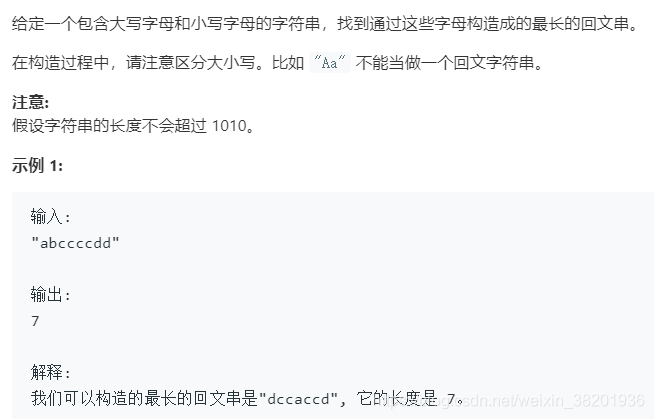
class Solution {public int longestPalindrome(String s) {int[] cnts = new int[256];for (char c : s.toCharArray()) {cnts[c]++;}int palindrome = 0;for (int cnt : cnts) {palindrome += (cnt / 2) * 2;}if (palindrome < s.length()) {palindrome++;   // 这个条件下 s 中一定有单个未使用的字符存在，可以把这个字符放到回文的最中间}return palindrome;
}
} 
205. 同构字符串 
 
class Solution {private int cnt = 0;public int countSubstrings(String s) {for (int i = 0; i < s.length(); i++) {extendSubstrings(s, i, i);     // 奇数长度extendSubstrings(s, i, i + 1); // 偶数长度}return cnt;
}private void extendSubstrings(String s, int start, int end) {while (start >= 0 && end < s.length() && s.charAt(start) == s.charAt(end)) {start--;end++;cnt++;}
}
} 
9. 回文数 
 
class Solution {public boolean isPalindrome(int x) {if (x == 0) {return true;}if (x < 0 || x % 10 == 0) {return false;}int right = 0;while (x > right) {right = right * 10 + x % 10;x /= 10;}return x == right || x == right / 10;
}
} 
696.计算二进制子串 
 
class Solution {public int countBinarySubstrings(String s) {int preLen = 0, curLen = 1, count = 0;for (int i = 1; i < s.length(); i++) {if (s.charAt(i) == s.charAt(i - 1)) {curLen++;} else {preLen = curLen;curLen = 1;}if (preLen >= curLen) {count++;}}return count;
}
} 
排序 
* [快速选择](#快速选择)
* [堆](#堆)* [215. 数组中的第K个最大元素](#1-kth-element)
* [桶排序](#桶排序)* [347. 前 K 个高频元素](#1-出现频率最多的-k-个元素)* [451. 根据字符出现频率排序](#2-按照字符出现次数对字符串排序)
* [荷兰国旗问题](#荷兰国旗问题)* [75. 颜色分类](#1-按颜色进行排序) 
# 快速选择用于求解  **Kth Element**  问题，也就是第 K 个元素的问题。可以使用快速排序的 partition() 进行实现。需要先打乱数组，否则最坏情况下时间复杂度为 O(N²)。 
# 堆用于求解  **TopK Elements**  问题，也就是 K 个最小元素的问题。可以维护一个大小为 K 的最小堆，最小堆中的元素
就是最小元素。最小堆需要使用大顶堆来实现，大顶堆表示堆顶元素是堆中最大元素。这是因为我们要得到 k 个最小的元素，
因此当遍历到一个新的元素时，需要知道这个新元素是否比堆中最大的元素更小，更小的话就把堆中最大元素去除，并将新元素
添加到堆中。所以我们需要很容易得到最大元素并移除最大元素，大顶堆就能很好满足这个要求。
堆也可以用于求解 Kth Element 问题，得到了大小为 k 的最小堆之后，因为使用了大顶堆来实现，因此堆顶元素就是第 k 大的元素。
快速选择也可以求解 TopK Elements 问题，因为找到 Kth Element 之后，再遍历一次数组，所有小于等于 Kth Element 的
元素都是 TopK Elements。
可以看到，快速选择和堆排序都可以求解 Kth Element 和 TopK Elements 问题。 
215. 数组中的第K个最大元素 
 
class Solution {public int findKthLargest(int[] nums, int k) {Arrays.sort(nums);return nums[nums.length - k];
}
} 
347. 前 K 个高频元素 
 
设置若干个桶，每个桶存储出现频率相同的数。桶的下标表示数出现的频率，即第 i 个桶中存储的数出现的频率为 i。把数都放到桶之后，从后向前遍历桶，最先得到的 k 个数就是出现频率最多的的 k 个数。 
class Solution {public List topKFrequent(int[] nums, int k) {Map frequencyForNum = new HashMap<>();for (int num : nums) {frequencyForNum.put(num, frequencyForNum.getOrDefault(num, 0) + 1);}List[] buckets = new ArrayList[nums.length + 1];for (int key : frequencyForNum.keySet()) {int frequency = frequencyForNum.get(key);if (buckets[frequency] == null) {buckets[frequency] = new ArrayList<>();}buckets[frequency].add(key);}List topK = new ArrayList<>();for (int i = buckets.length - 1; i >= 0 && topK.size() < k; i--) {if (buckets[i] == null) {continue;}if (buckets[i].size() <= (k - topK.size())) {topK.addAll(buckets[i]);} else {topK.addAll(buckets[i].subList(0, k - topK.size()));}}return topK;
}
} 
451. 根据字符出现频率排序 
 
class Solution {public String frequencySort(String s) {Map frequencyForNum = new HashMap<>();for (char c : s.toCharArray())frequencyForNum.put(c, frequencyForNum.getOrDefault(c, 0) + 1);List[] frequencyBucket = new ArrayList[s.length() + 1];for (char c : frequencyForNum.keySet()) {int f = frequencyForNum.get(c);if (frequencyBucket[f] == null) {frequencyBucket[f] = new ArrayList<>();}frequencyBucket[f].add(c);}StringBuilder str = new StringBuilder();for (int i = frequencyBucket.length - 1; i >= 0; i--) {if (frequencyBucket[i] == null) {continue;}for (char c : frequencyBucket[i]) {for (int j = 0; j < i; j++) {str.append(c);}}}return str.toString();
}
} 
# 荷兰国旗问题荷兰国旗包含三种颜色：红、白、蓝。有三种颜色的球，算法的目标是将这三种球按颜色顺序正确地排列。它其实是三向切分快速排序的一种变种，在三向切分快速排序中，
每次切分都将数组分成三个区间：小于切分元素、等于切分元素、大于切分元素，而该算法是将数组分成三个区间：等于红色、
等于白色、等于蓝色。
 
75. 颜色分类 
 
class Solution {public void sortColors(int[] nums) {int zero = -1, one = 0, two = nums.length;while (one < two) {if (nums[one] == 0) {swap(nums, ++zero, one++);} else if (nums[one] == 2) {swap(nums, --two, one);} else {++one;}}
}private void swap(int[] nums, int i, int j) {int t = nums[i];nums[i] = nums[j];nums[j] = t;
}
} 
搜索 
 
class Solution {public int numSquares(int n) {List squareList = generateSquareList(n);int[] dp = new int[n + 1];for (int i = 1; i <= n; i++) {int min = Integer.MAX_VALUE;for (int square : squareList) {if (square > i) {break;}min = Math.min(min, dp[i - square] + 1);}dp[i] = min;}return dp[n];
}private List generateSquareList(int n) {List squareList = new ArrayList<>();int diff = 3;int square = 1;while (square <= n) {squareList.add(square);square += diff;diff += 2;}return squareList;
}
} 
127. 单词接龙 
给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则： 
每次转换只能改变一个字母。
 转换过程中的中间单词必须是字典中的单词。 
示例 1: 
输入:
 beginWord = "hit",
 endWord = "cog",
 wordList = ["hot","dot","dog","lot","log","cog"] 
输出: 5 
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",  返回它的长度 5。 
import javafx.util.Pair;class Solution {public int ladderLength(String beginWord, String endWord, List wordList) {// Since all words are of same length.int L = beginWord.length();// Dictionary to hold combination of words that can be formed,// from any given word. By changing one letter at a time.HashMap> allComboDict = new HashMap>();wordList.forEach(word -> {for (int i = 0; i < L; i++) {String newWord = word.substring(0, i) + '*' + word.substring(i + 1, L);ArrayList transformations =allComboDict.getOrDefault(newWord, new ArrayList());transformations.add(word);allComboDict.put(newWord, transformations);}});// Queue for BFSQueue> Q = new LinkedList>();Q.add(new Pair(beginWord, 1));// Visited to make sure we don't repeat processing same word.HashMap visited = new HashMap();visited.put(beginWord, true);while (!Q.isEmpty()) {Pair node = Q.remove();String word = node.getKey();int level = node.getValue();for (int i = 0; i < L; i++) {// Intermediate words for current wordString newWord = word.substring(0, i) + '*' + word.substring(i + 1, L);// Next states are all the words which share the same intermediate state.for (String adjacentWord : allComboDict.getOrDefault(newWord, new ArrayList())) {if (adjacentWord.equals(endWord)) {return level + 1;}// Otherwise, add it to the BFS Queue. Also mark it visitedif (!visited.containsKey(adjacentWord)) {visited.put(adjacentWord, true);Q.add(new Pair(adjacentWord, level + 1));}}}}return 0;}
} 
695. 岛屿的最大面积 
 
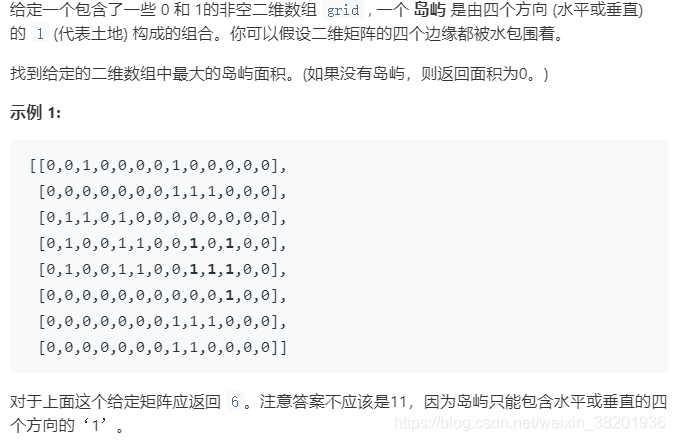
class Solution {private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int maxAreaOfIsland(int[][] grid) {if (grid == null || grid.length == 0) {return 0;}m = grid.length;n = grid[0].length;int maxArea = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {maxArea = Math.max(maxArea, dfs(grid, i, j));}}return maxArea;
}private int dfs(int[][] grid, int r, int c) {if (r < 0 || r >= m || c < 0 || c >= n || grid[r][c] == 0) {return 0;}grid[r][c] = 0;int area = 1;for (int[] d : direction) {area += dfs(grid, r + d[0], c + d[1]);}return area;
}
} 
 
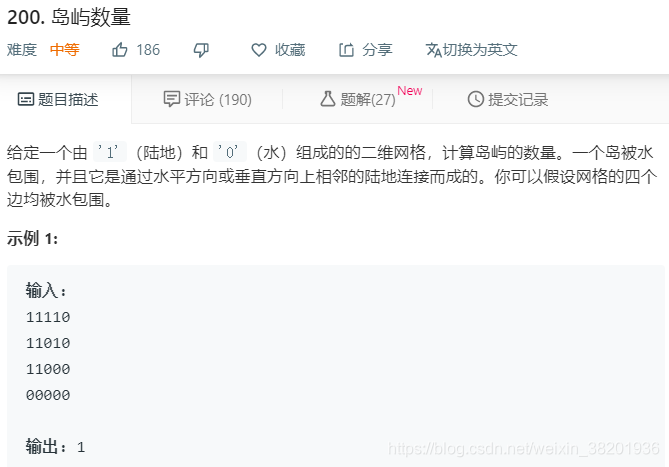
class Solution {private int m, n;
private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public int numIslands(char[][] grid) {if (grid == null || grid.length == 0) {return 0;}m = grid.length;n = grid[0].length;int islandsNum = 0;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] != '0') {dfs(grid, i, j);islandsNum++;}}}return islandsNum;
}private void dfs(char[][] grid, int i, int j) {if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == '0') {return;}grid[i][j] = '0';for (int[] d : direction) {dfs(grid, i + d[0], j + d[1]);}
}
} 
547. 朋友圈 
 
class Solution {private int n;public int findCircleNum(int[][] M) {n = M.length;int circleNum = 0;boolean[] hasVisited = new boolean[n];for (int i = 0; i < n; i++) {if (!hasVisited[i]) {dfs(M, i, hasVisited);circleNum++;}}return circleNum;
}private void dfs(int[][] M, int i, boolean[] hasVisited) {hasVisited[i] = true;for (int k = 0; k < n; k++) {if (M[i][k] == 1 && !hasVisited[k]) {dfs(M, k, hasVisited);}}
}
} 
130. 被围绕的区域 
 
class Solution {private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
private int m, n;public void solve(char[][] board) {if (board == null || board.length == 0) {return;}m = board.length;n = board[0].length;for (int i = 0; i < m; i++) {dfs(board, i, 0);dfs(board, i, n - 1);}for (int i = 0; i < n; i++) {dfs(board, 0, i);dfs(board, m - 1, i);}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (board[i][j] == 'T') {board[i][j] = 'O';} else if (board[i][j] == 'O') {board[i][j] = 'X';}}}
}private void dfs(char[][] board, int r, int c) {if (r < 0 || r >= m || c < 0 || c >= n || board[r][c] != 'O') {return;}board[r][c] = 'T';for (int[] d : direction) {dfs(board, r + d[0], c + d[1]);}
}
} 
417. 太平洋大西洋水流问题 
 
class Solution {public List pacificAtlantic(int[][] matrix) {List res=new ArrayList<>();if(matrix==null||matrix.length==0)return res;boolean[][] can1=new boolean[matrix.length][matrix[0].length];//记录能到太平洋的boolean[][] can2=new boolean[matrix.length][matrix[0].length];//记录能到大西洋的for (int i=0;i=matrix.length||jj>=matrix[0].length||can[ii][jj]){continue;}if(matrix[ii][jj]>=matrix[i][j]){dfs(can,ii,jj,matrix);}}}
} 
17. 电话号码的字母组合 
 
class Solution {private static final String[] KEYS = {"", "", "abc", "def", 
"ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};public List letterCombinations(String digits) {List combinations = new ArrayList<>();if (digits == null || digits.length() == 0) {return combinations;}doCombination(new StringBuilder(), combinations, digits);return combinations;
}private void doCombination(StringBuilder prefix, List combinations, final String digits) {if (prefix.length() == digits.length()) {combinations.add(prefix.toString());return;}int curDigits = digits.charAt(prefix.length()) - '0';String letters = KEYS[curDigits];for (char c : letters.toCharArray()) {prefix.append(c);                         // 添加doCombination(prefix, combinations, digits);prefix.deleteCharAt(prefix.length() - 1); // 删除}
}
} 
 
class Solution {public List restoreIpAddresses(String s) {List addresses = new ArrayList<>();StringBuilder tempAddress = new StringBuilder();doRestore(0, tempAddress, addresses, s);return addresses;
}private void doRestore(int k, StringBuilder tempAddress, List addresses, String s) {if (k == 4 || s.length() == 0) {if (k == 4 && s.length() == 0) {addresses.add(tempAddress.toString());}return;}for (int i = 0; i < s.length() && i <= 2; i++) {if (i != 0 && s.charAt(0) == '0') {break;}String part = s.substring(0, i + 1);if (Integer.valueOf(part) <= 255) {if (tempAddress.length() != 0) {part = "." + part;}tempAddress.append(part);doRestore(k + 1, tempAddress, addresses, s.substring(i + 1));tempAddress.delete(tempAddress.length() - part.length(), tempAddress.length());}}
}
} 
79. 单词搜索 
给定一个二维网格和一个单词，找出该单词是否存在于网格中。 
单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。 
同一个单元格内的字母不允许被重复使用。 
 
class Solution {private final static int[][] direction = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
private int m;
private int n;
public boolean exist(char[][] board, String word) {if (word == null || word.length() == 0) {return true;}if (board == null || board.length == 0 || board[0].length == 0) {return false;}m = board.length;n = board[0].length;boolean[][] hasVisited = new boolean[m][n];for (int r = 0; r < m; r++) {for (int c = 0; c < n; c++) {if (backtracking(0, r, c, hasVisited, board, word)) {return true;}}}return false;
}
private boolean backtracking(int curLen, int r, int c, boolean[][] visited, 
final char[][] board, final String word) {if (curLen == word.length()) {return true;}if (r < 0 || r >= m || c < 0 || c >= n|| board[r][c] != word.charAt(curLen) || visited[r][c]) {return false;}visited[r][c] = true;for (int[] d : direction) {if (backtracking(curLen + 1, r + d[0], c + d[1], visited, board, word)) {return true;}}visited[r][c] = false;return false;
}
} 
257. 二叉树的所有路径 
给定一个二叉树，返回所有从根节点到叶子节点的路径。 
说明: 叶子节点是指没有子节点的节点。 
 
/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode(int x) { val = x; }* }*/
class Solution {public List binaryTreePaths(TreeNode root) {List paths = new ArrayList<>();if (root == null) {return paths;}List values = new ArrayList<>();backtracking(root, values, paths);return paths;
}private void backtracking(TreeNode node, List values, List paths) {if (node == null) {return;}values.add(node.val);if (isLeaf(node)) {paths.add(buildPath(values));} else {backtracking(node.left, values, paths);backtracking(node.right, values, paths);}values.remove(values.size() - 1);
}private boolean isLeaf(TreeNode node) {return node.left == null && node.right == null;
}private String buildPath(List values) {StringBuilder str = new StringBuilder();for (int i = 0; i < values.size(); i++) {str.append(values.get(i));if (i != values.size() - 1) {str.append("->");}}return str.toString();
}
} 
46. 全排列 
 
class Solution {public List> permute(int[] nums) {List> permutes = new ArrayList<>();List permuteList = new ArrayList<>();boolean[] hasVisited = new boolean[nums.length];backtracking(permuteList, permutes, hasVisited, nums);return permutes;
}private void backtracking(List permuteList, List> permutes, boolean[] visited, final int[] nums) {if (permuteList.size() == nums.length) {permutes.add(new ArrayList<>(permuteList)); // 重新构造一个 Listreturn;}for (int i = 0; i < visited.length; i++) {if (visited[i]) {continue;}visited[i] = true;permuteList.add(nums[i]);backtracking(permuteList, permutes, visited, nums);permuteList.remove(permuteList.size() - 1);visited[i] = false;}
}
} 
47. 全排列 II 
给定一个可包含重复数字的序列，返回所有不重复的全排列。 
示例: 
输入: [1,1,2]
 输出:
 [
   [1,1,2],
   [1,2,1],
   [2,1,1]
 ] 
class Solution {public List> permuteUnique(int[] nums) {List> permutes = new ArrayList<>();List permuteList = new ArrayList<>();Arrays.sort(nums);  // 排序boolean[] hasVisited = new boolean[nums.length];backtracking(permuteList, permutes, hasVisited, nums);return permutes;
}private void backtracking(List permuteList, 
List> permutes, boolean[] visited, final int[] nums) {if (permuteList.size() == nums.length) {permutes.add(new ArrayList<>(permuteList));return;}for (int i = 0; i < visited.length; i++) {if (i != 0 && nums[i] == nums[i - 1] && !visited[i - 1]) {continue;  // 防止重复}if (visited[i]){continue;}visited[i] = true;permuteList.add(nums[i]);backtracking(permuteList, permutes, visited, nums);permuteList.remove(permuteList.size() - 1);visited[i] = false;}
}
} 
77 组合 
给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。 
 
class Solution {public List> combine(int n, int k) {List> combinations = new ArrayList<>();List combineList = new ArrayList<>();backtracking(combineList, combinations, 1, k, n);return combinations;
}private void backtracking(List combineList, List> 
combinations, int start, int k, final int n) {if (k == 0) {combinations.add(new ArrayList<>(combineList));return;}for (int i = start; i <= n - k + 1; i++) {  // 剪枝combineList.add(i);backtracking(combineList, combinations, i + 1, k - 1, n);combineList.remove(combineList.size() - 1);}
}
} 
39. 组合总和 
给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 
candidates 中的数字可以无限制重复被选取。 
 
class Solution {public List> combinationSum(int[] candidates, int target) {List> combinations = new ArrayList<>();backtracking(new ArrayList<>(), combinations, 0, target, candidates);return combinations;
}private void backtracking(List tempCombination, List> combinations,int start, int target, final int[] candidates) {if (target == 0) {combinations.add(new ArrayList<>(tempCombination));return;}for (int i = start; i < candidates.length; i++) {if (candidates[i] <= target) {tempCombination.add(candidates[i]);backtracking(tempCombination, combinations, i, target - candidates[i], candidates);tempCombination.remove(tempCombination.size() - 1);}}
}
} 
40. 组合总和 II 
给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。 
candidates 中的每个数字在每个组合中只能使用一次。 
 
class Solution {public List> combinationSum2(int[] candidates, int target) {List> combinations = new ArrayList<>();Arrays.sort(candidates);backtracking(new ArrayList<>(), combinations, 
new boolean[candidates.length], 0, target, candidates);return combinations;
}private void backtracking(List tempCombination, List> combinations,boolean[] hasVisited, int start, int target, final int[] candidates) {if (target == 0) {combinations.add(new ArrayList<>(tempCombination));return;}for (int i = start; i < candidates.length; i++) {if (i != 0 && candidates[i] == candidates[i - 1] && !hasVisited[i - 1]) {continue;}if (candidates[i] <= target) {tempCombination.add(candidates[i]);hasVisited[i] = true;backtracking(tempCombination, combinations, hasVisited, i + 1,target - candidates[i], candidates);hasVisited[i] = false;tempCombination.remove(tempCombination.size() - 1);}}
}
} 
216. 组合总和 III 
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。 
说明： 
所有数字都是正整数。
 解集不能包含重复的组合。  
 
public List> combinationSum3(int k, int n) {List> combinations = new ArrayList<>();List path = new ArrayList<>();backtracking(k, n, 1, path, combinations);return combinations;
}private void backtracking(int k, int n, int start,List tempCombination, List> combinations) {if (k == 0 && n == 0) {combinations.add(new ArrayList<>(tempCombination));return;}if (k == 0 || n == 0) {return;}for (int i = start; i <= 9; i++) {tempCombination.add(i);backtracking(k - 1, n - i, i + 1, tempCombination, combinations);tempCombination.remove(tempCombination.size() - 1);}
} 
78. 子集 
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。 
说明：解集不能包含重复的子集。 
 
class Solution {public List> subsets(int[] nums) {List> subsets = new ArrayList<>();List tempSubset = new ArrayList<>();for (int size = 0; size <= nums.length; size++) {backtracking(0, tempSubset, subsets, size, nums); // 不同的子集大小}return subsets;
}private void backtracking(int start, List tempSubset, List> subsets,final int size, final int[] nums) {if (tempSubset.size() == size) {subsets.add(new ArrayList<>(tempSubset));return;}for (int i = start; i < nums.length; i++) {tempSubset.add(nums[i]);backtracking(i + 1, tempSubset, subsets, size, nums);tempSubset.remove(tempSubset.size() - 1);}
}
} 
78. 子集 
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。 
说明：解集不能包含重复的子集。 
class Solution {public List> subsets(int[] nums) {List> subsets = new ArrayList<>();List tempSubset = new ArrayList<>();for (int size = 0; size <= nums.length; size++) {backtracking(0, tempSubset, subsets, size, nums); // 不同的子集大小}return subsets;
}private void backtracking(int start, List tempSubset, List> subsets,final int size, final int[] nums) {if (tempSubset.size() == size) {subsets.add(new ArrayList<>(tempSubset));return;}for (int i = start; i < nums.length; i++) {tempSubset.add(nums[i]);backtracking(i + 1, tempSubset, subsets, size, nums);tempSubset.remove(tempSubset.size() - 1);}
}
} 
90. 子集 II 
给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。 
说明：解集不能包含重复的子集。 
输入: [1,2,2]
输出:
[[2],[1],[1,2,2],[2,2],[1,2],[]
] 
class Solution {public List> subsetsWithDup(int[] nums) {Arrays.sort(nums);List> subsets = new ArrayList<>();List tempSubset = new ArrayList<>();boolean[] hasVisited = new boolean[nums.length];for (int size = 0; size <= nums.length; size++) {backtracking(0, tempSubset, subsets, hasVisited, size, nums); // 不同的子集大小}return subsets;
}private void backtracking(int start, List tempSubset, 
List> subsets, boolean[] hasVisited,final int size, final int[] nums) {if (tempSubset.size() == size) {subsets.add(new ArrayList<>(tempSubset));return;}for (int i = start; i < nums.length; i++) {if (i != 0 && nums[i] == nums[i - 1] && !hasVisited[i - 1]) {continue;}tempSubset.add(nums[i]);hasVisited[i] = true;backtracking(i + 1, tempSubset, subsets, hasVisited, size, nums);hasVisited[i] = false;tempSubset.remove(tempSubset.size() - 1);}
}
} 
131. 分割回文串 
 
 
class Solution {List>list=new ArrayList<>();String s;public List> partition(String s) {//从头到尾递归+回溯。this.s=s;//这个是满足的每一个集合Listll=new ArrayList<>();dfs(ll,0);return list;}public void dfs(Listll,int index){if(index==s.length()){list.add(new ArrayList<>(ll));return;}//i从index开始是因为单个字符也是回文子串for(int i=index;i
 
37. 解数独 
编写一个程序，通过已填充的空格来解决数独问题。 
一个数独的解法需遵循如下规则： 
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
空白格用 '.' 表示。 
 
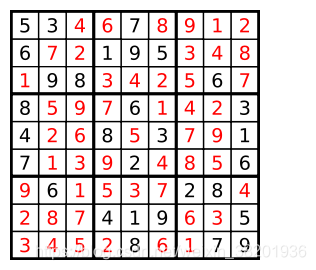
class Solution {private boolean[][] rowsUsed = new boolean[9][10];
private boolean[][] colsUsed = new boolean[9][10];
private boolean[][] cubesUsed = new boolean[9][10];
private char[][] board;public void solveSudoku(char[][] board) {this.board = board;for (int i = 0; i < 9; i++)for (int j = 0; j < 9; j++) {if (board[i][j] == '.') {continue;}int num = board[i][j] - '0';rowsUsed[i][num] = true;colsUsed[j][num] = true;cubesUsed[cubeNum(i, j)][num] = true;}backtracking(0, 0);
}private boolean backtracking(int row, int col) {while (row < 9 && board[row][col] != '.') {row = col == 8 ? row + 1 : row;col = col == 8 ? 0 : col + 1;}if (row == 9) {return true;}for (int num = 1; num <= 9; num++) {if (rowsUsed[row][num] || colsUsed[col][num] || cubesUsed[cubeNum(row, col)][num]) {continue;}rowsUsed[row][num] = colsUsed[col][num] = cubesUsed[cubeNum(row, col)][num] = true;board[row][col] = (char) (num + '0');if (backtracking(row, col)) {return true;}board[row][col] = '.';rowsUsed[row][num] = colsUsed[col][num] = cubesUsed[cubeNum(row, col)][num] = false;}return false;
}private int cubeNum(int i, int j) {int r = i / 3;int c = j / 3;return r * 3 + c;
}
} 
51 .N皇后问题 
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 
     
上图为 8 皇后问题的一种解法。 
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。 
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 
   
class Solution {private List> solutions;
private char[][] nQueens;
private boolean[] colUsed;
private boolean[] diagonals45Used;
private boolean[] diagonals135Used;
private int n;public List> solveNQueens(int n) {solutions = new ArrayList<>();nQueens = new char[n][n];for (int i = 0; i < n; i++) {Arrays.fill(nQueens[i], '.');}colUsed = new boolean[n];diagonals45Used = new boolean[2 * n - 1];diagonals135Used = new boolean[2 * n - 1];this.n = n;backtracking(0);return solutions;
}private void backtracking(int row) {if (row == n) {List list = new ArrayList<>();for (char[] chars : nQueens) {list.add(new String(chars));}solutions.add(list);return;}for (int col = 0; col < n; col++) {int diagonals45Idx = row + col;int diagonals135Idx = n - 1 - (row - col);if (colUsed[col] || diagonals45Used[diagonals45Idx] || diagonals135Used[diagonals135Idx]) {continue;}nQueens[row][col] = 'Q';colUsed[col] = diagonals45Used[diagonals45Idx]= diagonals135Used[diagonals135Idx] = true;backtracking(row + 1);colUsed[col] = diagonals45Used[diagonals45Idx] = diagonals135Used[diagonals135Idx] = false;nQueens[row][col] = '.';}
}
} 
======土哥的升级服务======= 
如果你因为找工作而烦恼，不会做简历，不会备战复习，不会面试技巧，不会 HR 面，不会谈薪，不用怕，有土哥。 
土哥社招参加 28 场面试，100% 通过率，拿到全部 offer！ 
土哥这半年的悲惨人生，经历过被鸽 offer,最终触底反弹~ 
你可以找土哥修改简历，1 对 1 辅导项目、面试技巧，HR 面以及谈薪等，同时发你总结的最新面经试题（有偿哈），具体价格私信土哥。备注：简历修改+面试辅导 
毕竟免费的东西，不仅你不会上心，土哥也没有多大精力认真去修改和辅导。 
当然，想进群的，也可以加土哥，备注：加群~ 
土哥V：youzhiqiangshou_02
                        
                        
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！



                    



                    

    收藏
    



                    
    
        
        标签：技术
        
    

    
        
                
            上一篇 >
            InGaAs短波红外探测器未来发展趋势
        
                
            下一篇 >
            【力扣】刷题，手写Java算法，每日一题，持续更新...
        
                
    



                    
    
        
        
            相关文章
        
                
            Duilib中list控件支持ctrl和shif多行选中的实现
        
                
            [ICML2015]Batch Normalization:Accelerating Deep Network Training by Reducing Internal Covariate Shif
        
                
            win10系统 微软输入法 于eclipse ctrl+shif+f冲突间接处理办法
        
                
            Codeforces Round #259 (Div. 2) B. Little Pony and Sort by Shif
        
                
            读LDD3，内存映射与DMA--PAGE_SHIF…
        
                
            VMware虚拟机安装XP【要先分区，再设置BOOT 启动CD，shif+上移】
        
                
            更换iBus五笔的左与右Shif
        
                
            sublime ctrl+shif+f 没用解决办法
        
                
            idea 对 ctrl + z 的撤销 是 ctrl + shif + z
        
                
            计算机最早的设计师应用于,计算机应用基础选择题doc.doc
        
                
            win10自带截图神器：Win+Shift+S
        
                
            Python基础之文件目录操作
        
                
            python简述目录_Python基础之文件目录操作(示例代码)
        
                
            tp5 如何做数据采集
        
                
            任务2-7(服务器字体+阿里巴巴矢量库)
        
                
            html标签（1)：h1~h6,p,br,pre,hr
        
                
            TI 电量计介绍与芯片选型指南
        
                
            几款TI电源芯片简介
        
                
            TI DSP芯片C2000系列读取FLASH数据
        
                
            德州仪器(Ti)平台嵌入式开发基础
        
                
            TI三相电机智能栅极驱动芯片特点分类
        
                
            省选模拟（12.08） T3 圈圈圈圈圈圈圈圈
        
                
            Hadoop生态圈技术栈（上）
        
                
            大数据开发基础入门与项目实战（三）Hadoop核心及生态圈技术栈之6.Impala交互式查询
        
                
            小猿圈之Linux下Mysql 操作命令
        
                
            大数据Hadoop生态圈常用面试题
        
                
            大数据开发基础入门与项目实战（三）Hadoop核心及生态圈技术栈之4.Hive DDL、DQL和数据操作
        
                
            备战Noip2018模拟赛11（B组）T3 Monogatari 物语
        
                
            【智能优化算法-圆圈搜索算法】基于圆圈搜索算法Circle Search Algorithm求解单目标优化问题附matlab代码
        
                
            NYOJ 78 圈水池
        
                
            递归问题 跑道 汽车 绕圈问题 Python实现
        
                
            Hadoop生态圈（三）：MapReduce



        
            


            

    
        内容推荐
    
    
                
            
                1
            
            
                大厂出品！保姆级教程帮你掌握「用户体验要素」
            
        
                
            
                2
            
            
                大厂实战案例！设计师如何助力京东快递业务增长？
            
        
                
            
                3
            
            
                总监干货！5个常见的UI设计规范创建误区
            
        
                
            
                4
            
            
                数据库管理利器——Navicat Premium v17.0.4学习版(Windows+MacOS+Linux)
            
        
                
            
                5
            
            
                进阶必学！快速掌握10种国际主流设计模型
            
        
                
            
                6
            
            
                春节期间，10个大厂的产品细节走心设计
            
        
                
            
                7
            
            
                如何帮助用户度过新人期？来看雪球APP的实战总结！
            
        
                
            
                8
            
            
                Sketch 95.3最新版下载 (Sketch矢量绘图应用软件)
            
        
                
            
                9
            
            
                Axure RP 9 最新正式版安装软件与汉化语言包下载(2023年3月30日更新)
            
        
                
            
                10
            
            
                嘘！SaaS产品的差异化设计细节，一般人我不告诉他
            
        
            




    





    
    
        最新更新
    
    
        
                        
                [产品经理]
                3分钟绘制流程图！这个AI+绘图工具的神仙组合，学完老板直呼内行
            
                        
                [产品经理]
                商业潜规则：打败你的不是AI，而是人性
            
                        
                [产品设计]
                DeepSeek+智能派单系统的实践分享
            
                        
                [产品经理]
                一文读懂本年实际损益借(贷)方发生额
            
                        
                [创业学院]
                大客户 vs 中小企业：需求竟天差地别？以企业培训数字化为例
            
                        
                [产品经理]
                不要将员工的“猴子”背到自己身上：职场管理中的权责划分
            
                        
                [产品经理]
                人工智能的三层架构：从应用层到基础服务层，解密智能革命
            
                        
                [产品设计]
                一文讲清楚iOS的SKAN4.0
            
                    
    
    



    
        热门标签
    
    
        
                         数量
                         AI技术趋势
                         用户角色
                         心智游移
                         自然生态系统
                         会员权益
                         AirDrop
                         hashmap
                         小龙虾
                         焦虑
                         危机处理
                         发展
                         微信群折叠
                         toast
                         测评新算法
                         改版
                         wireshark
                         投放方式
                         音频播放动效
                         timer
                         女性商业
                         古典自媒体
                         海外博主
                         repeater
                         转账
                         万能钥匙
                         秋招
                         快服务
                         个人演讲
                         客户共识