洛谷P1244 [NOI2000] 青蛙过河

题面：

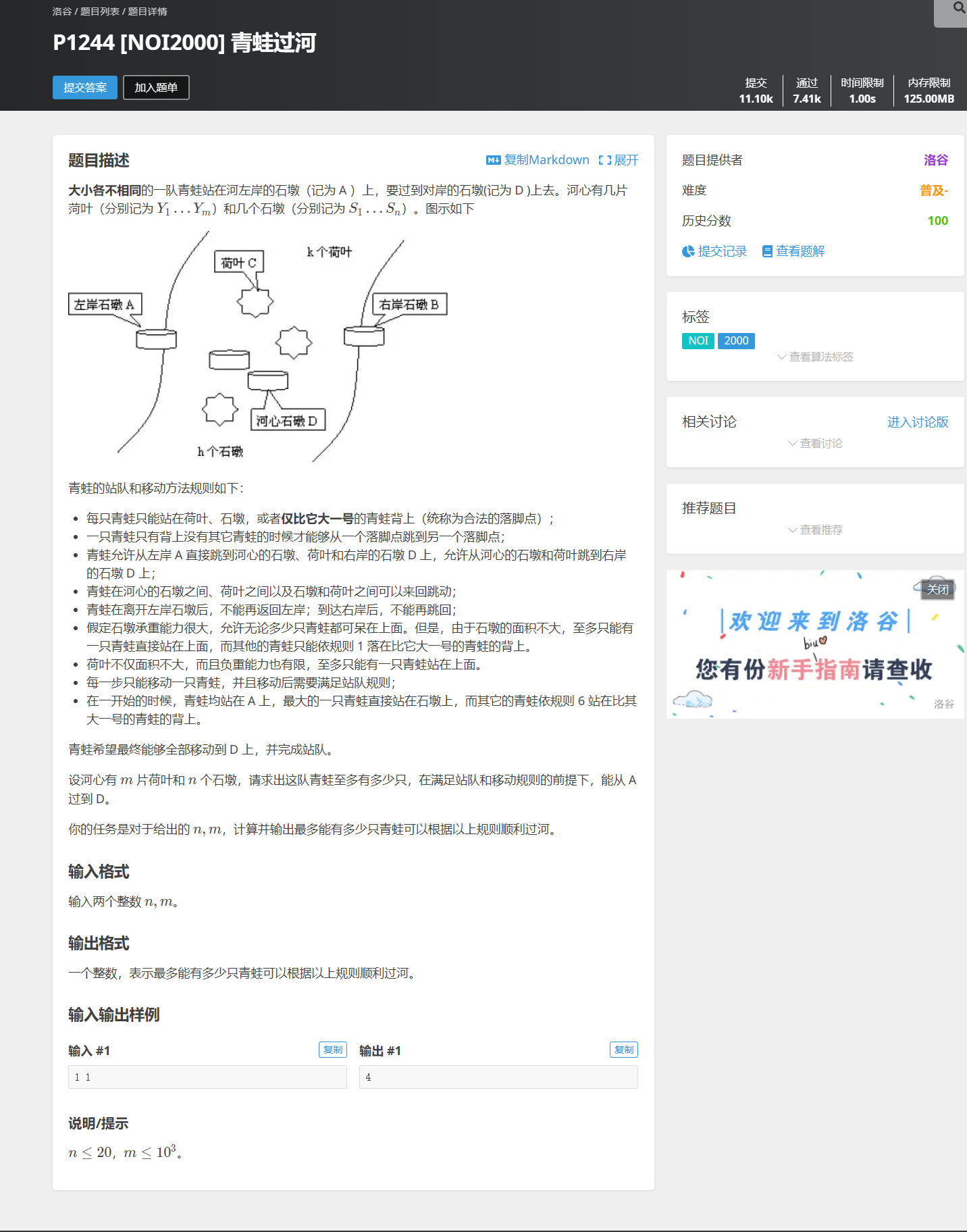
解题：

找规律！

当无法一眼望穿题目时，不妨拿起笔和纸，在纸上实现一些简单的模拟：

我们为每n青蛙分别挂上号码牌：1~n：

1. 石墩为0 （绿色荷叶，紫色青蛙）

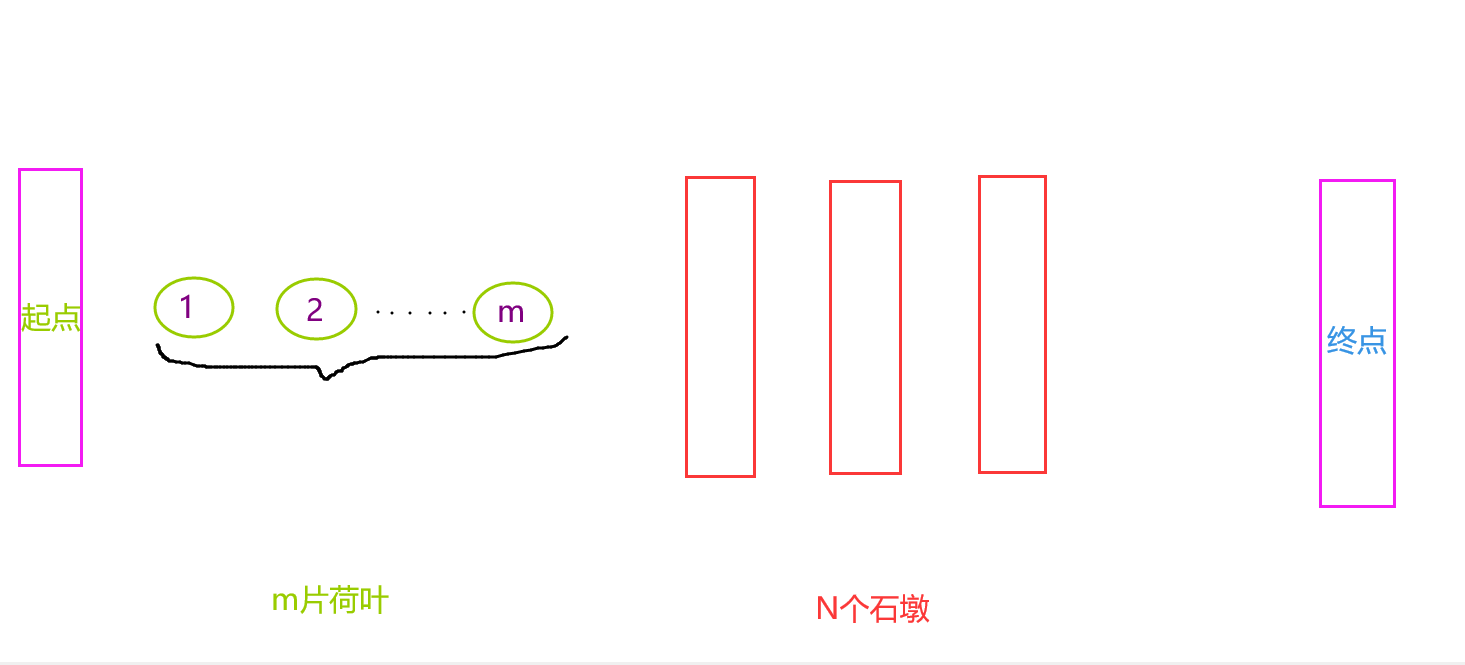
请看下图：1~m号青蛙全部跳到了m片荷叶上！

因为荷叶只能称重一只青蛙，因此，石墩为0时，

第m+1只青蛙只好跳向对面的终点，再让1~m号依次跳到自己背上

固n=1时，最大青蛙数为：m+1

2. 石墩为1

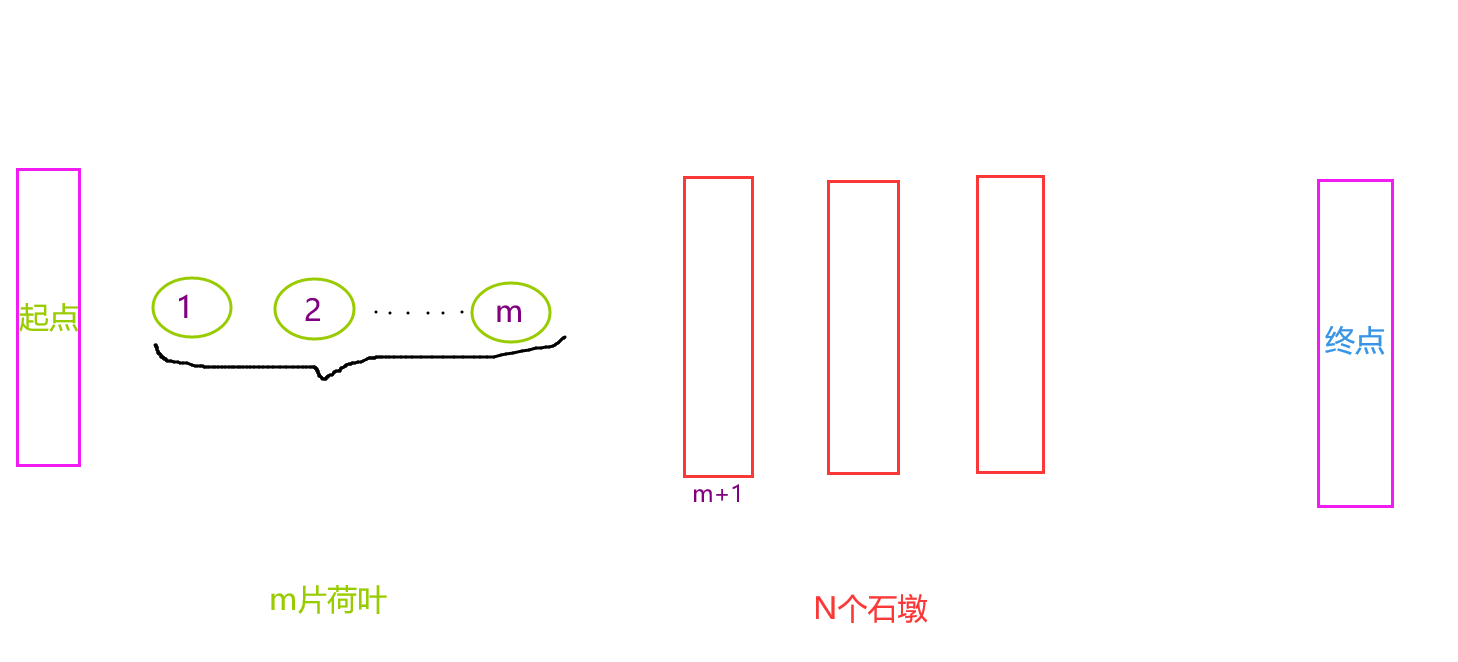
与n=0相比，情况发生了变化：

在1~m号青蛙跳到荷叶上时，第m+1青蛙勇敢地跳向唯一的石墩，这使得1~m号青蛙得以跳到其背上，释放出m片荷叶给m+2~2m+1号青蛙！

如此，n=1时，最多能通过的青蛙数增加到了2m+2！

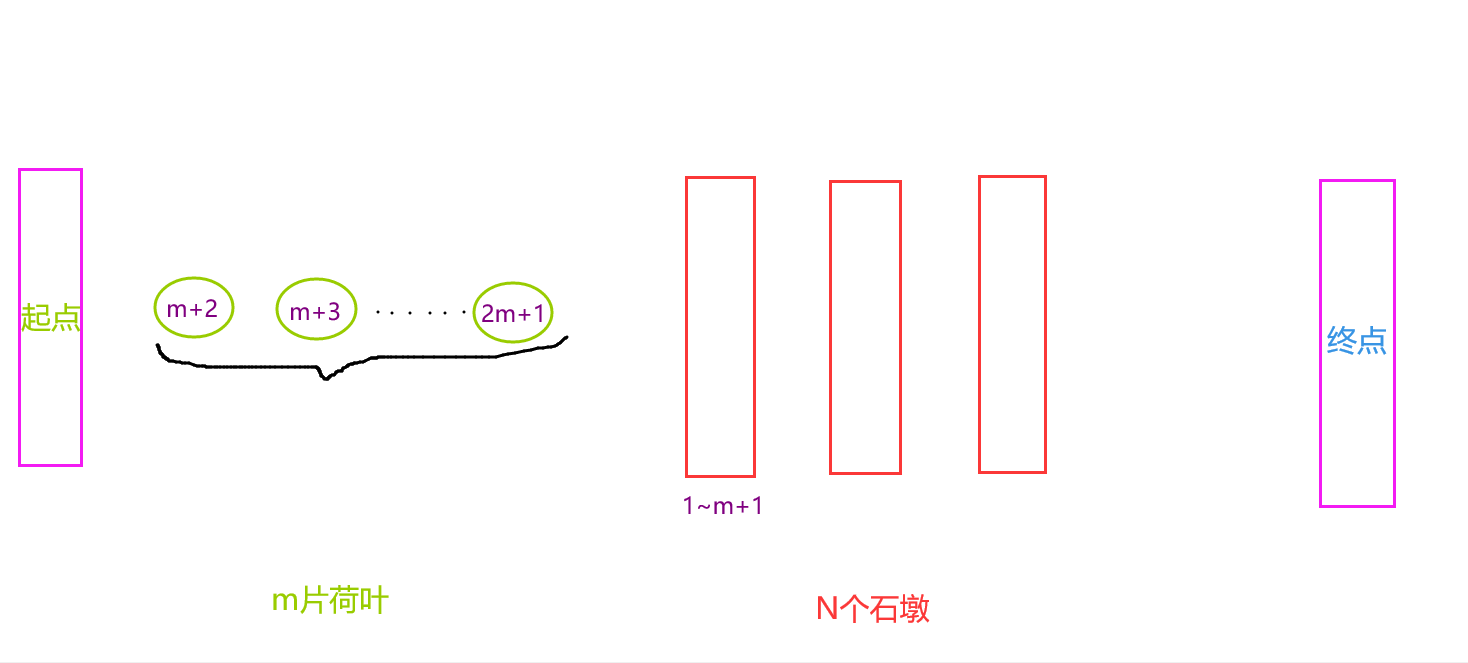
3. 石墩为2

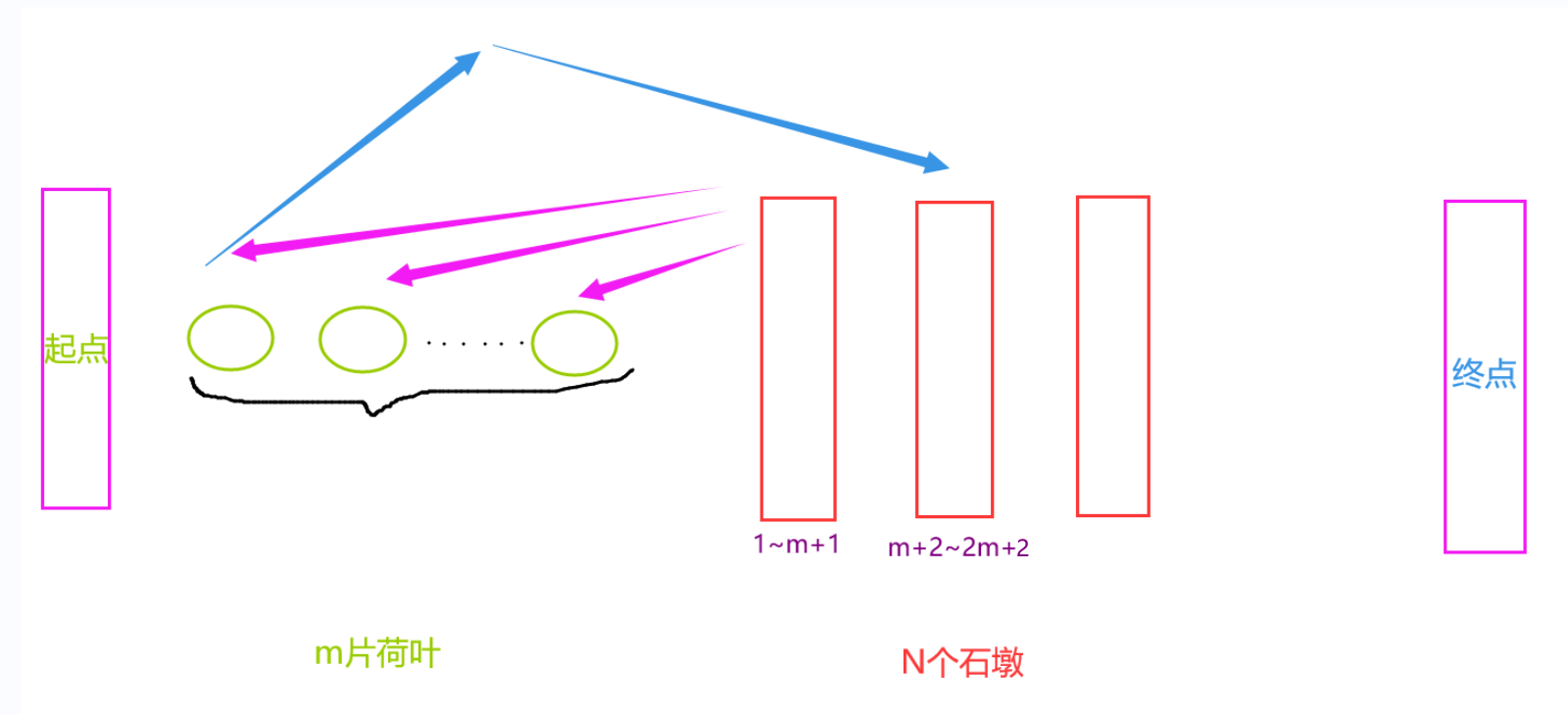
如果我们有2个石墩，那么青蛙的旅途就不会止步于2m+2啦！

如图，m+2~2m+2号青蛙又可以如法炮制地跳到第2号石墩上。

这时，不必急着将起点等候多时的2m+3~3m+2青蛙放到荷叶上，

我们发现了更优解：将1~m号转移到荷叶上，再转移到2号石墩上，释放出了1号石墩！

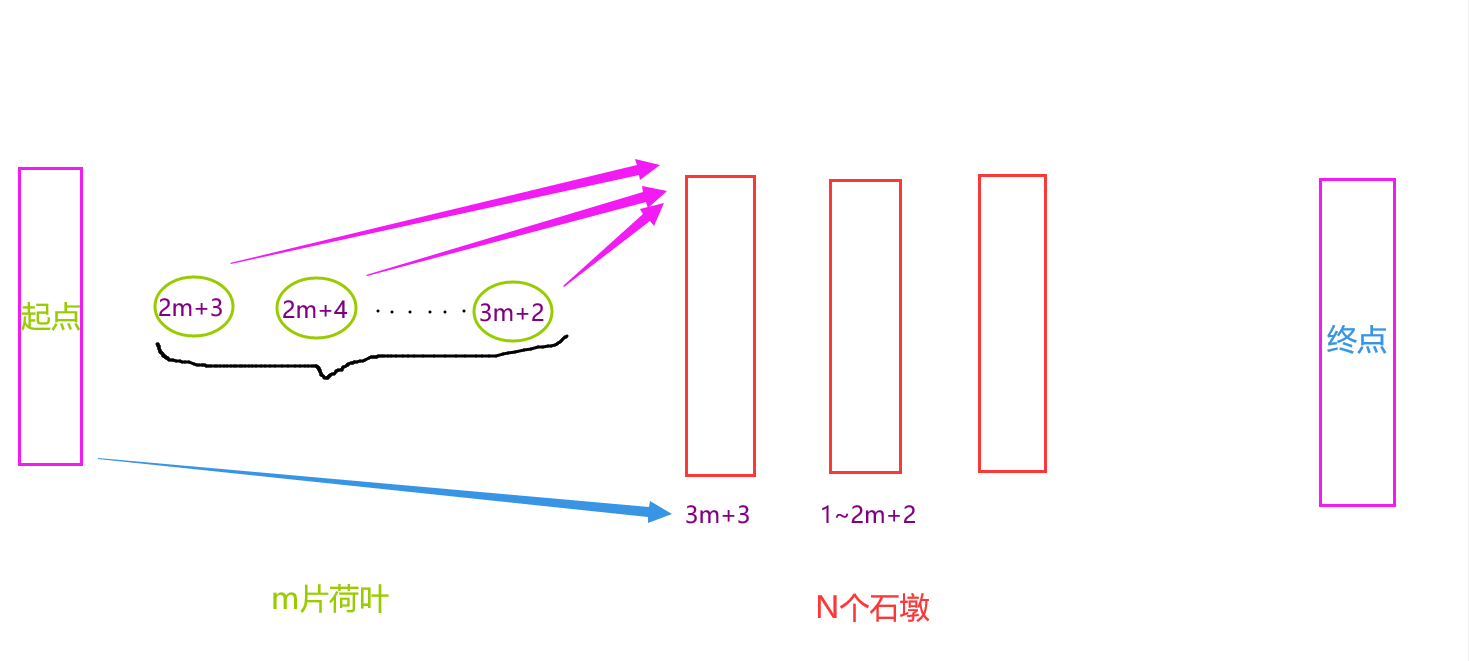
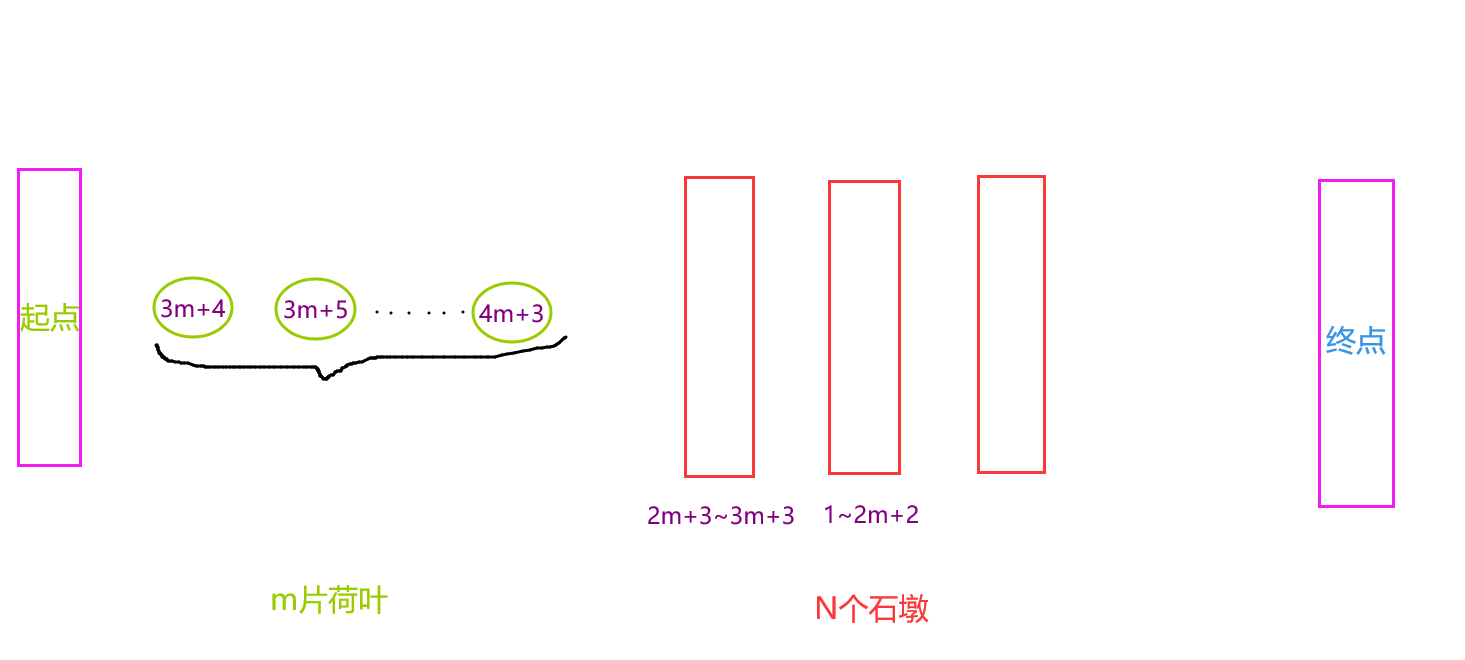
此后，2号石墩上的1~2m+2号青蛙固定，于是，情境又变回只有一个石墩。

我们简单地模拟，或者直接将2号石墩上的2m+2 加上 n=1时的最多青蛙数：“2m+2”后，

得出了无可争议的，n=2时的答案：4m+4！

n=0 ans=m+1

n=1 ans=2m+2

n=2 ans=4m+4

聪明的你一定早就发现规律了吧！ 这次，我用找规律水过了dp（嘻）

可以自信地推出：答案ans=（m+1）* 2^n

AC代码奉上：

#include
#include
#includeusing namespace std;int n, m, ans = 0;       //m片荷叶、n个石墩
int a[1005] = { 0 }; //荷叶：1~1000
int b[25] = { 0 };   //石墩：int main()
{cin >> n >> m;ans = n + m + 1;    //至少(m+n+1)只可以成立ans = max(ans, (1 << n) * (m + 1));cout << ans << endl;return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！