牛顿法与梯度下降法

牛顿法与梯度下降法

martin

• 牛顿法与梯度下降法
  • 牛顿法与梯度下降算法的适用范围
  • 牛顿法
    • 一元函数二阶逼近
    • 多元函数二阶逼近
  • 梯度下降法

---

牛顿法与梯度下降算法的适用范围

• 这两种算法都只能找到局部最小值，也就是说容易陷入局部最优。
• 两种算法都必须给出一个初始点。
• 牛顿法使用二阶逼近，梯度下降法使用一阶逼近。
• 牛顿法对局部凸的函数能找到极小值，对局部凹的函数能找到极大值，对局部不凸不凹的可能找到鞍点。
• 梯度下降法一般不会找到最大值，但同样可能会找到鞍点。
• 当初始点选取合理的情况下，牛顿法比梯度下降法收敛的速度快。
• 牛顿法要估计二阶导数，计算难度相对要大。

牛顿法

一元函数二阶逼近

首先在初始点$x_0$处写出二阶泰勒级数：

$$f(x_0+\Delta x) = f(x_0)+f^{'}(x_0)\Delta x+{f^{''}(x_0)\over 2}\Delta x^2+o(\Delta x^2) = g(\Delta x)+o(\Delta x^2)$$
我们知道关于 $\Delta x$的二次函数 $g(\Delta x)$的极值点为 $-{f^{'}(x_0)\over f^{''}(x_0)}$，(可以类比二次函数， $y = ax^2+bx+c$，它的极值点坐标为 $-{b\over 2a}$),那么本着逼近的精神 $f(x)$的极值点估计在 $x_0--{f^{'}(x_0)\over f^{''}(x_0)}$附近，于是定义 $x_1 = x_0--{f^{'}(x_0)\over f^{''}(x_0)}$，并重复此步骤得到此序列：
$$x_{n+1} = x_n-{f^{'}(x_n)\over f^{''}(x_n)}$$

多元函数二阶逼近

如果函数$f(x)$是一个多元函数，$x$是一个向量，那么牛顿法序列变为：
$$x_n+1 = xn - (\mathbb{H}f(x_n))^{-1}.\nabla f(x_n)$$
思路与技巧完全相同，只是使用梯度$\nabla f(x_n)$取代一阶导数$f^{'}(x_n)$，使用Hessian矩阵$\mathbb{H}f(x_n)$代替二阶导数$f^{''}(x_n)$。

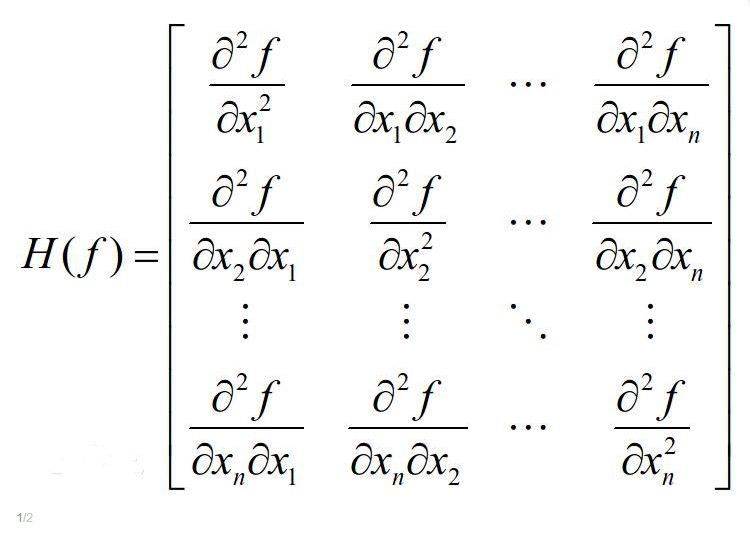
梯度下降法

参考我之前写的文章：http://blog.csdn.net/ice_martin/article/details/60972131

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！